What SI unit and common variables are associated with length?
Length or distance has SI units of meters (m).
The variables d and x are used for distance, h for height, z for depth, and r for radius.
What SI unit and common variables are associated with time?
Time has SI units of seconds (s).
The variable t is used for time, T is used for period and also has SI units of seconds.
What SI unit and common variables are associated with area?
Area has SI units of meters2(m2).
The variable A is used for area, S is used for surface area.
What SI unit and common variables are associated with volume?
Volume has SI units of meters3(m3).
The variable V is used for volume.
What SI unit and common variables are associated with velocity?
Velocity or speed has SI units of meters/second (m/s).
The variable v is used for velocity (a vector), though rarely used, s may be used for speed (magnitude only, scalar).
What SI unit and common variables are associated with acceleration?
Acceleration has SI units of meters/second2(m/s2).
The variable a is used for acceleration (a vector).
What two characteristics are necessary to define a vector?
Magnitude and direction.
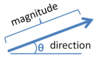
Define:
magnitude of a vector
Magnitude is the quantity, size, or amount and is a scalar value since it lacks direction.
Define:
direction of a vector
Direction provides spacial orientation, angle, or path.
By convention, two perpendicular directions are fixed as positive (right and up) and their opposites as negative (left and down).
What is the magnitude of the velocity vector pointing directly down at 5 m/s?

5 m/s.
Magnitude is the quantity, size, or amount.
What is the direction of the velocity vector pointing directly up at 13 m/s?

Directly upwards.
Direction is the angle, orientation, or path.
Describe the general process for vector addition.
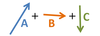
Vectors are added “tip to tail” so that there is a continuous pathway formed from the first arrow through the last one.
The sum vector is made by connecting the original tail to the final tip.
Describe the general process for vector subtraction.
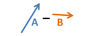
Vectors are subtracted in the same process as addition: “tip to tail”. The direction of the vector being subtracted must be reversed prior to adding.
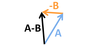
Define:
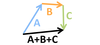
component vectors
Component vectors represent the magnitude of a given vector along the x axis and y axis.
Generally these are referred to as, for instance, the “x component of [vector]”. In the image below, vector A is shown with its x and y components as Ax and Ay respectively.

Give the formula for the x component of a force in the xy plane.
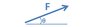
Fx = F * cos θ

In general: [vector]x = [original vector] * cos θ
What is the x component of velocity for a ball thrown upwards at 4 m/s, 30º to the horizon?
(sin(30º) = .5, cos(30º) = .86)

3.4 m/s
vx = 4*cos (30º)
= 4 (.86)
= 3.4 m/s
Give the formula for the y component of a force in the xy plane.

Fy = F * sin θ
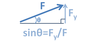
In general: [vector]y = [original vector] * sin θ
What is the y component of velocity for a ball thrown upwards at 4 m/s, 30º to the horizon?
(sin(30º) = .5, cos(30º) = .86)

2 m/s
vy = 4*sin (30º) = 4 (.5) = 2 m/s
Define:
instantaneous velocity (vo).
Instantaneous velocity is the direction and magnitude of the rate of change of displacement (or position) per unit time.
vo = Δx / t
or: vo = p/m
Where p is the object’s momentum and m is its mass.
Give the instantaneous velocity for a 3kg block with a momentum of 12kg*m/s.
4m/s
From p = mv, 12 = 3(v), v = 4m/s.
Define:
average velocity (vave)
Average velocity is the total distance and direction traveled from an initial position, divided by the total time.
vave = Δxtotal / Δttotal
or: vave = (vf + vi)/2
Note: the second equation assumes constant acceleration, which is also assumed on the AP exam unless specified otherwise.
Give the average velocity for a 1kg block after falling from rest for 2 seconds.
9.8 m/s
From: v = (1/2)at2
vf= (1/2) (9.8) (2)2 = 2 (9.8)
= 19.6 m/s and given: vi = 0.
From vave = (vf + vi)/2
vave = (19.6 + 0)/2 = 9.8 m/s
What formulas can be used to find final velocity, if given initial velocity?
vf = vi + at
or: vf2 = vi2 + 2aΔx
Where:
vf = final velocity in m/s
vi = initial velocity in m/s
a = acceleration in m/s2
Δx = displacement in m
t = time in s
Give the velocity of a 1kg block after falling for 2 seconds from rest.
19.6 m/s
From: vf = vi + at
vf= 0 + (9.8)(2) = 2(9.8)
= 19.6 m/s
Define:
acceleration
Acceleration is the rate at which velocity changes per unit of time.
a = Δv / t
What must have happened to the value of acceleration, if the same change in distance is now traveled in 1/2 the time?
4x the acceleration.
Since a is proportional to Δx/t2, halving t will quadruple a.
What is the acceleration always associated with an object in free fall?
9.8 m/s2
This is the acceleration due to gravity, commonly called g. On the AP exam, any falling object is assumed to be in free fall (no air resistance) unless told otherwise.
Note: while it’s convenient to use 10 m/s2 for calculations, the AP exam expects you to still choose the correct answer mathematically.
How is the maximum height of an object in projectile motion found?
The maximum height of an object in projectile motion can be found by finding the point where the vertical component of velocity, vy, equals zero. Then input this value into the equation with distance, to solve.
The object moves upwards until it reaches this point, and then starts moving downwards.
What is the maximum height of a ball thrown directly upwards from the ground with a velocity of 10 m/s?
The ball’s maximum height is 5m.
The kinematic equation that most easily solves this question is
vf2 = v02 + 2aΔx
Setting v0 to 10m/s, vf to 0m/s, and a to -10m/s2 yields:
0 = 100 + 2(-10)Δx
Δx = 5m
Define:
air resistance
Air resistance is the frictional force that opposes an object moving in free fall.
Fair = -kv2
The force of air resistance is proportional to the square of the velocity of the object falling. The constant k is a function of the object’s shape and surface area.
What is the corresponding change in magnitude of the force of air resistance if an object’s speed doubles?
(assume k remains constant)
Air resistance increases by 4x.
Since Fair is proportional to -v2, doubling velocity will quadruple the force. Recall that the negative sign only applies to direction and not magnitude.
Define and give units for:
Force
Force is the change in velocity per unit time that a given mass is experiencing. Force can also be thought of as the change in momentum per unit time.
The SI unit of force is the Newton (N),
1N = 1 kg*m/s2
What must be done to momentum, for an object to suddenly experience twice as much force on it?
Momentum per unit time must be doubled.
Since force is the change in momentum per unit time, these are directly proportional.
Describe Newton’s first law of motion.
aka the Law of Inertia: An object in motion will continue with constant velocity unless acted on by a net force.
Similarly, an object at rest will continue to remain at rest until acted on by a net force.
What must be true about the acceleration of an object, if all forces acting on it cancel?
The object has zero acceleration.
Since all forces cancel to be zero, there is not a net force and there will not be a change in velocity. If there is no change in velocity, that is the same as no acceleration.
What is the relationship between force, mass, and acceleration in Newton’s second law of motion?
Fnet = ma
Note: net force and acceleration are both vectors, and must be pointing in the same direction.
What is the proportional change in force to make an object move with twice its original acceleration?
Twice the original force must be applied.
From Newton’s second law, F=ma. Force and acceleration are directly proportional.
How does Newton’s third law of motion describe the forces between two objects?
F1on2 = -F2on1
For every force from one object on a second, there is an equal and opposite force from the second back on the first.
What magnitude of force must exist from apple to an orange in free space, if it’s found that there is a force from the orange to the apple of 5N.
5N
From Newton’s third law, every force excerted must have an equal and opposite force. The negative sign is already factored in, since the question specified direction.
What is the formula for gravitational force?
Fg = Gm1m2 / r2
Where:
G = gravitational constant in N*m2/kg2
m1 and m2 = masses in kg
r = distance between masses in m
What is the proportional change in gravitational force between two objects, if the distance between them doubles?
Force is decreased to 1/4.
Since F is proportional to 1/r2, doubling r will reduce the force by a factor of 4.
What is the proportional change in gravitational force between two objects, if the distance between them halves and each object’s mass also halves?
No change in force.
Since each mass is directly proportional to F, halving each mass will result in 1/4 the original F. But, since F is proportional to 1/r2, halving r will result in 4x F. The net change in F is the product both factors: 4(1/4) = 1, no change.
What is the more convenient relationship for force on a mass, due to gravity on Earth?
F = mg
Where:
F = force in N
m = mass in kg
g = acceleration due to gravity (9.8 m/s2)
What is the magnitude of the force acting downward on an apple with mass .2kg on Earth?
2N.
F = mg = .2(9.8) ≈ 2N
Note: if the apple is resting on the ground, it will also be subject to an equivalent normal force pointing upwards.
Define:
Weight
Weight is explicitly the force on an object due to gravity. W=mg
Weight if often confused with mass; an object with one weight on Earth will have a different, lesser, weight on the moon, but its mass will remain constant.
What will the proportional weight of an object be on the moon, if the moon has 1/6 Earth’s gravity?
The object will have 1/6 the weight it had on Earth.
Since W is proportional to the acceleration due to gravity, the moon’s lesser gravity will produce a proportionally lesser weight.
How could an object’s perceived (or instantaneous) weight seemingly change?
Perceived (or instantaneous) weight is the force pushing back on an object against gravity. This is a specific type of normal force.
A person might experience a decreased instantaneous weight if the ground falls away beneath them, such as if an elevator accelerated downwards.
How will a person’s instantaneous weight change if the elevator they are standing in begins to accelerate upwards?
Instantaneous weight while accelerating upwards will be greater than at rest, as the acceleration upwards adds to the normal force that the person experienced while at rest.
If the elevator had accelerated downwards, the person would feel less weight. In fact, if the elevator could accelerate downwards at 9.8m/s2 the person would experience weightlessness.
Define:
Normal force
When two objects are touching, there exists an opposing force between the two objects and perpendicular to the surface in contact. This is the normal force.
Often, on the AP exam, normal force is opposing the force due to gravity.

What is the normal force for a book of mass .5kg sitting stationary on a table?
5N directed towards the book, from the table.
The force pulling down on the book due to gravity is F = mg = (.5)10 = 5N downwards towards the table. Since the book is stationary, we know that normal force is equal and opposite; hence it must also be 5N in magnitude.
What is the relationship between normal force and friction for a static object?
Static friction (or rolling friction) is a force that opposes any two surfaces in contact from sliding over each other.
fs ≤ μsFN
Where:
fs = force of static friction in N
μs = coefficient of static friction
FN = normal force in N
Describe what would happen to a box, if a person pushed directly horizontally on the box with a force of:
- 1/2 μsFN
- μsFN
- 2μsFN
- No motion. 1/2 μsFN will be exerted back by static friction.
- No motion. μsFN will be exerted back by static friction.
- Accelerate forward and begin sliding. 2μsFN is greater than the maximum μsFN force that static friction can resist motion with.
What is the relationship between normal force and friction for a sliding object?
Kinetic friction (or sliding friction) is a force that opposes the motion of two surfaces sliding across one another.
fk = μkFN
Where:
fk = force of kinetic friction in N
μk = coefficient of kinetic friction
FN = normal force in N
Describe what would happen to an already sliding box, if a person continued pushing horizontally on the box with a force of:
- 1/2 μkFN
- μkFN
- 2μkFN
- Eventually come to rest. 1/2 μkFN is less than the force of kinetic friction acting against the box, so friction will slow the box.
- Continue sliding at constant v. μkFN will exactly cancel the force of kinetic friction against the box.
- Accelerate forward. 2μkFN is greater than the force of kinetic friction acting against the box.
Why is there an equals sign for the force of kinetic friction, but an inequality for the force of static friction?
Kinetic friction only depends on the composition of the two moving surfaces in contact, hence will be one value.
Static friction opposes any amount of force applied while the object remains immobile, hence its value can vary from zero up to the maximum for those surfaces.
In which of the following scenarios is static friction between the surfaces higher than kinetic friction?
- A brick on ice
- A brick on asphalt
- An ice block on glass
- An ice block on rubber
All of them. Static friction is always higher than kinetic friction for any pair of surfaces in contact.
Corollary: it always takes more force to start an object sliding than it does to keep it sliding.
What formulas give the component forces for the force due to gravity on an inclined plane?
(note that by covention the “x” axis is along the slope of the plane, and the “y” axis is perpendicular to the plane)

Fx=mg sinθ
Fy=mg cosθ
Since these are opposite from how we normally compute components, a way to remember the x component is: sine is for slope.

What calculation will give you the normal force on a box of mass m, on an inclined plane with angle θ?

FN = -mg cosθ

Since the box is not sinking into the slope, nor launching up off of the slope, the net force acting perpendicular to the slope must be zero. Hence, Fy=-FN
What is the force of static friction, if the box does not start to slide down the plane?

Fs = -mg sin(θ)

There are two forces parallel to the slope of the plane; the component of gravity parallel to the plane, with magnitude mg sin(θ), and the force of static friction, pointing in the opposite direction.
These forces must be equal and opposite to prevent motion.
In the pulley system demonstrated below, m2 is twice the mass of m1 and there is no net movement. What is the relationship between the tension in the string at points 1 and 2?

The tensions are equal.

A key to all pulley questions is to remember that the tension in the string running through the system is always constant, since it is all one string.
What is the force F in the pulley apparatus below, with respect to the mass m1, assuming that all masses are stationary and no friction exists?

F = m1g

There are two forces acting on m1; gravity and tension. If the box isn’t moving, they must be equal and opposite, so T = -m1g. Since tension is constant through the string, the force on m2 from tension must also be F = -T = m1g.
What is the force F in the pulley apparatus below, with respect to the mass m2, assuming that all masses are stationary and no friction exists?

F = -m2g sinθ

There are two forces acting on the box along the inclined plane: the x component of gravity and the tension in the string. If the box isn’t moving, they must be equal and opposite. Hence F = T = -m2g sinθ.
What is the formula for the centripetal acceleration acting on a body following a circular path with a constant speed v?
a = v2/r
On the AP exam, all circular motion occurs at a constant speed.
How does the acceleration experienced by a child on a merry-go-round change if the speed of the merry-go-round doubles?
The velocity increases by a factor of 4.
Since acceleration is proportional to the velocity squared, if the velocity doubles, the acceleration increases by the square of that amount, or 4x.
What is the centripetal force F experienced by a body traveling in a circle of radius r at a constant speed v?
F = mv2/r
This comes from F = ma, where a is the centripetal acceleration.
Where:
v = velocity in m/s
a = acceleration in m/s2
m = mass in kg
r = radius of circle in m
How does the centripetal force on objects 1 and 2 differ, if both are traveling the same circular path at the same speed, but object 2 is twice as heavy as object 1?
The centripetal force on object 2 (heavier) is twice that on object 1 (lighter).
Centripetal force is F = mv2/r. Since F is proportional to m, with all else equal, the force on the heavier object will be proportionally larger.
How does the centripetal force on objects 1 and 2 differ, if both are the same mass and traveling the same circular path, but object 2 is moving three times as quickly as object 1?
The centripetal force on object 2 is nine times that on object 1.
Centripetal force is F = mv2/r. Since F is proportional to v squared, with all else equal, the force on the heavier object will be larger by the square of the velocity difference.
Define:
a vector field
A vector field is a function that assigns a vector to every point in space.
The only common fields on the AP exam are force fields, which can be used to interpret the force an object at any given point in space will experience. Common examples are electric fields and gravitational fields.
What is the direction of the force experienced by an object placed at point A in the gravitational field depicted below?

The object feels a force down and to the left.

This is the direction the vectors in the vicinity of point A are pointing, and these vectors represet the forces experienced by objects at these locations.
On the AP exam, fields are assumed to be of uniform density until told otherwise.
Where is the magnitude of the field depicted below greater, point A or point B?

The magnitude of the field is greater at point B.

The magnitude of a field can be estimated from the density of the field lines in this location. The greater the density, the larger the magnitude of the field. The field lines are packed more tightly at point B than at point A, hence the magnitude of the field is greater there.
