Simple Harmonic Motion
- First, it always acts to restore the particle or object to its equilibrium position any time it is displaced. That is, the direction of the restoring force is always toward the equilibrium position.
- Second, the magnitude of the force is directly proportional to the magnitude of the displacement of the particle or object from its equilibrium position.
Springs
F=-kx (Hooke’s Law)
higher k=stiffer spring
Oscillating Systems

Angular Frequency
ω
- radians per second.
- **ω=2πf=√(k/m)=2π/T **
- where T is the period, 1/f (time to complete one cycle)
- measure of the rate at which the oscillating object would move through an arc of a particular size if the object were traveling around a perfect circle (for which one revolution around the circle equals one cycle).
- dependent on the spring constant and mass attached to the spring but not on the displacement x of the spring.
radians
180/π degrees
360 degrees = 2π radians
Equation for Position of a spring as it moves through its cycle as a funciton of time
x= X cos (ωt)
- X is the amplitude (maximum displacement from equilibrium), ω is the angular frequency (ω = 2π f = π /T, where T is the period, ,1/f the time to complete one cycle), and t is time*.
- assuming that the spring has maximum displacement at t = 0.
Springs as Conservative Systems
(2 conditions, 1 formula)
Conditions: 1) small oscillations, 2) short periods of time
[assume all the potential energy of the spring will be converted to kinetic energy as it oscillates.]
U=(1/2)kx2
K=(1/2)mv2
E=K + U = constant
Simple Pendulum
F= -mg sinθ
- where m is the mass attached to the end of the pendulum, g is the acceleration of gravity (9.8 m/s2), and θ is the angle between the pendulum arm and the vertical
- force equation has a negative sign, reminding us that this is a restoring force, always directed in the direction opposite to the displacement and in the direction of the equilibrium position.
Angular Frequency of a Pendulum (of length L)
ω= 2πf=√(g/L)
- NOTE: Neither the mass m attached to the pendulum nor the angular displacement θ determines the angular frequency ω
- Can change angular frequency by changing: length or gravity (ie elevator)
- <em>Therefore, if two pendulums have the same length, they will demonstrate the same angular frequency irrespective of the masses attached to them or their respective initial displacements. As with two identical springs stretched to different lengths with the same angular frequency but different linear velocities, the two pendulums will be traveling at different velocities.</em>
Pendulums as Conservative Systems
Neglect air resistance and friction and mechanism supporting pendulum above:
- When pendulum is pulled back to its maximum displacement θ, the pendulum has maximum potential energy (U) = mgh
- K=(1/2)mv2
-
E=K+U=constant
*
Comparing: mass-spring system and the simple pendulum

Frequency and Period
Frequency:
- f=ω/2π
- f=1/T
Period:
- T=2π/ω
- Wavelength*: λ=2π/k
- Speed*: v=fλ
Transverse Waves
- sinusoidal waves
- a waveform in which the direction of particle oscillation is perpendicular to the movement (propagation) of the wave
- the particles are oscillating perpendicular to the direction of energy transfer
- ie: Electromagnetic radiation

Longitudinal Waves
- sound waves
- particles of the wave oscillate along the direction of travel of the wave motion; that is, the wave particles are oscillating along the direction of energy transfer

Displacement (y) of a particle in a wave at a point (x)
y=Y sin (kx - ωt)
where Y is the amplitude (maximum displacement), k is the wavenumber (don’t confuse this k, wavenumber, with the spring constant k in Hooke’s law!), ω is the angular frequency, and t is the time.
speed of the wave (v)
v= (fλ) = (ω/k) = (λ/T)
because
v=fλ
k=2π/λ
ω=2πf=2π/T
f=1/T
Phase difference
Destructive (vs constructive) interference

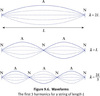
Traveling Wave

standing waves
Points in the wave that remain at rest (i.e., points where amplitude is constantly zero) are known as nodes, and points that are midway between the nodes are known as antinodes.
Antinodes are points that fluctuate with maximum amplitude.
The length of the medium dictates the wavelengths of traveling wave that are necessary for establishing the standing wave. Furthermore, the nature of the boundary dictates the appearance of a node or antinode at the boundary itself.
- Closed boundaries are those that do not allow oscillation and that support nodes. The closed end of a pipe and the secured ends of a string are both closed boundaries.
- Open boundaries are those that allow oscillation and support antinodes. The open end of a pipe and the free end of a flag are both open boundaries.
Natural Frequency
frequency or frequencies at which an object will vibrate when disturbed
forced oscillation
- If a periodically varying force is applied to a system, a system will then be driven at a frequency equal to the frequency of the force
- If frequency of the applied force is close to that of the natural frequency of the system, then the amplitude of oscillation becomes much larger.
- ie: parent pushing a child on a swing
Resonance
If the frequency of the periodic force is equal to a natural frequency of the system, then the system is said to be resonating, and the amplitude of the oscillation is at a maximum.
If the oscillating system were frictionless the periodically varying force would continually add energy to the system, and the amplitude would increase indefinitely.
Dampening
because no system is completely frictionless, there is always some dampening, which results in a finite amplitude of oscillation.
Sound
transmitted by the oscillation of particles along the direction of motion of the sound wave. Therefore, sound waves are longitudinal.
speed of sound
- inversely proportional to the square root of density
- directly proportional to the square root of the bulk modulus.
- As a result, sound travels fastest through a solid and slowest through a gas.
- The speed of sound in air at 0° C is 331 m/s.
audible waves
frequencies that range from 20 Hz to 20,000 Hz.
- infrasonic waves: Sound waves whose frequencies are below 20 Hz
- ultrasonic waves: frequencies are above 20,000 Hz
Intensity of a Sound (I)
I=P/A
- average rate per unit area at which energy is transferred across a perpendicular surface by the wave
- (Thus, Power delievered across a surface such as eardrum: P=IA)
- Proportional to the square of the amplitude **(doubling the amplitude produces a sound wave with 4 times the intensity)
- Intensity is inversely proportional to the square of the distance from the source. (Bc area of a sphere increases as a function of the square of the radius, sound waves transmit their power over larger and larger areas the farther from the source they travel. For example, sound waves that have traveled 2 meters from their source have spread their energy out over a surface area that is four times larger than that for sound waves of the same amplitude and frequency that have traveled 1 meter from their source)
Sound Level (β )
- β = 10 log (I/Io)
- where Io is a reference intensity set at the threshold of hearing, 1 × 10− W/m2
- decibels (dB)
Calculate new sound level:
βf = βi+ 10 log (If/Ii)
where (If/Ii) is the ratio of the final intensity to the initial intensity.

Pitch
our perception of frequency
Beats
What we hear if the two sound waves have nearly equal frequencies in the audible range, the resultant wave will have periodically increasing and decreasing amplitude,
fbeat = |f1-f2|
Doppler Effect
difference between the perceived frequency of a sound and its actual frequency when the source of the sound and the sound’s detector are moving relative to each other
- If the source and detector are moving toward each other, the perceived frequency f′ is greater than the actual frequency f,
- if the source and detector are moving away from each other, the **perceived frequency f′ is less than the actual frequency f. **
- f’=f[(v +/-vD)/ (v-/+ vs)
- where v is the speed of sound in the medium, vD is the speed of the detector relative to the medium, and vS is the speed of the source relative to the medium. The upper sign on vD and vS is used when the detector and the source are getting closer together. The lower sign is used when the detector and the source are going farther away from each other.
strings (standing waves)
λ=(2L)/n
- where n is a positive nonzero integer (n = 1, 2, 3,… )*
- Pattern: * etc.
From relationship that f=v/λ, the possible frequencies are:
f=(nv)/2L
where n is a positive nonzero integer (n = 1, 2, 3,… ).
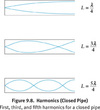
open pipes
λ=(2L)/n
- where n is a positive nonzero integer (n = 1, 2, 3,… )*
- Pattern:* etc.
From relationship that f=v/λ, the possible frequencies are:
f=(nv)/2L
where n is a positive nonzero integer (n = 1, 2, 3,… ).
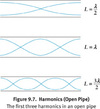
harmonic series
fundamental frequency( first harmonic): lowest frequency (longest wavelength) of a standing wave that can be supported in a given length of string
second harmonic: frequency of the standing wave given by n = 2 is known as the firstovertone or This standing wave has one-half the wavelength and twice the frequency of the first harmonic. All the possible frequencies that the string can support form its harmonic series.
The waveforms of the first three harmonics for a string of length L are shown.(Note: N stands for node and A stands for antinode.)
Closed Pipes
λ=4L/n
where n is odd integers only (n = 1, 3, 5,… ). The frequency of the standing wave in a closed pipe is f=nv/4L