자료구조 Flashcards
(43 cards)
AVL트리
정의: 편향트리일 경우 이진탐색트리(Binary Search Tree)의 탐색속도 저하되는 단점을 보완하기 위한 높이균형트리
#균형인수(Balance Factor(BF) : 왼쪽 서브트리의 높이 - 오른쪽 서브트리의 높이
>> AVL트리는 모든 노드의 균형인수가 =-1 이하
- BF > +-2 >> 4가지 방식으로 회전수행, 트리 전체를 재배열하지 않아도 균형유지(장점)
# AVL 트리에서 균형이 깨지는 경우 4가지 >> 회전(Rotation) 으로 자동으로 균형을 맞춤
- LL 타입 : Left 서브트리의 Left에 신규 노드 삽입 >> 경로상의 노드를 오른방향으로 회전
- RR 타입 : Right 서브트리의 Right에 신규 노드 삽입 >> 경로상의 노드를 왼쪽방향으로 회전
- LR 타입 : Left 서브트리의 Right에 신규 노드 삽입 >> 경로상 노드의 왼쪽방향 및 오른쪽반향 회전 수행
- RL 타입 : Right 서브트리의 Left에 신규 노드 삽입 >> 경로상 노드의 오른방향 및 왼쪽방향 회전수행
#응용분야: 이진탐색트리 사용분야 모두 가능, 컴퓨터 디렉토리 구조등의 계층구조

알고리즘 평가
알고리즘: 문제 해결을 위한 유한한 과정 또는 절차
#알고리즘 조건: 명확성, 효율성, 입력, 출력, 종결성
#평가요소
- 정확한 수행능력 : 실제 성능 측정
- 시간복잡도(Time Complexity) : 알고리즘 수행에 필요한 시간의 양
- 공간복잡도(Space Complexity) : 필요한 메모리의 양
- 단순성, 최적성, 작업량
#시간복잡도 점근(차츰점, 가까울근)표기법 >> 알고리즘 수행시간을 대략적으로 나타내는 방법
- 빅오(O) 표기법: 최악의 상황에서 보장되는 시간복잡도 >> 최고차 항으로만 표시, 최악의 경우에도 성능보장
- 빅오메가(Ω) 표기법: 최적의 상황에서의 시간복잡도
- 세타(θ) 표기법: 빅오와 빅오메가 시간복잡도의 중간
# 빅오(O) 표기법으로 표현한 알고리즘의 성능
- O(1) : 최악의 경우에도 일정한 상수 시간에 종료 > 해시테이블
# 공간복잡도
- Fixed Area : 프로그램 입출력 횟수나 크기와 관계없이 일정하게 필요한 공간
- Variable Area : 데이터의 개수에 따라 변하는 가변적인 공간

버블정렬 (Bubble Sort)
#정의: 나란히 있는 두개의 데이터를 계속 비교하여 교환하는 정렬하는 알고리즘 #정렬과정 - 1단계: list[i]와 list[i+1]를 i = 0,1,2, ···, n-2에 대하여 비교하여 만약 뒤 데이터가 값이 더 작으면 바꾼다 - 2단계: list[i]와 list[i+1]를 i = 0,1,2, ···, n-3에 대하여 비교하여 만약 뒤 데이터가 값이 더 작으면 바꾼다 - n-1단계: list[i]와 list[i+1]를 i = 0에 대하여 비교하여 만약 뒤 데이터가 값이 더 작으면 바꾼다 \>\> 이과정을 거치면 n-1 번째 큰 값이 뒤에서 n-1번째 위치하게 됨
/* list에 대한 기본 버블정렬 알고리즘 */
void bubble_sort(element list[], int n) {
int i, j;
element next;
for(i = n-1; i > 0; i–) {
for(j = 0; j < i; j++) {
if(list[j] > list[j + 1] {
swap(list[j], list[j + 1]);
}
}
}
}

삽입정렬 (Insert Sort)
정의: 데이터 집합을 순회하면서 정렬이 필요한 요소를 뽑아내어 이를 다시 적당한 곳에 삽입하는 정렬
- 1단계 : list[1]을 list[0]과 비교하여 만약 뒤 list[1] 데이터가 값이 더 작으면 바꾼다
(swap list[2]와 list[1]) >> 이 과정을 거치면 list[1], list[2]는 정렬된 상태가 된다. - 2단계 : list[2]을 list[1], list[0]과 순서대로 비교하여 만약 뒤 데이터가 값이더 작으면 바꾼다
(swap list[i]와 list[i+1]) >> dl 과정을 거치면 list[i], i = 0,1,2는 정렬된 상태가 된다. - 3단계 : list[3]을 list[i], i = 2,1,0 순서대로 비교하여 만약 뒤 데이터가 값이더 작으면 바꾼다
(swap list[i]와 list[i+1]) >> 이 과정을 거치면 list[i], i = 0,1,2,3은 정렬된 상태가 된다.
… - n-1단계 : list[n-1]을 list[i], i = n-2,n-3,…,2,1,0 순서대로 비교하여 만약 뒤데이터가 값이 더 작으면 바꾼다
(swap list[i]와 list[i+1]) >> 이 과정을 거치면 list[i], i = 0,1,2,3,…,n-1은 정렬된 상태가 된다.
/* 삽입정렬 – 데이터를 앞으로 이동하면서 끼워넣는다 */
void insertion_sort(element list[], int n) {
int i, j;
element next;
for(i = 1; i < n; i++) {
next = list[i];
for(j = i - 1; j >= 0 && next.key < list[j].key ; j–){
list[j + 1] = list[j];
};
list[j + 1] = next;
}

선택정렬 (Select Sort)
정의: 정렬이 안된 숫자들 중에서 최소값을 선택하여 배열의 첫번째 요소와 교환

퀵정렬 (Quick Sort)
정의: 분할과 정복(Divide and Conquer) 에 기반한 정렬알고리즘
#정렬과정
1. 피봇(기준값)을 선정하여 기준값보다 작은 요소는 왼편에, 큰 값은 오른편으로 분할시킴
2. 왼편과 오른편에서 다시 피봇을 선정하여 1의 과정으로 데이터 집합을 분할
3. 1,2과정을 하면서 더 이상 데이터집합으로 분할되지 않으면 정렬된 값을 얻게됨

퀵정렬 (Quick Sort)
/* 퀵 정렬 프로그램 */
void quicksort(element list[], int left, int right)
{
int pivot, i, j; element temp;
if(left < right) {
i = left; j = right + 1;
pivot = list[left].key;
do {
do i++;
while(list[i].key < pivot && i<=right);
do j–;
while(list[j].key > pivot);
if(i < j)
SWAP(list[i], list[j], temp);
} while(i < j);
SWAP(list[left], list[j], temp);
quicksort(list, left, j - 1);
quicksort(list, j + 1, right);
}
}

병합정렬 (Merge Sort)
정의: 리스트를 두개로 나누어 각각을 정렬한 다음 다시 하나로 합치는 정렬방법
#정렬과정
1. 정렬할 데이터 집합을 반으로 나눔
2. 나누어진 하위 데이터 집합의 크기가 2 이상이면 이 하위 데이터 집합에 대해 1번을 반복
3. 하위 데이터 집합들을 다시 병합하면서 집합의 원소를 정렬함
4. 데이터 집합이 하나가 될때까지 3번을 반복하면 정렬이 완료됨

힙정렬 (Heap Sort)
정의: 최대힙(내림차순 정렬), 최소힙(오름차순 정렬) 을 활용하는 정렬방법 O(n log n)

순차탐색
정의: 정렬되지 않은 배열의 항목들을 처음부터 마지막까지 하나씩 검사하여 원하는 항목을 찾아가능 방법
#자기구성 순차탐색: 자주사용하는 항목을 데이터 집합 앞쪽에 배치하여 탐색 효율 제고 방법
- 전진이동법(move to front) : 탐색되면 데이터 집합 가장앞(링크드리스트 헤드) 에 위치
- 전위법(Transpose) : 탐색된 항목을 바로 앞의 항목과 교환
- 빈도계수법(Frequency Count) : 탐색된 횟수를 별도의 공간에 저장> 높은순으로 데이터집합 재구성

이진탐색 트리
이진탐색트리 삽입과정 소스코드
#정의: 이진탐색과 같은 원리의 탐색구조이며, 비교적 빠른 시간안에 삽입과 삭제를 할 수 있는구조 # 이진탐색은 배열에 저장되어 삽입,삭제시 앞위의 원소를 이동시켜야 하는 불편함 있음. \>\> 삽입,삭제가 빈번히 이루어지면 반드시 이진탐색트리를 사용해야 함.
typedef struct _tagNode
{
Node* parent;
Node* left;
Node* right;
Int value;
} Node;
void InsertNode(Node*& treeNode, Node* newNode) {
if (treeNode == NULL) // 탐색이 실패한 곳의 부모 노드가 null 이면 루트에 삽입
treeNode = newNode;
else if (newNode->value < treeNode->value)
// 부모노드 키값보다 작으면 왼쪽에 삽입
InsertNode(treeNode->left, newNode);
else
InsertNode(treeNode->right, newNode);
}

해시테이블
해시 : 키값에 직접 산술적인 연산을 적용하여 항목이 저장되어 있는 테이블의 주소를 계산하여 항목에 접근
#해시테이블 : 값의 연산에 의해 직접 접근이 가능한 구조
#해싱: 해시테이블을 이용한 탐색
#해시의 용도: 해시테이블, 암호화, 데이터 축약
#해시함수
- 나눗셈법 : 주소=입력값%테이블크기(h(k) = k mod M)
- 자릿수 접기

해시충돌 해결기법
#해시충돌: 해시 함수가 서로 다른 입력값에 대해 동일한 해시 테이블 주소를 반환하는 현상 #개방주소법(Open Addressing) : 오버플로우 발생시 다른 데이터 주소로 다시 해시시키는 방법(반복 수행) #폐쇄주소법(Closed addressing) : 같은 데이터 주소내에서 끝까지 해결하는 방법 \>\> 체인법
체이닝
#정의: 오버플로우 발생시 링크드 리스트로 해결 #특징: 해시테이블은 링크드 리스트에 대한 포인터 관리

개방주소법
정의: 충돌 발생시 다른 주소를 사용할 수 있도록 허용하는 충돌해결 알고리즘
- 선형탐사(Linear Porbing): 충돌시 현재 주소에서 고정폭으로 다음 주소 이동
- 제곱탐사(Quadratic Probing) : 충돌시 이동폭이 제곱수로 이동
# 제곱탐사의 한계(2차 클러스터) : 같은 해시 값을 갖는 데이터에 대해서는 2차 클러스터 형성 문제
>> 클러스터를 제대로 방지할 수 있는 방법은 탐사할 주소의 규칙성을 없애는 것 - 이중해싱(Double Hashing) : 2개의 해시 함수를 준비해서 하나는 최초의 주소를 얻을때 사용하고 다른 하나는 충돌이 일어났을때 탐사 이동폭을 얻기 위해 사용
#재해싱: 해시테이블의 크기를 늘리고, 늘어난 해시테이블의 크기에 맞추어 테이블내의 모든 데이터를 다시 해싱

그래프
정의: 정점(Vertex)의 모음과 이 정점을 잇는 간선(Edge)의 모음간의 결합
#종류
- 무방향 그래프: (A,B) = (B,A)
- 방향성 그래프 : =/
- 가중치 그래프(Weighted Graph), 네트워크 : 간선에 비용이나 가중치가 할당된 그래프
#표시예
V(G1) = {0,1,2,3} , E(G1) = {(0,1), (0,3), (1,2) }, E(G2) = {<0,1>, <1,2>}

그래프 탐색
깊이우선탐색(Depth-Frist Search,DFS) : 더 나아갈 길이 보이지 않을때까지 깊이 들어가는 탐색
#DFS 탐색방법
1.시작 정점을 밟은 후 이 정점을 “방문했음” 으로 표시
2.인접정점중에 아직 방문하지 않은 곳을 선택하여 다시 깊이우선 탐색 시작
3.더 이상 인접정점이 없으면 이전정점으로 돌아와서 2번 수행
4.이전 정점으로 돌아가도 더 이상 방문할 이웃이 없으면 탐색 종료
#너비우선탐색(Breath Frist Search,BFS) : 꼼꼼하게 좌우를 살피면서 탐색하는 기법
#BFS 탐색방법
1. 시작 정점을 “방문했음”으로 표시하고 큐에 삽입(Enqueue)
2. 큐로부터 정점을 제거(Dequeue) 함. 제거한 정점이 이웃하고 있는 인접정점 중 아직 방문하지 않은 곳들을 “방문했음”으로 표시하고 큐에 삽입
3. 큐가 비게 되면 탐색 종료
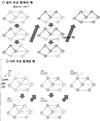
위상정렬
위상정렬

신장트리(Spaning tree)
정의: 그래프 내의 모든 정점들이 연결되어 있고, 사이클을 포함하지 않은 트리

최소신장트리
정의: 간선에 가중치 속성을 부여하여 각 간선이 갖고 있는 가중치의 합이 최소가 되는 신장트리
#대표적인 알고리즘 : Prim(프림) , Kruskal(크루스칼) 알고리즘
#특징
- 정점에 인접한 간선 중 가장 비용이 적은 간선은 반드시 최소비용신장트리에 포함된다
- 최소비용신장트리에 포함되는 간선으로만 이루어진 트리에서 외부에 있는 정점들을 잇는 모든 간선 중 가장 비용이 적은 간선은 반드시 최소비용신장트리에 포함됨.

프림(Prim) 알고리즘 O(e log e)
정의: 시작정점에서부터 출발하여 신장트리 집합을 단계적으로 확장하면서 최소신장트리를 작성하는 알고리즘
#최소신장트리 작성 순서
1. 그래프와 최소신장트리 준비
2. 그래프의 임의의 정점을 시작정점으로 선택하여 최소신장트리의 루트노드로 삽입
3. 최소신장트리의 정점들과 모든 인접정점 사이의 가중치가 가장 작은 것을 선택하여 이 간선에 연결된 인접정점을 최소신장트리에 삽입(이때 사이클이 형성되면 안됨.)
4. 3번을 반복하여 그래프의 모든 정점을 연결하게 되면 알고리즘 종료

크루스칼(Kruskal) 알고리즘 O(n^2)
정의: 그래프의 모든 간선의 가중치를 오름차순으로 목록을 만들어서 최소신장트리를 작성하는 알고리즘
#최소신장트리 작성 순서
1. 그래프 내의 모든 간선을 가중치의 오름차순으로 목록 작성
2. 목록을 차례대로 순회하면서 정점을 최소신장트리에 추가 ( 이때 사이클 형성되는 목록은 버림)
>> 탐욕 알고리즘 방식으로 처리됨

Sollin 알고리즘 O((n^2) log n)
정의: 각 단계(정점)에서 여러 개의 간선을 선택하여, 최소 비용 신장 트리를 구축
>> 현재 노드에서의 최단거리를 기준으로 선택함(프림과 기준은 동일)
#특징 : 가능한 최소한의 cost를 갖는 subset인 포레스트를 구성하고 포레스트간에 최소비용 정점으로 연결함
#프림과 다른점
- 프림은 시작정점을 선택하여 루트노드로 삽입
- 솔린은 간선을 모두 지운 정점들만의 숲에서 최소비용으로 간선을 연결하여 두개의 트리를 구성
>> 두개의 트리에서 최소비용 정점을 연결하면 완성

다익스트라 (Djkstra) 알고리즘
정의: 그래프 내의 한 정점에서 다른 정점으로 이동할때 가중치 합이 최소값이 되도록 만드는 경로를 찾는 알고리즘(최단경로) >> 경로의 길이를 감안해서 간선을 연결!
#특징: 하나의 시작 정점으로부터 모든 다른 정점까지의 최단 경로를 찾는 알고리즘
- Bellman-Ford 알고리즘 : 음의 가중치 허용한 경로까지 판단하는 최단경로 알고리즘
#최단경로 탐색 순서
1. 각 정점 위에 시작점으로 부터 자신에게 이르는 경로의 길이를 저장할 곳을 준비(모든 정점 위에 경로는 무한대)
2. 시작정점의 경로길이를 0으로 초기화하고 최단 경로에 추가
3. 최단경로에 새로 추가된 정점의 인접 정점들에 대해 경로 길이를 갱신하고 최단 경로에 추가
(추가하려는 인전정점이 이미 최단경로에 존재하더라도 갱신된 경로가 작으면 기존 경로를 현재 정점 경유로 수정)
4. 그래프 내의 모든 정점이 최단 경로에 소속될때까지 3번 반복
>> 1,2번은 사실알고리즘 초기화 작업
>> 3,4번은 최단경로를 찾는 탐욕알고리즘 방식( 해 선택, 실행가능성 검사, 해 검사)
( 해집합 : 최단경로, 부분문제 해는 각 정점 )


















