1.4 Valuation Flashcards
What is compounded interest?
Where we add the interest from each period to the principal so that it also accrues interest in the next period.
If one has value P today, invested at rate r for n years, what is the final value?
What is the difference between compounding and discounting?
Compounding: we take present value and calculate the future value.
If one receives value F for n years, discounted at rate r, what is the present value?
PV=F÷(1+r)^n
What do we normally do in discounting?
As it is usually regular inflows of payments, we sum the values of each individual year.
Baseline case: Certain cash flows, flat (time-invariant) discount rate.
What is the formula for calculating present value?
What are considered to be risk-free securities?
Why?
US
- Fiscal instruments - the power to tax the wealthiest population in the world.
- Ability to print money - will always be able to fulfil debts (although this isn’t great for obvious reasons).
Non-flat discount rate term structure
What is the formula for calculating present value?
What discount rate do we use for non-flat discount rate term structures?
Use zero-coupon bond rates (spot rates) of same riskiness as cash flows.
Uncertain cashflows
What is the formula for calculating present value?
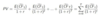
What discount rate do we use for uncertain cash flows?
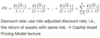
Show the cashflow diagram and the total present value for the whole strategy
Show the cashflow diagram and total present value for strategy B
Formula for rate of return in terms of profit and investment
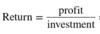
Discounted cash flow formula
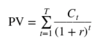
What is the value of $200/year for eternity?
Discount rate = 5%
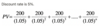
What is the formula for perpetuties?
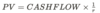
Perpetuities formula proof
Rate of return formula in terms of cash flow and present value
How do we derive the perpetuities formula?
From the rate of return rate formula (r = C/PV), we rearrange so that PV is the subject.
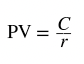
What is an annuity?
A regular payment (it suggests annual payment but it can be any regular payment).
What is the value of $200/year for 5 years?
Discount rate is 5%.
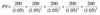
What is the formula for annuities?
Annuity formula explained
Two perpetuities. One starts now (t=0), with the first payment in t=1. The second starts at the end of the annuity, at t=T.
What is the annuity factor?
What is the equivalent annual anuity/cost formula?
Two warnings about the perpetuity formula
- Looks very similar to present value formula but remember PV=CF/(1+r) where as for perputities it is just PV=CF/r
- Regular stream of payments.
How are interest rates usually quoted?
As APRs (rapr) which is associated with k periods.
Formula for EAR
(accounting for compounding frequency k)
Example: One-year investment account. 5% APR, semi annual compounding (k=2). $10,000 investment.
How much money after one-year?
Example: One-year investment account. 5% APR, semi annual compounding (k=2). $10,000 investment.
What is the actual annual rate of interest earnt?
How does compounding frequency impact the Effective Annual Rate?
How do mortgages work in the UK?
Pay 20% down payment
Borrow the rest from the bank using property as collateral
Pay a fixed monthly payment for the life of the mortgage
The option to prepay the mortgage value before the maturity date of the mortgage
Example: house for $500,000 with $100,000 down payment. 30 year fixed rate mortgage at 8.5% APR compounded monthly.
Calculate the monthly payment.
Example: house for $500,000 with $100,000 down payment. 30 year fixed rate mortgage at 8.5% APR compounded monthly.
Calculate the effective annual rate.
Amortisation schedule of mortgages
Same monthly payment, but each month the principal increases and the amount paid to interest decreases, until by the end it is balanced.
How do you calculate the interest and principal paid in mortage payments?
As you have regular monthly payments, once you have calculated the annuity you can calculate interest by multiplying the previous month’s balance by the EAR (APR/12).
Once you have the interest, you can subtract it from the monthly payment to get the principal.
What is NPV?
Net Present Value
the net value of all present values of future cashflows plus the (usually negative) cashflow in period t=0
NPV formulae
Basic rules for NPV
Single project, undertake if and only if NPV > 0
Several independent projects, undertake all with NPV > 0
Mutually exclusive project, take one with highest positive NPV
What does a positive NPV mean? (Even if it just 1 dollar)
r rate represents risk. So a positive NPV means that all risk has been eliminated and all debts have been repaid.
What is IRR?
Internal Rate of Return. The discount rate for which NPV = 0.
How is IRR calculated?
Basic rules for IRR
Independent projects, undertake if IRR > hurdle rate
Mutually exclusive projects, undertake the one with the highest IRR greater than hurdle rate
When do the IRR and NPV methods arrive at the same conclusions?
If and only if:
- Cash flow stream exhibits only one change of sign
- Consideration of only a single project (yes/no decision)
- Hurdle rate is the opportunity cost of capital, also flat
Possible problems with IRR method
More than one change of sign, solving for the IRR might yield multiple solutions.
There may be no solution at all (neither analytical nor numerical).
Multiple mutually exclusive projects → wrong one might be selected.
IRR ignores scale of the project.
Different time patterns of the cash flows.
What do we mean by payback period and discounted payback period?
The minimum length of time s such that the sum of cash flows from a project is positive.
Discounted, when we use present values of cash flows.
Paybath period formula
Discounted payback period formula
Decision rule with payback periods
Accept projects if their payback period is less than or equal to a specified payback period.
Advantages and drawbacks of payback periods
Advantage:
- Simple to communicate
Drawbacks:
- Cutoff period arbitrary
- Rule ignores all cash flows after the cutoff date
- Ignores time-value-of-money effect, equal weight to all cashflows (non-discounted method only)
- It may accept bad short-live projects and reject good long-lived ones.
What is the profitability index?
The ratio of the present value of cash flows and initial investment I0 of a project.
Profitability index formula
PI decision rules
Independent projects: accept all projects with PI > 1 (like NPV)
Mutually exclusive projects: accept the one with the highest PI greater than 1
When do NPV and PI arrive at the same conclusions?
If and only if:
- There is only one cash flow which is at time 0
- Only one project is under consideration
Possible problem with PI
PI scales projects by initial investments. Scaling can lead to wrong answers in comparing mutually exclusive projects.
Of all measurements, which is dominant? Why?
NPV rule dominates - focus on shareholder value maximisation. Others can be misleading:
- IRR ignores the scale of projects
- PI can be an aid when capital is rationed
- Payback rules is the worst
