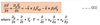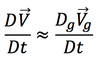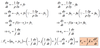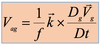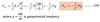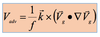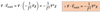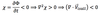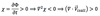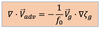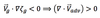chapter 3 Flashcards
The large scale flow in the atmosphere is nearly
geostrophic
the large scale flow in the atmosphere is nearly geostrophic
the ………………. and …………………. are …………………..
wind and mass fields are virtually in balance
the large scale flow in the atmosphere is nearly geostrophic
the wind and mass fields are virtually in balance
In such an atmosphere, the isobars are
straight and parallel and the density is a function of pressure alone (barotropic)
If geostrophy is assumed, there is
no vertical motion and there is no change in the spatial patterns of the height of isobaric surfaces.
If geostrophy is assumed, there is no vertical motion and there is no change in the spatial patterns of the height of isobaric surfaces.
Hence, geostrophy cannot be used to
understand the development of weather systems
Hence, geostrophy cannot be used to understand the development of weather systems, which requires
time changes in the spatial patterns of the height of isobaric surfaces
………………………………………. can be used to understand the development of weather systems in ……………………………….
Quasi-geostrophic theory
a baroclinic atmosphere
In a baroclinic atmosphere, the
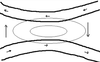
surfaces of constant pressure and density intersect each other forming solenoids that leads to direct circulation and vertical motion.
In a baroclinic atmosphere, the surfaces of constant pressure and density intersect each other forming solenoids that leads to direct circulation and vertical motion.
In such an atmosphere,
the spatial pattern of height field changes with time.
Hence, the slight deviation of geostrophy (quasi-geostrophic) is of great importance to
understanding of atmospheric flow and weather systems
The Quasi-Geostrophic (QG) Momentum Equations
For this analysis, it is convenient to use the
isobaric coordinate system
For this analysis, it is convenient to use the isobaric coordinate system because
- meteorological measurements are generally referred to constant pressure surfaces and
- the dynamical equations are somewhat simpler in isobaric coordinates than in height coordinates.
The scalar and vector horizontal momentum equations in (x,y,z) coordinate system can be written as:

The scalar and vector horizontal momentum equations in (x,y,z) coordinate system can be written as:
where

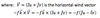
Equation (1) can be transferred to

x,y,p coordinates
Equation (1) can be transferred to (x,y,p) coordinate system as follows:

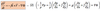
LHS of Eq.(2) can be expanded as follows:
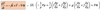
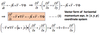
The QG Momentum Equations
Consider the momentum equation in vector form (Eq.3)


The QG Momentum Equations
after considering the momentum equation in vector form
now you should
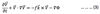
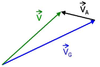
Split the horizontal wind into geostrophic and ageostrophic components
The QG Momentum Equations
after concidering the momentum equation in vector form
plitting the horizontal wind into geostrophic and ageostrophic components:

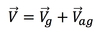
The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
the next step is
Substituting (4) in the coriolis term in (3)
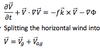
The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
Substituting (4) in the coriolis term in (3):
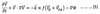
Midlatitude ß-plane approximation
To retain the dynamical effect of the variation of the Coriolis parameter with latitude, f can be approximated by expanding its latitudinal dependence in a Taylor series about a reference latitude O| o

The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
- Substituting (4) in the coriolis term in (3):
The next step is
Now, we replace the Coriolis parameter by f= f0 +ßy , so that the momentum equations (Eq.5) become:
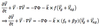
The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
- Substituting (4) in the coriolis term in (3):
- Now, we replace the Coriolis parameter by f = f0 + ßy , so that the momentum equations (Eq.5) become:
the next step is
Expanding the RHS of Eq.(6)

The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
- Substituting (4) in the coriolis term in (3):
- Now, we replace the Coriolis parameter by f = f0 + ßy , so that the momentum equations (Eq.5) become:
- Expanding the RHS of Eq.(6)
the next step is
The last term in (7) is very small, and can be ignored, so we now have:

The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
- Substituting (4) in the coriolis term in (3):
- Now, we replace the Coriolis parameter by f = f0 + ßy , so that the momentum equations (Eq.5) become:
- Expanding the RHS of Eq.(6)
- The last term in (7) is very small, and can be ignored, so we now have
but the next step is
By the definition of the geostrophic wind

The QG Momentum Equations
- Consider the momentum equation in vector form (Eq.3):
- Splitting the horizontal wind into geostrophic and ageostrophic components:
- Substituting (4) in the coriolis term in (3):
- Now, we replace the Coriolis parameter by f = f0 + ßy , so that the momentum equations (Eq.5) become:
- Expanding the RHS of Eq.(6)
- The last term in (7) is very small, and can be ignored, so we now have
- By the definition of the geostrophic wind
the next step is
Substituting (9) in (8), the first two terms on the right-hand side of (8) cancel, resulting in