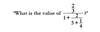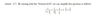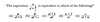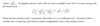Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

Sherpa GMAT 2016 > GMAT 01 - Fractions & Decimals > Flashcards

GMAT 01 - Fractions & Decimals Flashcards

1
Q

3/8 + 1/2 = ?

A

LCD = 8

= 7/8

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

3 + 1/4 = ?

A

3 + 1/4 = 3 1/4

= 13/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

Fractions within the Denominator trick

A

Fractions that contain a fraction in the denominator can be simplified by putting the numerator over one and multiplying the numerator by the “flip” of the denominator

example:

2/(1/3)

= (2/1) / (1/3)

= (2/1) x (3/1)

= 6

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

5/7 - 1/3 = ?

A

LCD = 21

= 8/21

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Simplify the Fraction:

75/300

A

= 1/4

( 75/300 = (3x25) / (3x100) = 25/100 )

( 25/100 = (1x25) / (4x25) = 1/4 )

This fraction breaks down twice

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

How do you convert a fraction into a mixed numeral?

A

1) Divide the numerator by the denominator. The number of times that the denominator can go into the numerator determines the whole number portion of the mixed numeral
2) Place the remainder over the denominator. The resulting fraction is the fractional portion of the mixed numeral.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

5/7 - 2/7 = ?

A

= 3/7

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

(y/4) / (y/x) = ?

A

= x/4

(y/4) / (y/x) = (y/4) x (x/y)

(y’s eliminate)

= (1/4) x (x/1)

= x/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

(2a/3b) / 2ac = ?

A

= 1/3bc

(2a/3b) / 2ac

= (2a/3b) / (2ac/1)

= (2a/3b) x (1/2ac)

= 2a/6abc

= 1/3bc

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

3 3/4 x 7 1/3 = ?

A

= 55/2

3 3/4 x 7 1/3

= (12/4)+(3/4) x (21/3)+(1/3)

= 15/4 x 22/3

(common denominator = 4x3 = 12)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

6 / (4x-x) = ?

A

= 2/x

6 / (4x-x)

= (2)(3) / (3x)

= 2/x

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

X - 1/4 = ?

A

LCD = 4

= (4x-1)/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

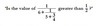
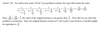
1/5 + 2/5 =

A

= 3/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

(ab2c)/(abc) x (ac)/(abc) = ?

A

= 1

(ab2c)/(abc) x (ac)/(abc)

= b(abc)/(abc) x (ac)/(abc)

= (b)/1 x (ac)/abc)

= abc/abc

= 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

4 - 1/5 = ?

A

LCD = 5

= 19/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
17
Q

14/9 x 6/21 = ?

A

= 4/9

14/9 x 6/21 = (2x7)/(3x3) x (3x2)/(3x7)

7s and one set of 3s cancel

= (2/3) x (2/3)

= 4/9

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
18
Q

6 + 2/x = ?

A

6 + 2/x = 6 2/x = (6x + 2) / x

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
19
Q

Simplify the Fraction:

14/98

A

= 1/7

( 14/98 = (2x7) / (2x49) = 7/49 )

( 7/49 = (1x7) / (7x7) = 1/7 )

This fraction breaks down twice

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
20
Q

7 1/4 - 4 1/2 = ?

A

= 11/4

7 1/4 - 4 1/2

= (28/4)+(1/4) - (8/2)+(1/2)

= 29/4 - 9/2

(common denominator = 4)

29/4 - (2/2)(9/2)

= 29/4 - 18/4

= 11/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
21
Q

Fractions within the Numerator Trick

A

Fractions that contain a fraction in the numerator can be simplified by putting the denominator over one and multiplying the numerator by the “flip” of the denominator

Example:

(2/3)/4

= (2/3) / (4/1)

= (2/3) x (1/4)

= 2/12

= 1/6

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
22
Q

Convert into a Mixed Fraction:

38/7

A

= 5 3/7

( 38/7 = 5 remainder 3)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
23
Q

Convert into a Mixed Fraction:

25/4

A

= 6 1/4

(25/4 = 6 remainder 1)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
24
Q

(11-1) / (2+3) = ?

A

= 2

(11-1) / (2+3)

= 10/5

= 2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
25
Q

How do you add fractions with different denominators?

A

To add fractions with different denominators

1) first you must ffind the lowest common denominator (LCD)
2) then you must convert each fraction to be added into a new fraction by multiplying the numerator and the denominator of each fraction by the value that raises each denominator to the LCD.

This process is known as converting fractions to equivalent fractions

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
26
Q

Simplify the Fraction:

24x4y3/18x2y2

A

= 4x2y/3

( 24x4y3/18x2y2 = {(4x2y)(6x2y2)} / (3)(6x2y2) = 4x2y/3 )

The 6x2y2s cancel out

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
27
Q

If the numerator of a fraction is zero

A

The value of the fraction is zero

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
28
Q

(1+2) / 6 = ?

A

= 1/2

(1+2) / 6

= 3/6

= 1/2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
29
Q

How do you simplify a fraction that contains a fraction within its numerator and/or denominator?

A

To simplify a fraction that contains a fraction within its numerator and/or denominator, always multiply the numerator by the “flip” of the denominator.

example =

(2/5) / (1/3)

= (2/5) x (3/1)

= 6/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
30
Q

How do you subtract whole numbers and fractions from one another?

A

To subtract whole numbers and fractions from one another:

a) place the whole number over 1
b) find the LCD between the whole number and the fraction
c) convert the numbers to a shared denominator
d) subtract one number from the other

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
31
Q

X + 4/5 = ?

A

X + 4/5 = X 4/5 = (5x + 4)/5

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
32
Q

Definition: Reciprocals

A

Reciprocals are any two numbers whose product equals 1.

>> While commonly thought of as “flips” that there are also reciprocals that assume different forms – in particular, look to reciprocals involving roots <<

It is also important to remember that a fraction may have more than one reciprocal

>> To determine whether two numbers are reciprocals, always multiply them together <<

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
33
Q

Simplify the Fraction:

700/28

A

= 25

( 700/28 = (7x100) / (7x4) = 100/4 )

( 100/4 = (25x4) / (4x1) = 25)

This fraction factors twice

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
34
Q

12/(2/5) = ?

A

= 30

12/(2/5)

= (12/1) x (5/2)

= 60/2

= 30

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
35
Q

(Y/4) x (Y/X) = ?

A

= Y2/4X

(Y/4) x (Y/X) = (YxY) x (4X)

= Y2/4X

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
36
Q

Rule: Working with Mixed Numerals

A

When working with mixed numerals, always convert the mixed numerals into fractions before adding, subtracting, multiplying, or dividing.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
37
Q

How to express a whole number as a fraction

A

Set the whole number as a fraction over 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
38
Q

What is the reciprocal of k + (g/x), where k+(g/x) does not = 0?

A

= x/(kx+g)

k + (g/x)

= (k/1)(x/x) + (g/x)

= (kx + g)/x

Reciprocal = x/(kx + g)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
39
Q

5 + 2/3 = ?

A

5 + 2/3 = 5 2/3

= 17/3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
40
Q

(173 + 172) / (172) = ?

A

= 18

<< Complex Numerator Shortcut>>

(173 + 172) / (172​)

= (173/172) + (172/172)

= (17/1) + 1

= 18

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
41
Q

15/100 x 45 = ?

A

= 27/4

15/100 x 45 = (5x3)/(4x5x5) x (3x3x5)/1

= 3/4 x (3x3)

= 27/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
42
Q

(282 + 28) / 28 = ?

A

= 29

<< Complex Numerator Shortcut>>

(282​ + 28) / 28

= (282/28) + (28/28)

= (28/1) + 1

= 29

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
43
Q

In which of the following pairs are the two numbers reciprocals?

a) 2/5 and 5/2
b) (root 5/2) and (2 root 5/5)
c) (root 5/2) and (2/root 5)

A

= a, b, and c

all options = 1

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
44
Q

(2 3/4) / (5 1/2) = ?

A

= 1/2

(2 3/4) / (5 1/2)

= (8/4)+(3/4) / (10/2)+(1/2)

= (11/4) / (11/2)

= (11/4) x (2/11)

(eliminate 11s)

= 2/4

= 1/2

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
45
Q

(4x-x) / (2x+7x) = ?

A

= 1/3

(4x-x) / (2x+7x)

= 3x/9x

= (3/3) (x/3x)

= 1/3

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
46
Q

The Complex Numerator Shortcut

A

In complex fractions, if the numerator of a fraction contains addition or subtraction, that fraction can be split to simplify the arithmetic.

example:

(282 + 28) / 28 = (282/28) + (28/28)

= 28/1 + 1

= 29

This CANNOT be done with a complex denominator!

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
47
Q

(a/b) / (c/d) = ?

A

= (ad)/(bc)

(a/b) / (c/d)

= (a/b) x (d/c)

= (ad)/(bc)

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
48
Q

(5/80) / (2/24) = ?

A

= 3/4

(5/80) / (2/24)

= (5/5)(1/16) / (2/2)(1/12)

= (1/16) / (1/12)

= (1/16) x (12/1)

= 12/16

= (4/4)(3/4)

= 3/4

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
49
Q
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
50
Q

(y-x) / (x) = ?

A

= (y/x) - 1

<< Complex Numerator Shortcut >>

(y-x) / (x)

= (y/x) - (x/x)

= (y/x) - 1

51
Q

How do you multiply fractions?

A

To multiply fractions:

1) multiply the numerators together
2) then multiply the denominators together

To save time, be sure to rip up the numerators and denominators by factoring and canceling out the common terms.

52
Q

1/y + y/3 = ?

A

LCD = 3y

(3 + y2)/3y

53
Q

Simplify the Fraction:

6/8

A

= 3/4

( 6/8 = (2x3) / (2x4) = 3/4 )

(the 2s cancel)

54
Q

Simplify the Fraction:

900/18

A

= 50

( 900/18 = (9x100) / (9x2) = 100/2 )

( 100/2 = (2x50) / (2x1) = 50 )

This fraction factors twice

55
Q

Definition of a Fraction

A

A fraction is a number in the form a/b, where a andb are integers and b does not equal zero

56
Q

(x/y) / (1/5) = ?

A

= 5x/y

(x/y) / (1/5) = (x/y) x (5/1)

= 5x/y

57
Q

x + (y/z) = ?

A

x + (y/z) = x (y/z)

= (xz + y)/z

58
Q

7/x + 5/x = ?

A

= 12/x

59
Q

How do you divide a fraction by a fraction?

A

To divide a fraction by another fraction, flip/invert the second fraction (the divider) and multiply it by the first fraction

ex. (1/4) / (2/5) = (1/4) x (5/2)

= 5/8

60
Q

Definition: Complex Fraction

A

A complex fraction is any fraction that contains addition or subtraction in either the numerator or the denominator.

To simplify complex fractions, you must carry out the addition or subtraction in the numerator and/or denominator before simplifying the resulting fraction

>> Terms can only be cancelled within simple fractions <<

(you cannot factor out from the top and bottom if that factor only applies to one figure within the complex element of the fraction)

61
Q

7-(2/x) = ?

A

LCD = x

= (7x-2)/x

62
Q

How do you add whole numbers and fractions?

A

To add whole numbers and fractions:

1) combine the two numbers into a mixed numeral
2) convert the mixed numeral into a single fraction

63
Q
A
64
Q

Definition: the number on top of a fraction

A

The Numerator

65
Q

(2a/3) / (4b/3) = ?

A

= a/2b

(2a/3) / (4b/3)

= (2a/3) x (3/4b)

= 6a/12b

= a/2b

66
Q
A
67
Q

(a+b)/b = ?

A

= (a/b) + 1

<< Complex Numerator Shortcut>>

(a+b)/b

= (a/b) + (b/b)

= (a/b) + 1

68
Q

Simplify (3 1/2 x 1 1/4) + [(1 5/4) / (2/5)}

A

= 10

(3 1/2 x 1 1/4) + [(1 5/4) / (2/5)}

= {(6/2 + 1/2) x (4/4 + 1/4)} + {(4/4 + 5/4) / (2/5)}

= (7/2)(5/4) + {(9/4)/(2/5)}

= (35/8) + {(9/4) x (5/2)}

= (35/8) + (45/8)

= 80/8

= 10

69
Q

(2/xy) - (x/xy) = ?

A

= (2-x)/xy

70
Q

If the denominator of a fraction is zero

A

the fraction is undefined (has no answer)

71
Q

Convert into a Mixed Fraction:

17/7

A

= 2 3/7

(17/7 = 2 remainder 3)

72
Q

3/7 - 1/9 = ?

A

LCD = 63

= 20/63

73
Q

Simplify the Fraction:

24/64

A

= 3/8

( 24/64 = (3x8) / (8x8) = 3/8 )

(One 8 from each expression cancels)

74
Q

(77/14) / (22/30) = ?

A

= 15/2

<< Always factor first – it saves a lot of time >>

(77/14) / (22/30)

= (7/7)(11/2) / (2/2)(11/15)

= (11/2) / (11/15)

= (11/2) x (15/11)

(11’s eliminate)

= 15/2

75
Q

14/3 x 3/7 = ?

A

= 2

14/3 x 3/7 = (2x7)/3 x (3/7)

3s and 7s cancel

= 2

76
Q

14a/(2/b) = ?

A

= 7ab

14a/(2/b)

= (14a/1) (b/2)

= 14ab/2

= 7ab

77
Q

(y/x) / (y/x) = ?

A

= 1

(y/x) / (y/x) = (y/x) x (x/y)

= YX/XY

(all variables eliminate)

= 1

78
Q

Convert into a Mixed Fraction:

18/5

A

= 3 3/5

( 18/5 = 3 remainder 3)

79
Q

(36/5) / 24 = ?

A

= 3/10

(36/5) / 24

= (36/5) / (24/1)

= (36/5) x (1/24)

= 36/120

= (12/12)(3/10)

= 3/10

80
Q

2/(1/3) = ?

A

= 6

2/(1/3)

= (2/1) / (1/3)

= (2/1) x (3/1)

= 6

81
Q
A
82
Q

Any number express as a fraction can also be understood as

A

the result of dividing the numerator by the denominator (which has a decimal equivalent)

83
Q

How do you add two fractions with a common denominator?

A

Two fractions with a common denominator can be added or subtracted by adding or subtracting the numerators, while leaving the denominators the same

84
Q

Find the reciprocal

(1/5) - x

A

= 5/(1-5x)

= (1/5) - (5/5)(x/1)

= (1/5) = (5x/5)

= (1-5x)/5

reciprocal = 5/(1-5x)

85
Q

x/5 + x/3 = ?

A

LCD = 15

= 8x/15

86
Q

What is the value of (2 1/3 + 1 3/4) / (2 5/6 - 1 1/2) ?

A

= 49/16

(2 1/3 + 1 3/4) / (2 5/6 - 1 1/2)

= (6/3+1/3 + 4/4+3/4) / (12/6+5/6 - 2/2+1/2)

= (7/3 + 7/4) / (17/6 - 3/2)

(common denominators = 3x4 = 12 and 6)

= {(4/4)(7/3) + (3/3)(7/4)} / {(17/6) - (3/3)(3/2)}

= (28/12 + 21/12) / (17/6 - 9/6)

= (49/12) / (8/6)

= (49/12) x (6/8)

= (49x6) / (12x8)

= (49x6) / (2x6x8)

(eliminate 6’s)

= 49/(2x8)

= 49/16

87
Q

(4/9) / (4/5) = ?

A

= 5/9

(4/9) / (4/5)

= (4/9) x (5/4)

= 20/36

= (4x5) / (4x9)

eliminate 4’s

= 5/9

88
Q

1/2 x 3/4 = ?

A

= 3/8

1/2 x 3/4 = (1x3) / (2x4) = 3/8

89
Q

Convert into a Mixed Fraction:

20/3

A

= 6 2/3

(20/3 = 6 remainder 2)

90
Q

(13/68) / (52/17) = ?

A

= 1/16

(13/68) / (52/17)

= (13/68) x (17/52)

= (1/17)(13/4) x (1/13)(17/4)

= (13x1)/(17x4) x (17x1)(13x4)

(eliminate 17’s and 13’s)

= (1/4) x (1/4)

= 1/16

91
Q

How do you simplify a fraction?

A

To simplify any fraction, factor the numerator and denominator and cancel out all common terms.

92
Q

(2/3)/4 = ?

A

= 1/6

(2/3)/4

= (2/3) / (4/1)

= (2/3) x (1/4)

= 2/12

= 1/6

93
Q

How do you convert a mixed numeral into a fraction?

A

1) Multiply the denominator by the whole number and add the numerator
2) Place the sum over the denominator

94
Q

Definition: Levels of Fractions

A

Complex Fractions that contain fractions in either the numerator or the denominator can be thought of as having multiple “levels.”

Each “level” typically consists of two terms that need to be added or subtracted.

>> To simplify such fractions, work one “level” at a time, starting with the bottom “level” and progressing upwards <<

Example:

1/(2 + 1/3)

= 1/(2 1/3)

= (1/1) / (7/3)

= (1/1) x (3/7)

= 3/7

95
Q

Convert into a Mixed Fraction:

40/3

A

= 13 1/3

(40/3 = 33 remainder 1)

96
Q

(1/2) / (4/3) = ?

A

= 3/8

(1/2) / (4/3) = (1/2) x (3/4)

= (1x3) / (2x4)

= 3/8

97
Q

(2/3) / (7/5) = ?

A

= 10/21

(2/3) / (7/5) = (2/3) x (5/7)

= (2x5) / (3x7)

= 10/21

98
Q

What is the value of (3 - 1/3) - (5 - 1/5) ?

A

= -32/15

(3 - 1/3) - (5 - 1/5) = (9/3 - 1/3) - (25/5 - 1/5)

= 8/3 - 24/5 = 40/15 - 72/15

= 32/15

99
Q

Simplify the Fraction:

35/42

A

= 5/6

( 35/42 = (7x5) / (7x6) = 5/6 )

(the 7s cancel)

100
Q

(2/5) / (1/3) = ?

A

= 6/5

(2/5) / (1/3)

= (2/5) x (3/1)

= 6/5

101
Q

b/(b/a) = ?

A

= a

b/(b/a)

= (b/1) (a/b)

= a

102
Q

35 x 42/98 = ?

A

= 15

35 x 42/98 = (5x7)/1 x (2x3x7)/(2x7x7)

7s and 2s cancel

= (5x3)

= 15

103
Q
A
104
Q
A
105
Q

1 + x/3 = ?

A

1 + x/3 = 1 x/3

= (3 +x)/3

106
Q

1/2 + 2/3 = ?

A

LCD = 6

1/2 + 2/3 = 3/6 + 4/6 = 7/6

107
Q
A
108
Q

Simplify the Fraction:

XY2/ X2Y

A

= Y/X

( XY2/ X2Y = (Y(XY)) / (X(XY)) = Y/X)

The XYs cancel

109
Q

5 - 2/3 = ?

A

LCD = 3

= 13/3

110
Q

x/5 x 2/3 = ?

A

= 2x/15

x/5 x 2/3 = (2x) / (3x5)

= 2x/15

111
Q

Definition: the number on the bottom of a fraction

A

The denominator

(eg. the fraction 2/3 has a denominator of 3)

112
Q

1 1/5 + 3 1/3 = ?

A

= 68/15

1 1/5 + 3 1/3

= (5/5)+(1/5) + (9/3)+(1/3)

= 6/5 + 10/3

(common denominator = 5x3 = 15)

(3/3)(6/5) + (5/5)(10/3)

= (18/15) + (50/15)

= (18+50)/15

= 68/15

113
Q

(4/30) / (12/105) = ?

A

= 7/6

(4/30) / (12/105)

= (2/2)(2/15) / (3/3)(4/35)

= (2/15) / (4/35)

= (2/15) x (35/4)

= (2x35) / (15x4)

(divide by 2/2)

= (1x35) / (15x2)

= 35/30

= 5x7)/ (5x6)

= 7/6

114
Q

2/3 x 5/7 = ?

A

= 10/21

2/3 x 5/7 = (2x5) / (3x7)

= 10/21

115
Q

What is the value of (2 + 4/5) - (3 + 4/7) ?

A

= -27/35

(2 + 4/5) - (3 + 4/7) = 14/5 - 25/7

= 98/35 - 125/35

= 27/35

116
Q
A
117
Q

(6/b) / 2 = ?

A

= 3/b

(6/b) / 2

= (6/b) / (2/1)

= (6/b) x (1/2)

= 6/2b

= 3/b

118
Q

Definition: Simple Fraction

A

A simple fraction contains no addition or subtraction in either the numerator or the denominator

>> Terms can only be cancelled within simple fractions<<

(you cannot factor out from the top and bottom if that factor only applies to one figure within the complex element of the fraction)

119
Q

Simplify the Fraction:

7/21

A

= 1/3

( 7/21 = (1x7) / (3x7) = 1/3 )

(the 7s cancel)

120
Q

Definition: Mixed Numeral

A

A Mixed Numeral is the combination of a whole number and a fraction

121
Q

(3x2/2XY) x (21Y/6X) = ?

A

= 21/4

(3x2/2XY) x (21Y/6X) = (3)(x)(x)/(2)(x)(y) x (3)(7)(y)/(2)(3)(x)

= (3x)/(2y) x (7y)/(2x)

= (3x7)/(2x2)

= 21/4

122
Q

(x/5) / (3/2) = ?

A

= 2x/15

(x/5) / (3/2) = (x/5) x (2/3)

= (2x) x (5x3)

= 2x/15

123
Q

Find the reciprocal

y + (1/x) = ?

A

= x/(xy+1)

y + (1/x)

= (y/1) + (1/x)

= (x/x)(y/1) + (1/x)

= (xy/x) + (1/x)

= (xy+1)/x

Reciprocal = x/(xy+1)

Sherpa GMAT 2016 (20 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions