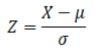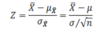Biostatistics (II) Normal & Sampling Distributions

Question 1

What is the most important distribution in all of statistics?

Answer 1

The normal distribution

Question 2

What is the normal (Gaussian) distribution equation?

Answer 2

Question 3

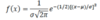
What are the characteristics of a normal distribution?

Answer 3

It is symmetrical around the mean (mu);

mean = median = mode

Question 4

What is the empirical rule of normal distributions?

(i.e. how much of the data falls between 1, 2, and 3 SD?)

Answer 4

1 standard deviation - 68%

2 standard deviations - 95%

3 standard deviations - 99.7%

Question 5

What is the following equation used to calculate?

Answer 5

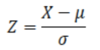
Z = the number of standard deviations above or below the mean that the value (X) lies.

(A Z-transformation of the data)

Question 6

If the mean (mu) is plugged in for the X value in the following equation, what will be the result, and what does it indicate?

(Z-transformation)

Answer 6

The Z value will be 0;

this means that the selected value is exactly in the middle of the normal distribution, no standard deviations higher or lower

Question 7

What equation can be used in a normal distribution to test how different (in standard deviations) a particular value is away from the mean?

Answer 7

Question 8

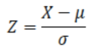
What does a Z value of -1 (using the below equation) indicate about a particular chosen data point?

Answer 8

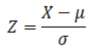
The point (X) is one standard deviation below the mean

Question 9

To what will the average of a group of sample means in a normal distribution be equal?

Answer 9

The population mean (mu)

(i.e. the average of sample means is equal to the population mean)

Question 10

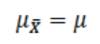
How can the variance of a group of sample means be calculated?

Answer 10

The population variance divided by the square root of the sample size

Question 11

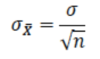
After using the Z score calculated in the equation below to normalize the data, how can we figure out what percentage of the data falls below a particular value (say, a value found at 2 SD above the mean?)?

(e.g. how much of the data falls below the point 2 standard deviations above the mean in a normal distribution?)

Find

(Hint: no extra calculation needed)

Answer 11

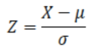
Find the specific Z value on a Z score table.

(in this example, find +2 on the Z score table. The value is 0.9772.

97.72% of the data falls below two standard deviations.)

Question 12

How can we find the probability that a value picked at random from a normal distribution will be between -2.55 and +2.55 standard deviations?

Answer 12

Normalize the data using the Z score;

find the Z scores on the Z score table

(note: the upper value - the lower value will give you the probability of a data point being between those two points)

(for this example, 0.9946 - 0.0054 = 0.9892 (98.9%))

Question 13

How can we find the probability that a value picked at random from a normal distribution will be between greater than or equal to a Z of 2.71?

Answer 13

Find a Z Score of 2.71 on the Z Score table;

1 - table value = answer

(1 - 0.9966 = 0.0034 (0.34% of values above 2.71 SD))

Question 14

What are some of the useful characteristics of creating a sampling distribution from a normally distributed population?

(i.e. taking a sample n of certain characteristics (X-bar, variance, etc.))

Answer 14

The sampling distribution of X-bar is normal.

Mu_x-bar = Mu

σ² = σ / SQRT(n)

Question 15

What are some of the useful characteristics of creating a sampling distribution from a nonnormally distributed population?

(i.e. taking a sample n of certain characteristics (X-bar, variance, etc.))

Answer 15

The sampling distribution is approximately normal

Mux-bar = Mu

σ2 = σ / SQRT(n)

Question 16

What is the Z-transformation equation for a sampling distribution?

(Hint: the equivalent equation for the Z-transformation equation for normal distributions that is listed below)

Answer 16