Brainscape's Knowledge GenomeTM

Browse over 1 million classes created by top students, professors, publishers, and experts.


See full index

12SDD 2023 > 9.2.2 Planning and designing > Flashcards

9.2.2 Planning and designing Flashcards

1
Q

Name the four basic data types

A

Integer, float, string, boolean.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
2
Q

Name the 2 basic data structures

A
  1. Arrays, which could be multidimensional (arrays of arrays).
  2. Records, which is a single data item consisting of a number of named fields.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
3
Q

True or False - in this course, arrays must contain the same data type.

A

True!

In some languages like C and Java when the array is declared so must the data type of all the elements in the array.

However, many real-world languages like Python and JavaScript allow for arrays to be composed of many different data types.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
4
Q

Name and describe the 3 control structures used in algorithms and the various sub-types of each.

A
  1. Sequence - operations in an algorithm are performed in order.
  2. Decision (branching) - different actions are taken depending on a particular condition.
    • Binary decision (IF…ELSE…ENDIF)
    • Multiway decision (CASEWHERE…ENDCASE)
  3. Iteration (looping) - the same series of steps are
    • Pre-test loop (WHILE…ENDWHILE)
    • Post-test loop (DO…WHILE)
    • Counting loop (FOR…NEXT)
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
5
Q

Draw the following algorithm flowchart symbols:

  1. Terminators (BEGIN/END)
  2. Process
  3. Decision
  4. Input/output
  5. Subroutine call
A
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
6
Q

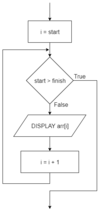
How would the following algorithm snippet be represented with a flowchart?

FOR i = start to finish

    DISPLAY arr(i)

NEXT i
A

Since there is no counting loop in a flowchart, the algorithm would have to be implemented with a pre-test loop.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
7
Q

Write an algorithm to find and return the minimum value of an array called numbers, given that each element in the array could take on any value.

A 
BEGIN minimum
  min = numbers(1)
  FOR i = 2 to length of numbers
    IF numbers(i) < min THEN
      min = numbers(i)
    ENDIF
  NEXT i
  RETURN min
END minimum
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
8
Q

Write an algorithm to find and return the maximum value of an array called numbers, given that each element in the array could take on any value.

A 
BEGIN maximum
  max = numbers(i)
  FOR i = 2 to length of numbers
    IF numbers(i) > max THEN
      max = numbers(i)
    ENDIF
  NEXT i
  RETURN max
END maximum
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
9
Q

Write an algorithm to return the sum of all the elements in an array called numbers.

A 
BEGIN sum
  sum = 0
  FOR i = 1 TO length of numbers
    sum = sum + numbers(i)
  NEXT i
  RETURN sum
END sum
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
10
Q

Write an algorithm to return the average of all the elements in an array called numbers.

A 
BEGIN average
  sum = 0
  FOR i = 1 TO length of numbers
    sum = sum + numbers(i)
  NEXT i
  RETURN sum / length of numbers
END average
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
11
Q

Write an algorithm SimpleFind(item, arr) that searches for a value item in an unsorted array arr and returns True or False, depending on whether the item was found. The algorithm need not terminate once the element has been found the first time.

A

Because the data are unsorted, a linear search must be used.

BEGIN Find(item, arr)
  found = False
  FOR i = 1 TO length of arr
    IF arr(i) = item THEN
      found = True
    END IF
  NEXT i
  RETURN found
END
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
12
Q

Write an algorithm LinearSearch(item, arr) that returns True if item is found in arr or False otherwise. The algorithm should terminate once the item is found and only contain a single RETURN statement.

A 
BEGIN LinearSearch(item, arr)
  found = False
  index = 1
  WHILE index <= length of arr AND found = False
    IF arr(index) = item THEN
      found = True
    END IF
    index = index + 1
  ENDWHILE
  RETURN found
END LinearSearch
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
13
Q

What are the two types of file access and how do they differ?

A
  1. Seqential - data is stored in a continuous stream, and must be accessed from beginning to end.
  2. Random access - Used to store records, an application is able to jump straight to any individual record.
How well did you know this?
1
Not at all
2
3
4
5
Perfectly
14
Q

What is a priming read?

A

In a sequential file, a pre-test loop is used to repeatedly read from the file, which exits when EOF or a sentinel value is found. There needs to be a priming read before this condition is checked so that the algorithm will work if the file is empty.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
15
Q

What is a sentinel value?

A

A sentinel value is a “dummy value” used to indicate the end of data within a file.

Note: While it is more commonly applied to sequential files, a sentinel may also be used when getting an unknown number of inputs from the user. For example, in a CLI application the user might be asked to repeatedly enter data, or a blank value to exit. In this case, the blank value is the sentinel.

How well did you know this?
1
Not at all
2
3
4
5
Perfectly
16
Q

Write an algorithm to open a sequential file and print the contents until EOF is found.

A 
BEGIN
  OPEN somefile for Input
  READ item from somefile
  WHILE NOT EOF
    DISPLAY item
    READ item from somefile
  ENDWHILE
  CLOSE filename
END
17
Q

Write an algorithm to open a sequential file and print the contents until the sentinel value “-1” is found.

A 
BEGIN
  OPEN somefile for Input
  READ item from somefile
  WHILE item != -1
    DISPLAY item
    READ item from somefile
  ENDWHILE
  CLOSE filename
END
18
Q

Write an algorithm printEmployee(empID, file) that prints the employee name with the given empID from the file. Each employee record includes the fields EmployeeID, FName and LName.

A 
BEGIN printEmployee(empID, file)
  OPEN file for relative access
  READ EmployeeData INTO EmployeeID, FName, LName USING empID
  DISPLAY FName, LName
  CLOSE file
END printEmployee
19
Q

Write an algorithm addLog(info) that appends info to the end of a file called ActivityLog.dat

A 
BEGIN addLog(info)
  OPEN ActivityLog.dat for Append
  WRITE info to ActivityLog.dat
  CLOSE ActivityLog.dat
END addLog
20
Q

Explain how binary search works

A

On each pass of the algorithm, the middle value is compared against the search value. Based on the comparison, the list is split into 2, with 1 half discarded and the process repeated with the other half.

Crucially, the data must be sorted for binary search to work.

21
Q

Under what circumstances would linear search be used instead of binary search?

A

Binary search is much quicker than linear search, but the data must be sorted.

So linear search would only be used if the data were unsorted.

22
Q

Compare the cost (number of comparisons) of linear and binary search.

A

For linear search, the maximum number of comparisons is equal to the number of items in the list.

For binary search, the size of the list halves each time. This means that the maximum number of comparisons needed, n, is when 2n is greater than the size of the list.

For example, for a list with 1000 elements:

  • A linear search could take 1000 comparisons.
  • A binary search would at most take 10 comparisons, because 210 = 1024 (note that 29 = 512).
23
Q

Explain how insertion sort works.

A

The list is divided into a sorted part and an unsorted part. For the first item in the unsorted part, find the correct position in the sorted part and insert the item into that position. Repeat until all items are sorted.

24
Q

Explain how selection sort works.

A

The list is divided into a sorted part and an unsorted part. Use a linear search to find the smallest item in the unsorted part and swap with the front of the unsorted part. Repeat until all items are sorted.

25
Q

Explain how bubble sort works

A

Compare adjacent pairs of items, swapping if needed. Repeat until no more swaps are needed.

26
Q

Show how the following array would change with each pass of the selection sort algorithm:

5, 4, 8, 6, 7, 3, 1, 2

A

Original: 5, 4, 8, 6, 7, 3, 1, 2

  1. 1, 4, 8, 6, 7, 3, 5, 2
  2. 1, 2, 8, 6, 7, 3, 5, 4
  3. 1, 2, 3, 6, 7, 8, 5, 4
  4. 1, 2, 3, 4, 7, 8, 5, 6
  5. 1, 2, 3, 4, 5, 8, 7, 6
  6. 1, 2, 3, 4, 5, 6, 7, 8
  7. 1, 2, 3, 4, 5, 6, 7, 8
27
Q

Show how the following array would change with each pass of the insertion sort algorithm:

5, 4, 8, 6, 7, 3, 1, 2

A

Original: 5, 4, 8, 6, 7, 3, 1, 2

  1. 4, 5, 8, 6, 7, 3, 1, 2
  2. 4, 5, 8, 6, 7, 3, 1, 2
  3. 4, 5, 6, 8, 7, 3, 1, 2
  4. 4, 5, 6, 7, 8, 3, 1, 2
  5. 3, ​4, 5, 6, 7, 8, 1, 2
  6. 1, ​3, ​4, 5, 6, 7, 8, 2
  7. 1, 2, ​3, ​4, 5, 6, 7, 8
28
Q

Show how the following array would change with each pass of the bubble sort algorithm:

5, 8, 7, 6, 4

A

Original: 5, 8, 7, 6, 4

  1. 5, 8, 7, 6, 4
  2. 5, 7, 8, 6, 4
  3. 5, 7, 6, 8, 4
  4. 5, 7, 6, 4, 8
  5. 5, 7, 6, 4, 8
  6. 5, 6, 7, 4, 8
  7. 5, 6, 4, 7, 8
  8. 5, 6, 4, 7, 8
  9. 5, 4, 6, 7, 8
  10. 4, 5, 6, 7, 8
29
Q

In a multidimensional array, explain how an algorithm would access each element in array.

A

By using nested FOR loops. For example, to print everything in a 2 dimensional array called 2dArray with “dimensions” 4 by 6 for example:

FOR i = 1 to 4
  FOR j = 1 TO 6
    DISPLAY 2dArray(i, j)
  NEXT j
NEXT i

12SDD 2023 (9 decks)

Brainscape helps you reach your goals faster, through stronger study habits.
© 2024 Bold Learning Solutions. Terms and Conditions