General Math Cards Flashcards
What are the outcomes when Adding and Subtracting Even and Odd numbers?
Even ± Even = Even
Even ± Odd = Odd
Odd ± Odd = Even

Outcomes when Multiplying Odd and Even numbers?

How can you figure out if something is divisible by 3?
If the sum of the digits in a number add up to a value that is divisible by 3, then the number itself is divisible by 3.
What is a trick to figure out if a number is divisible by 4?
That the last two digits of a number, and if this value is divisible by 4 then you know the whole number itself is divisible by 4.
How do you know if a number is divisible by 5?
Just needs to have a 5 or 0 at the end…
How do you figure out if a numebr is divisible by 6?
If a number is divisible by 2 (even) and 3 (the sum of all digits is divisible by 3) then you know that the number is divisible by 6.
How do you figure out if a number is divisible by 8?
If the last three digits form a number that is divisible by 8.
How do you figure out if a number is divisible by 9?
If the sum of the digits is divisible by 9 then the number itself is divisible by 9.
729 / 9
(7+2+9) / 9
18/9
Which is 2 so 729 is divisible by 9.
How do you figure out if a number is divisible by 11?
If, when writing the signs -+-+ alternatively between the digits, the sum result is value divisible by 11.

What are all the prime factors up to 50?
2, 3, 5, 7, 11, 13, 17, 23, 29, 31, 37, 41, 43, 47
Two is the smallest prime number and its the only that’s even, the rest are odd.
What is something to remeber about the odd even relationship of prime numbers?
Two is the smallest prime number and its the only that’s even, all the rest are odd.
If they were even they would be divisible by 2.
Is 1 a prime number?
It isn’t because it cannot be divided by two different factors.
Are 51 and 91 prime numbers?
No.
51 is 3 * 17
and
91 is 7 * 13
Prime Numbers: An integer can only be divided by?
1
itself
its prime factors
and integers created by multiplying some of its prime factors with other prime factors.
When figuring out if a number is divisible by a set of numbers given, what do you need to remember?
That you can use the prime numbers to multiply into different multiples as many times as they appear when factoring down.
For example, if there are three 2s from factoring 120 down you can use 2 three times to create new factors.
What technique can we use to figure out whether a number is prime?
Technique: if a number is not divisible by any prime number smaller than its root then its a prime number. If it is divisible, it is not prime.
Once you know the root, and figured out out all the prime numbers below it, divide the original number (i.e. before the root) by the primes and if they don’t divide the number itself is prime.
How do we calculate the root of a number without a calculator? For example, the square root of 71.
By memorizing the mutliplication table we can estimate the root between the common values we do know.
With 71 we know that 8*8 is 64 and 9*9 is 81, so we know the root of 71 lies in between 8 and 9.
What is the best technique to find the GCF between two numbers?
- List out all the prime factors of both numbers
- What prime factors are in common? In what number do the appear least? Get all prime factors and list the prime number in the quantity where it appears least.
- Now multiply the prime factors by eachother to get the GCF.
The Greatest Common Factor is the largest factor that divides evenly into all numbers in a set.
What is the fact technique to find the Least Common Multiple (LCM) between two numbers?
For example for 33 and 36
- List out all the prime factors of both numbers
- Add all the prime factors to one list but importantly list the common prime factors in the quantity where they appear most, do not add them double. Any prime factors that are not common are just listed as is.
- Now multiple all the factors together to get the LCM
The prime factors of 33 are 3,11 and the prime factors of 36 are 2,2,3,3. The resulting list is 2,2,3,3,11. Multiplying this out gives: 396
Data Sufficiency: General Answer Choices Structure
- A - picking statement A
- B - picking statment B
- C - Combined, combining information would be enough to answer the question.
- D - Divided / or, each one on their own is enough to answer the question.
- E - E…impossible, even both combined together not enough information.
What is the purpose of Data Suffiency questions?
The purpose is of data suffiency questions is not to solve the question but rather you have to figure out if the question can be solved.
You DO NOT have to answer the question, just whether or not you can come up with a answer.
Can you trust sizes and proportions (such as apparent right angles) if theyre not explicility stated?
No, you can’t trust what you see.
An angle can be much larger or smaller than what it looks. Same goes for lines, areas or any other measurement.
Is zero divisible any number?
Zero is divisible by any number, except itself.
What is an acute angle? What is an obtuse angle? What is a reflex angle?
Acute = angle less than 90º
Obtuse = angle greater than 90º
Reflex Angle= angle larger than 180º but less than 360º
What is a bisector?
A bisector is a line, line segment or ray that passes through the middle of a line segment or through the middle of an angle, and divides them into two equal parts.
What is a neat way of remembering how the angles relate when parallel lines are crossed by another line?
F U N
Where the angles in F and N are equal, large and small angles, while you can imagine angles in more squared U to be different but the sum of them both is 180º.
Geometry: can straight lines be trusted when doing angle calculations?
Yes they can, but always double check.
What is something you should really do when you first see a question?
Read it carefully, make sure you don’t glaze over any important words and make sure you truly understand what they are asking.
Is 0 rational?
Yes, because it can be written as a fraction. For example, 0/7.
What are proper and improper fractions?
Proper fractions are fractions where the numerator is smaller than the denominator.
Improper fractions are frations where the numerator is greater than the denominator. Improper frations can be equal to integers, i.e. the numerator can be divided without remainder by the denominator.
What is a better way of adding fractions when both denominators produce a large number when multiplied?
You find the Least Common Multiple of both numbers. You do this by finding all prime factors, adding them to one list where the quantity of a factor is determined by where it occurs most, and finally taking the product of this list.
Once found, you multiply the fractions, numerator and denominator, by the neccessary values to get them to the LCM.
What are the decimals and percents of 1/8 and 1/6
1/8: 0.125 12 1/2 %
1/6: 0.1666… 16 2/3 %
What’s an important condition for this relation?
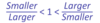
The values need to be positive.
-ve vlaues would satisfy the greater than signs, but not be following the larger and smaller relation.
Buying and Selling Products: What is the Cost price and what is the Expense?
What is the selling price and revenue?
Cost price is the basic price demanded by the person who produced the good.
The total cost of all the items bought by a seller is called the expenses.
The selling price is the price for which the goods are sold to the customers.
Revenue is the total sum recieved from selling items to customers.
What is simple interest?
Simple interest doesn’t take into account compounding and thus every year you receive or pay the same amount determined by the principal amount.
With Data Sufficiency questions, what approach should you take?
You need to take the Logical approach
What are the variables we need to know to solve simple interest problems?
How many of those variables are needed in simple interest data sufficiency questions?
In simple interest questions we need to know 3 of the following 4: interest, principal, rate or time periods.
With data sufficiency problems, knowing 3 of the 4 means there is enough data to answer the question at hand.
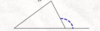
What is the external angle of a triangle equal to?
An external angle to a triangle is equal to the sum of the other two internal angles, the ones that it is not adjacent to.









