C4: Nominal n Effective Interest

Question 1

Nominal interest rate

Answer 1

• r* = Nominal interest rate
• *does not include the impact of compounding**

i = interest rate per
compounding period

m = num. of compounding
periods per year

r = i·m

Question 2

Effective interest rate per year

Answer 2

Question 3

i

Answer 3

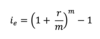
i = interest rate per compounding period

r = nominal interest rate

m = number of compounding periods per year

Question 4

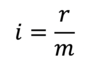
If the interest rate is compounded continuously, then the effective continuous interest rate is as follows:

Answer 4

Note: i and r are expressed in terms of 1 year

Question 5

Example One:

If the nominal interest rate is 6% per year, compounded monthly…

What is the interest rate per month?

Answer 5

r = 6% per year
compounded monthly.

m = 12 months / year.

i = r / m
= 6% / 12
= 0.5% per month.

Question 6

Example Two:

If the nominal interest rate is 6% per year, compounded monthly…

What is the effective interest rate per year?

Answer 6

r = 6% per year
compounded monthly.

m = 12 months per year.

ie = (1 + r/m)^m - 1

ie =(1 + 0.06/12)^12 – 1

ie = (1.005)^12 - 1

ie = (1.0616778) - 1

ie = 0.0617 = 6.17%

Question 7

Example Three:

If the nominal interest rate is 6% per year, compounded continuously, what is the effective continuous interest rate per year?

Answer 7

r = 6% per year compounded continuously.

e = 2.71828

i = e^r - 1

i = 2.71828^0.06 - 1

i = 0.0618 = 6.18%

Question 8

Example Four:

The nominal interest rate is 6% per year, compounded quarterly. If $2,000 is deposited now, then how much will it be worth in six years?

Answer 8

r = 6% per year
compounded quarterly.

m = 4 quarters per year.

i = r / m = 6%/ 4
= 1.5% per quarter.

n = 4 qrters/yr · 6 yrs
= 24 quarters
= 24 compounding periods

P = $2,000

F = ?
F = $2,000 (F/P, 1.5%, 24)
F = $2,000 (1.4295)
**F = $2,859.00**

Question 9

Example Five:
The nominal interest rate is 6% per year, compounded semiannually. If $3,000 is deposited at the end of each six-month period for five years, then what is the present worth of all of these deposits now?

Answer 9

r = 6% per year compounded semiannually.

m = 2 compounding periods per year.

i = r / m = 6% / 2 = 3% per semiannual compounding period.

n = 2 semiannual periods per year x 5 years = 10 semiannual compounding periods.

A = $3,000 every six months.

P = ?
P = $3,000 (P/A, 3%, 10)
P = $3,000 (8.5302)
**P = $25,590.60**