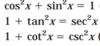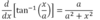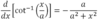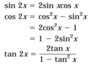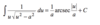Calculus Barrons Flashcards
(162 cards)
1
Q
A derivative of the corner point at point c
A
1
Q
What is the Mean Value theorem?
A
If the function is continuous between [a,b]. Then there must be some point (lets call this point x), where x’s derivative is equal to the average slope of a line connection points (a, y) and (b, y). This information is useful if you those problems that relate to getting a ticket for speeding. If you are travelling down a road and at point A, the police measure your speed to be 60 and then at point B, the police measure your speed to be 65, the time that it took you to travel from point A to point B (5 miles) is .25 hours. Then they can guarantee that at one point along your path from point A to B, you were going (5)/.25 mph at some point. In order to find out whether the Mean Value Theorem is satisfied check whether the function is continuous and then derive the function and check whether the are any values of [a, b] that make the derivative divided by 0 or any other discontinuity
2
Q
In order for there to be a derivative at point C, then
A
- The function must be continuous at that point. Therefore no skips, jumps, holes.
3
Q
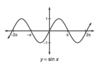
What type of symetry does this function have?
A
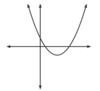
Wrong bitch. The function is shifted 2 spaces to the right, therefore f(x) no longer equals f(-x).
3
Q
Derivative of sec-1x
A
3
Q
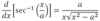
What is “find the line normal to the curve a point P” asking?
A
The normal line means the line that is perpendicular to the tangent at point P. Find the f’(x1) and before plugging it into the point slope form, plug in the inverse so 1/f’(x1).
4
Q
Derivative of efunction
A
efunction times derivative of the function
5
Q
What are considered critical values for the 1st derivative
A
when the 1st derivative = 0 or where the 1st derivative does not exist. also end points
6
Q
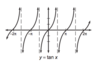
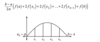
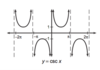
Graph Cscx
A
7
Q
Origin Symetry means the function is
A
The function is odd. f(-x) = -f(x)
7
Q
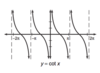
Cot-1(x) in terms of tan
A
Cot-1(x) = pi/2 -tan-1(x)
7
Q
Derivative of csc-1x
A
8
Q
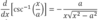
What geometric test must one to one functions pass
A
Horizontal Test
10
Q
The formula that defines a derivative
A
12
Q
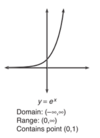
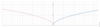
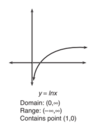
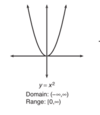
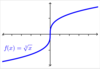
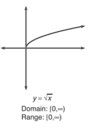
Graph rad(x). Domain and Range?
A
13
Q
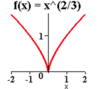
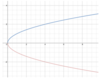
What does -x2 look like in comparison to x2
A
14
Q
List the power reducing formulas
A
14
Q
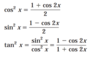
Chapter 3, practice question 50.
lim x2 times sin(1/x)
as x approaches infinity
A
You can not just do sin(1/
15
Q
What is this question asking? “Does limit as x approaches 1 exist in f(x)?”
A
The question is asking if from the left and right side of the function approach the same value. This same value does not have to be defined.
16
Q
Derivative of Cotx
A
-csc2x
17
Q
A function is one-to-one
A
If the function has 1 unique y value for each x value. Therefore in x2 f(-1) and f(1) producing the same y value of 1 would not be considered uniqe, x2 is not 1 to 1
17
Q
Derivative of cos-1x
A
18
Q
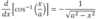
Classift Sinx, Cosx, and Tanx as either odd or even
A
Sinx - odd
Cosx - even
Tanx - odd
18
Q
List the sum and difference formulas
A
18
Formula for factoring cubics
18
Quotient Rule
[(2nd function times derivative of the 1st function) - (1st function times the derivative of the 2nd function)] / (2nd)2
18
How does the derivative of a function relation to the derivative of the function's inverse? What formula?
The derivative of an inverse function is the reciprocal of the derivative of the function, since the derivative of an inverse function is represented by dx/dy not dy/dx.
(f-1)' (x) = 1/ f'(f-1(x))
20
Graph Sinx
21
Which formula would you use to solve a problem like this "If f(x) = 5x and 51.002 = 5.016, which is closest to f'(1)
The formula for a derivative. h = 0.002
22
Exponential Functions
a^0 = 1
a^1 = a
a^m \* a^n = a^m+n
a^m / a^n = a^m-n
24
List all 3 pythagorean identities
26
Graph ex. Domain and Range?
27
Derivative of sin-1x
28
Derivative of tan-1x
29
What does the "+ 4" do to the function (x + 1)2 **+ 4**
The function is shifted up 4 spaces.
30
A function is a function if ...
Every x value has a single y value. Therefore f(-1) can not equal 1 and 2, but f(-1) and f(1) can equal the same y value, since each x value still has a single y value.
31
Graph tanx
32
Graph cotx
33
What does rad(-x) compared to rad(x)?
34
Graph [[X]]. Domain and Range?
36
Graph ln(x). Domain and Range?
37
Derivative of cot-1x
38
Equals
f(g(x))
39
Graph secx
39
Product Rule
(First function times the derivative of the second function) + (the second function times the derivative of the first function)
40
Graph |x|. Domain and Range?
42
How would you represent Sec-1(x) in terms of cosine
Cos-1(1/x). Not 1/**Cos-1(x)**
43
Graph X2 and what is its domain and range.
44
Graph X3. Domain and Range?
46
Derivative of Cosx
-sinx
47
Implicit differentiation occurs when? What do you do in order to solve derivatives that require implicit differentiation?
Implicit differentiation occurs when a function is defined with both x and y as part of the function (e.g. x2 + cos(y)) instead of just y = x2. In order to solve differentiation you have to derivat the x normally and tag on a dy/dx every time you derive the y. Then solve for the dy/dx. If you are asked for the second derivative and given the function. First find the first derivative. Then substitute the value you got for dy/dx from the first derivative into the second derivative. You can have y in your answer for an implicity derived function.
48
A derivative of a cusp at point c
49
Define Rolle's Theorem
Rolle's Theorem is a special case of the the mean value theorem. The roles theorem claims that if a function is continuous between [a,b] and f(a) = f(b), then at some point (lets call this point x) f'(x) = 0, since the graph has to change direct (slope change from positive to negative or negative to positive) in order to return to (b, f(b)).
51
What geometric test must functions pass?
Vertical Line Test
52
List the double angle formulas
53
Synthetic Division
55
Graph Cosx
56
Point-slope formula of slope
y - y1 = f'(x1)(x - x1)
57
lnaxm is equivalent to
m x lnax
59
Simplify ln (3 \* 5)
ln(3) + ln(5)
60
Derivative of constantfunction (e.g. 5x^3)
constantfunction times ln(constant) times derivative of function. 5x^3 times ln(5) times 3x2
61
A derivative of a vertical tangent at point c
Does not exist
63
Derivative of tanx
sec2x = (sec(x))2
64
Graph 1/x. Domain and Range?
65
Where is the tangent to the curve 4x2 + 9y2 = 36 vertical?
1. The tangent line is found by the derivative, so this problem involves deriving in some way
2. So go ahead and derive the function (you will need to use implicit differentiation)
3. Once you have a value for dy/dx, you can move on to finding when the tangent line is vertical.
4. A vertical line is given by f(y) = some constant, because regardless of the y value you plug in, the x value will always be 0.
5. Therefore take the inverse of the dy/dx, which is dx/dy, by finding the reciprocal of dy/dx.
6. Find when dx/dy = 0, then set this y value equal to 4x2 + 9y2 - 36
66
Y semetric means that the function is
The function is an even function. Therefore f(x) = f(-x)
67
In bracket notation, parenthesis represent which type of bounds and brackets represent which type of bond
Parenthesis represent exclusive bounds. So you would use parenthesis when you have negative or positive infinity in the bound, since negative or positive infinity can never be inclusive. Brackets are used for inclusive, therefore [3,10] means that 3 and 10 are included in the range.
68
In order to find the inverse of a function. The function must be
One to one. Think about it, a function is only a function if a x value yields only one y value. So if you were finding an inverse function (meaning you plug in y's and x's come out), you would need the function to be one to one, so that when you have your inverse function and plug in a y value, you do not get more than one x value.
69
Draw the unit circle
70
If a question asks you to write a limit if it exists, it is okay to write infinity or negative infinity. It is implicity understood that this limit does not exist
71
72
Do not worry about the piecewise function taht produces a skip. The limit still exists
73
You can not just cancel the x values. Usually when dealing with absolute value it is better to make a value table and then sketch out the graph. The answer is that the limit does not exist
74
Where is this function discontinuous? What type of discontinuity is it? Can this discontinuity be removed?
Do not ignore the radical, this simplifies to |x-5|/(x-5). Jump @ x = 5, not removable
75
Extreme Value Theorem
Guarantees that there is a maximum and a minumum if the interval closed aka brackets nigga. Also the function has to be continuous. Okay the brackets part makes sense because if the interval was open aka parenthesis, the end point of the interval (which are commonly the maximum and minimum) do not count therefore, there is no guarantee that a maximum or minumum exist. These max and min can still exist on an open interval, but the extreme value theorem can not guarantee the existence of of a max or min. Now just because an open interval exists doesnt mean that the max and min values can be passed onto the values right before these open intervals (e.g. if the open interval is (1, 5) then 1.00001 and 4.9999 can not become the max and min, since the max and min need to plateu off unless the function stops at a closed interval. Obviously the second part of the extreme value theorem makes sense, the function has to absolutely be continuous.
on the closed interval -pi, -pi/4. Then -pi is the max and -pi/4 is the min
76
Rules for finding limit as function approaches - to + infinity
HA are the behavior of the function as x approaches + or - infinity, and therefore HA's can also be found using these rules
77
Special limit with sin
This limit only applies if x approaches 0. If x were approaching infinity, we know that the limit will be zero because sin (infinity) can only produce -1 and 1, and -1 and 1 divided by infinity = 0. This limit of 0 can also be proved by the squeeze theorem.
78
Special limit of cos
79
80
Limit as x approaches infinity of constant/x
81
Tricky problem:
Can not simplify the rad(4x2) to 2x. Instead you have to use the conjugate method to solve.
82
83
84
85
Derivative of cot and csc
86
log derivatives
ax = ax times ln(a)
87
You can approximate a derivative ata certain point by doing what?
Finding the slope of the secant line between (c-1) and c. C are x axis's
88
Finding the derivative of the inverse function without finding the inverse function
Remeber P.I. prime(inverse)
89
90
Cone volume
91
92
93
Step for related rate problems
94
If for a related rate an object is falling or dripping then the object is said to have what type of rate
negative
95
96
Can corner point be relative extrema
Yes corner points can be relative extrema even though corner points can not be derived
97
Explain how to find the area under a curve using the trapezoidal rule
In order to find the width of the trapezoids, it is (b-a)/n. That is it, just like for the midpoint, left & right rieman sums. The (b-a)/2n is in the formula below is different, the 2 in front of the n is averaging the lengths of the trapezoid.
98
Area of a trapezoid
99
100
Tricky maximum problem
101
Distance between two points foruma
This formula comes in handy for first derivative max problems
102
103
104
Position function
g = 9.8
105
106
107
Surface area of a cube
108
109
Volume of cone
110
Volume of sphere
111
112
Area under a curve
113
When should you tag on a
"+ C"
Only when the integral does not have set bounds. So when the elongated s that represents an integral does not have numbers following it. So only tag on "+ C" for indefinite integrals
114
115
When calculating definite integral, what is the sign of the area under the x axis
negative. the area is always signed when calculating definite integrals.
116
Midpoint underestimates
Concave up
117
Midpoint overestimates
concave down
118
Trapezoids underestimate
concave up
119
Trapezoids overestimate
concave down
120
When dealing with + C any operations done to + C or any expression containing + C do not apply to + C. So if I had -(e + C). Then -e + C is the result, since the negative does not effect the + C
121
122
The average value of a function
123
How to plug derivative into fnInt function
124
125
126
127
128
129
130
5 techniques to solving hard integrals
131
5 techniques to solving hard integrals
132
5 techniques to solving hard integrals
133
5 techniques to solving hard integrals
134
5 techniques to solving hard integrals
135
tough motherfucking question
136
137
138
Algo for u-substitution
139
When using u substitution with a definite integral what much occur
140
integral of sec
141
integral of csc
142
integral of cot
143
integral of tanx
144
145
what derives to tan inverse
146
integral of arc sin
147
what is the integral of arc sec
148
149
disk method formula
150
Washer method formula
151
what is special about this example
It requires the disk and washer method in order to solve. Since the segment raises off the x axis and thus has a hole for part of it
152
cross section algo
153
Cross sectional formula of a equilateral triangle
154
range for sin, tan, and csc
155
range for cos, sec, cot
156
formula for exponential growth or exponential decay
y = N times ekt
157
tip
158
159
160
Do functions always have a maximum and minimum
Yes. All function have both a maximum and minimum
161
Speed is always
positive. always include absolute value
162
an object increases speed if
Velocity and acceleration are the same side
