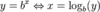Ch 7

Question 1

Exponential Functional Form

Answer 1

Y=ab to the power of x

Question 2

b in Exponential Functional Form

Answer 2

Growth or decay

Question 3

a in Exponential Functional Form

Answer 3

Y intercept at (0,a)

Question 4

Y intercept in Exponential Functional Form

Answer 4

at (0,a)

Question 5

in Exponential Functional Form if b>1

Answer 5

growth

Question 6

in Exponential Functional Form if 0< b<1

Answer 6

decay

Question 7

the sign of the value of a determines the direction of the graph,if a>0

Answer 7

goes upward

Question 8

the sign of the value of a determines the direction of the graph, if a<0

Answer 8

goes downward

Question 9

in modelling exponential functions, growth formula

Answer 9

y=a(1+r)to the power of x

Question 10

in modelling exponential functions, decay formula

Answer 10

y=a(1-r) to the power of x

Question 11

in modelling exponential functions, a

Answer 11

initial amount before measuring growth/decay

Question 12

in modelling exponential functions, r

Answer 12

growth/decay rate (often a percent)

Question 13

in modelling exponential functions , x

Answer 13

number of time intervals that have passed

Question 14

in modelling exponential functions, y

Answer 14

the final amount after measuring growth/decay

Question 15

exponential growth+examples

Answer 15

this means that an initial amount increases at a steady rate over time examples: -population increases -growth of monetary investments

Question 16

exponential decay+examples

Answer 16

this means that the initial amount decreases at a steady rate over a period of time

Question 17

compound interest

Answer 17

when the bank pays interest on the principal and the interest already earned

Question 18

compound interest formula

Answer 18

Question 19

compound interest fomrula for annual

Answer 19

A = P(1 + r)t

Question 20

compound interest formula values

Answer 20

P=principal amount invested

A=the new balance

t=the time in years

r=the rate (in decimal formal)

n=the number of times it is compounded

Question 21

compunded interest values for n

Answer 21

yearly= n=1

Quarterly= n=4

monthly- n=12

daily- n=365

Question 22

logarithmic function

Answer 22

x+log b(small)y

Question 23

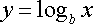
exponential function

Answer 23

y=b to the power of x

Question 24

normal base in logarithmic functions (think calculator)

Answer 24

10

Question 25

the inverse of an exponential function

Answer 25

is a logarithmic function

Question 26

rule for converting exponential functions to logarithmic functions

Answer 26

Question 27

change of base formula

Answer 27

note change x for y

Question 28

product property

Answer 28

logb(small)(mn) = logb(small)m + logb(small)n

Question 29

Quotient Property

Answer 29

logb(small)(m/n) = logb(small)m - logb(small)n

Question 30

Power Property

Answer 30

logb(small)(m to the power of n) = n logb(small)m.

Question 31

steps for simplifying

Answer 31

- start with the power property - work across with product and quotient property

Question 32

steps for expanding

Answer 32

1. power property if exponents 2. Quotient Property 3. Product Property 4. Power property again if necessary 5. evaluate any logs that are only numbers if they are whole numbers or fractions

Question 33

y=e to the power of x conversion

Answer 33

lny=x

Question 34

base=e=

Answer 34

2.718

Question 35

natural base

Answer 35

ln=logeto the power of x

Question 36

natural vs common

Answer 36

both lografic natural base is common base is 10

Question 37

pert formula

Answer 37

``` P = principal amount (initial investment) r = annual interest rate (as a decimal) t = number of years A = amount after time t ``` A(t)=Pe to rt

Question 38

Rate=

Answer 38

difference/intial value