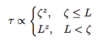Chapter 11: Observables in Phase Transition Flashcards
(8 cards)
1
Q
First-Order Phase Transition
A
discontinuity in the order parameter
2
Q
Second-Order Phase Transition
A
- critical singularity can be described by critical exponent with respect to t = |1 - T/TC|
-
universality class: important here; relevant parameters
- spatial dimensionality D
- symmetry of order parameter
-
universality class: important here; relevant parameters
3
Q
Specific Heat, Magnetization, and Magnetic Susceptibility
A
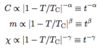
4
Q
Correlation Function
A
- correlation length diverges as T → TC
- details of lattice and short-range behavior become irrelavant → reason for universality
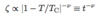
5
Q
Scaling and Hyperscaling
A
- there exist only 2 independent critical exponents
- there exist scaling relationships between critical exponents
6
Q
Finite-Size Scaling Theory
(Overview)
A
- L finite → Z is infinitely differentiable analytic power series → no singularities possible
- maxima are rounded and displaced
- max{ζ} ~= L
7
Q
Finite-Size Scaling Theory
(Assumptions)
A
- consider susceptibility (below)
- actually measure scaling function in simulation
- should get same results regardless of choice of L
- allows for extrapolation of γ/ν, 1/ν, Tc

8
Q
Critical Slowing-Down
A
- correlation time τ for loval MC algorithm given below
- Recall: Neff = N/(2τ)
- as L increases, τ increases faster, meaning much longer time is needed to each the same level of accuracy
- can overcome by using clust algorithms (e.g. Wolff algorithm)