Chapter 6: The Free Electron Gas Flashcards
Specific Heat in Metals: Experimental Results
Typically plot C/T vs T2
Fermi Energy
(3 points)
- From Pauli Principle, each energy level can only contain two electrons. The energy level of the highest filled state is the Fermi level
- Corresponds to a sphere in k-space
- Radius kF = (3π2n)1/3
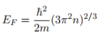
Chemical Potential
(5 points)
- Unlike phonons, number of electrons N is constant
- Leads to chemical potential included in statistics
- Temperature dependence very small
- µ(300K) ≈ EF
- When two objects brought into contact µa = µb
Free Electron Gas: Ground State
(Take-Away: 2 points)
- Energy E = (h-bar)2k2/(2m)
- Well-defined momentum p = (h-bar)k
Drude vs Sommerfeld
(4 points)
-
Drude assumed free mean path l = vthτ
- Scattering at ions → WRONG!
-
Sommerfeld assumed free mean path l = vFτ
- Scattering at imprefections
Free Electron Gas: Boundary Conditions
(Take-Away: 2 points)
- kd = 2πni/Ld for d = x, y, z and i = 0, ±1, ±2, …
- For every k, there exists two electrons (because of spin) with energy
Hall Effect
(Setup: 4 points)
- Smaple has E-field in +x-direction and B-field in the +z-direction
- Current in +x-direction leads to E-field in +y-direction → Hall Field
- Lorentz force in -y-direction until compensated by E-field
- Leads to charge separation
Temperature Dependence of Electrical Conductivity
(2 points)
-
σ = 1/ρ so helpful to understand dependence on resistivity
- Due to scattering of at phonons and defects
Specific Heat - Electronic Contribution: Sommerfeld Approximation
(Assumptions: 2 points)
- Actual internal energy U not solvable analytically
- F(E) only deviated from F(E(T=0)) in region ±kBT around E ≈ µ
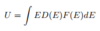
Temperature Dependence of Resistivity
(Graph)
Free Electron Gas
(Assumptions: 3 points)
- Electrons in metal are delocalized
- No electron-ion interactions
- No electron-electron interactions
Hall Effect
(Take-Away)
- Can obtain sign and charge of carriers feom Measure Hall coefficient R = -1/(ne)
Free Electron Gas: Ground State
(Assumptions: 4 points)
- N free electrons
- Volume V = L3
- Temperature T = 0
- Becuase no electron-electron interactions, can solve problem of single electron in a box with volume V
Sommerfeld Model
(Take-Away: 4 points)
- Again σ = neµ
- But, µ = eτ /m with l = vFτ
- Results in higher conductivity
- Fermi velocity used, because only electrons near Fermi energy can participate
2D Electron Gas
(Assumptions: 2 points)
- Potential walls at z = ±L/2
- kz restricted to πn/L for n = 1, 2, 3, …
Temperature Dependence of Resistivity: Phonon Scattering
(6 points)
- High temperature T >> ΘD
- ρ ∝ <n> ∝ T</n>
- Low temperature T << ΘD
- ρ ∝ <n> ∝ T3</n>
- Experiment shows ρ ∝ T<span>5</span>
- Additional T2 comes from scattering angle being small
Low-Dimension Electronic Systems
Obtained by placing potential walls in one or more directions
Temperature Dependence of Thermal Conductivity in Metals
- From Wiedemann-Franz Law: K(T) = LσT ∝ T /ρ
Fermi Gas: Pressure
Electron Density of States in Momentum Space
(2 points)
- One state per unit volume
- Two electrons per state
Drude Model
(Take-Away)
- σ = neµ
Fermi-Dirac Distribution
(3 points)
- Gives the probability that a state with energy E is occupied for a given temperature
- µ ≡ chemical potential
- Because kBT << EF , only small number of electrons redistributed
Fermi Gas: Total Energy per Electron
- Even at T = 0, still very high
Drude Model
(Assumptions: 6 points)
- Electrons in metal behave clasically like a gas of particles
- Move with thermal velocity vth
- Collide with atomic cores
- Acceleration comes from electric field
- Deceleration comes from collision
- Relaxes velocity within τ
Wiedemann-Franz Law
(2 points)
- Gives relationship between thermal conductivity K and electrical conductivity σ
- K/(σT) = L → constant: Lorentz number
Specific Heat - Electronic Contribution: Classical Treatment
(Take-Away)
100x larger than experiment, because of Pauli Principle
Specific Heat - Electronic Contribution: Classical Treatment
(Assumptions: 2 points)
- Each electrons has 3/2*kBT energy
- Factor of 2 from spin
Electron Density of States in Energy Space
(Graphs)
Electron Density of States in Energy Space
(Equations)
Thermal Conductivity in Metals
- Can be calculated according to kinetic gas theory like phonons
- Kph << Kel for metals
Fermi Gas: Compressibility
Temperature Dependence of Electric Conductivity
(Graph)
Specific Heat - Electronic Contribution: Sommerfeld Approximation
(Take-Away: 3 points)
- Only electrons near EF can redistribute and contribute to specific heat
- Number of electrons Nth ≈ D(EF)kBT
- Justification for CV ∝ T
Electrical Conductivity
Electron Motion in Magnetic Field
- Electrons now feel Lorentz force
