Chapter P Flashcards
Multiplying Conjugates
Difference of Two Squares
variable
a letter used to represent various Numbers
Special Products
Simplifying Exponential Expressions
Finding the Least Common Denominator
Adding and Subtracting Rational Expressions That Have Different Denominators
Factoring the Sum or Difference of Two Cubes
Finding nth Roots of Perfect nth Powers
Associative Property of Addition
Changing grouping when adding does not affect he sum.
(a + b) + c = a + (b + c)
Power Rule
Product to Powers
Simplifying Rational Expressions
Factoring Perfect Square Trinomials
Quotient to Powers
evaluating an algebraic expression
find the value of an expression for a given value of the variable
Definition of a1/n
Negative Exponents in Numerators and Denominators
Polynomial in x
set
a collection of objects whose contents can be clearly determined
Principal nth Root of a Real Number
Definition of am/n
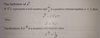
Quotient Rule
Product and Quotient Rules for nth Roots
roster method
the use of braces { } and commas to separate the elements of the set
Union of Sets
the set of elements that are membersof set A or of set B or of both sets. expressed as AUB
Properties of Negatives
Zero Exponent Rule
mathematical models
modeling formulas together with the meaning assigned to the variables
Converting from Decimal to Scientific Notation
Exponential Notation
a counting number raised to the nth power from a base number
Strategy for Factoring a Polynomial
Degree of axn
Important Subsets of the Real Numbers
Order of Operations Agreement
Parenthesis - innermost to outermost Exponents Multiplications and divisions as they occur from left to right Additions and subtractions as they occur from left to right
Absolute Value
Absolute Value Properties
1
Product Rule
Subtraction and Division
Negative Exponent Rule
set-builder notation
the elements of the set are described but not listed (x,y)
Distance Between Two Points on a Number Line
|a - b| = |b-a|
elements
the objects in a set
equation
an equal sign is placed between two algebraic expressions
Multiplying Polynomials When Neither is a Monomial
Strategy for Factoring ax2 + bx + c
Properties of the Real Numbers
1
Product of the Sum and Difference of Two Terms
Irrational Numbers
the set of irrational numbers is the set of all numbers whose decimal representations are neither terminating nor repeating. Irrational numbers cannot be expressed as a quotient of integers.
Example:
algebraic expression
a combination of variables and numbers using the operations of addition, subtraction, multiplication, or division, as well as powers or roots
Whole Numbers
{0,1,2,3,4,5, … }
The set of whole numbers includes 0 and the natural numbers
Example: 0,2,3,5,17
Natural Numbers
{1,2,3,4,5,…} These are the numbers that we use for counting.
Example: 2,3,5,17
Using FOIL to Multiply Binomials
Product Rule for Square Roots
formula
an equation that uses variables to express a relationship between two or more quantities
Scientific Notation
Real Numbers
the set of numbers that are either reational or irrational
Intersection of Sets
the set of elements common to both sets A and B. expressed as
commutative property of multiplication
changing order when multiplying does not affect the product (ab = ba)
Example: x · 6 = 6x
mathematical model breakdown
when a mathematical model gives an estimate that is not a good approximation or is extended to include values of the variable that do not make sense.
mathematical modeling
the process of finding formulas to describe real-world phenomena
Square of a Binomial Sum
Quotient Rule for Square Roots
commutative property of addition
changing order when addeing does not affect the sum (a + b = b + a)
Example: 13+7=7+13
Rational Numbers
{a/b | a and b are integers and b<>0}
The set of rational numbers is the set of all numbers that can be expressed as a quotient of two integers, with the denominator not 0. Rational numbers can be expressed as terminating or repeating decimals.
Example: -17=(-17/1),-5=(-5/1),-3,-2,0,2,3,5,17,
(2/5)=0.4,(-2/3)=-0.6666
Square of a Binomial Difference
Integers
{…,-5,-4,-3,-2,-1,0,1,2,3,4,5,…}
The set of integers includes the negatives of the natural numbers and the whole numbers.
Example: -17,-5,-3,-2,0,2,3,5,17
Multiplying Rational Expressions
Principal Square Root
