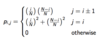Concepts and Rules Flashcards
Binomial Distribution for Population Genetics
Genotype Number
NAA ~ Bi(N, (fA)2)
E(NAA) = N(fA)2
E(fAA) = (fA)2
Var(fAA) = (fA)2(1-(fA)2)/N
Large Population Assumption
When N is large enough, the variability in fAA, fAa, faa due to chance will be negligible
Hardy-Weinburg Equilibrium
Under the assumptions: random mating, large population size, no mutation, no selection and no migration
- Allele frequencies never change
- After 1 generation, genotype frequencies don’t change and have the ratios AA:Aa:aa = p2:2pq:q2
fA= p , fa= q
Including Sexual Reproduction
Allele frequency change over the first generation and become an average of the initial male and female pools. They are constant from generation 1 onwards. Genotype frequencies are constant from generation 2 onwards.
Irreversible Mutation
Allele frequencies change over time (A decreases, a increases).
Genotypes are in HW each generation (but with changing p and q).
First Order Difference Equation
Equation which gives the n + 1th term of a sequence in terms of the nth term.
Qualitative behaviour of homogenous difference equations
a>1, xn grows exponentially
a=1, xn = C a constant
0 < a < 1, xn decays exponentially
a = 0, xn = 0, a constant solution independent of x0
-1 < a < 0, xn decays monotonically but xn changes sign, converges with oscillation
a= -1, xn = (-1)nx0, xn oscillates with no decay: diverges with bound oscillation
a < -1, xn diverges with unbounded oscillation monotonically
What is a cobweb diagram?
A graphical method of determining stability
Graph y = xn and y = g(x) where g(x) = xn + 1 on a graph of xn + 1 vs xn
Draw line vertically to g(x) and cobweb!
What are the equilibria of the hardy-weinburg equilibrium?
Every value for fAn+1 is an equilibrium as fAn+1 = fAn
What is the basin of attraction?
The set of all initial conditions whose solutions approach the equilibrium in the limit.
What is the linear stability criterion?
When a tangent line approximation is made (the curve y = g(x) is approximated by its tangent at that point) and teh instantaneous gradient is found:
If |g(x*)| < 1 then x* is stable
If |g(x*)| > 1 then x* is unstable
If |g(x*)| = 1 then the linear stability criterion is inconclusive
How are X - linked genes modelled?
Both male and female gene pools are considered.
fAf(n+1) = 1/2[fAf(n) + fAf(n-1)]
using fAm(n) = fAf(n-1) (lagging females by one generation)
A second order difference equation
The general solution is:
fAf(n) = c1 + c2(-1/2)n
where c1 and c2 are constants that can be found using initial conditions
How is selection modeled?
We use different quantities to distinguish which part of the life cycle we are at:
fA(n), fAA(n) etc for the zygotes
pA(n), pAA(n) etc for the adults about to mate
assume all genotypes have the same fertility, but each has a different, constant viability, giving a constant overall fitness:
wAA, wAa, waa
where wAA is the fraction of AA zygotes that survive to mate
population size can change from generation to generation
What is the Fisher-Haldane-Wright equation?
pA(n + 1) = wAApA(n)2 + wAapA(n)[1 − pA(n)]
wmean
which can be written solely in terms of pA(n)
What is mean fitness?
What is the model for lethal recessive genes?
wAA = wAa
waa = 0
pa(n+1) = pa(n) / (1 + pa(n))
solution
pa(n) = p0 / (1 + np0)
What is relative fitness?
The proportion of fitness compared to the fitness of AA
What is the selection coeficient?
Determines how much fitter AA is compared to aa
What is the heterozygous effect?
Compares fitness of Aa to that of aa
hs is selection pressure against Aa
What are the attributes of dominance?
If A is completely dominant
wAA = wAa > waa
h = 0
If a is completely dominant
wAa = waa < wAA
h = 1
What are the attributes of incomplete dominance?
wAA > wAa >waa
0 < h < 1
called directed selection.
What are the attributes of codominance?
Two possibilities:
- wAa > wAA ≥ waa
h < 0, heterozygote advantage
- wAa < waa ≤ wAA
h > 1, hetorozygote disadvantage
What is the FHW in terms of h and s?
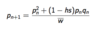
What are the equilibrium solutions of the FHW equation?
p* = 0 (no A)
p* = 1 (A is fixed)
p* = (h - 1)/(2h-1) =P if h is not 1/2
What happens in directed selection?
As 0<h></h>
<p>p* = 0 is unstable</p>
<p>p* = 1 is stable</p>
<p>So A increases, eventually becoming fixed while a becomes extinct</p>
</h>
What happens in heterozygote advantage?
h < 0
All three equilibria are applicable
P = (h - 1)/(2h - 1) is a stable equilibrium
0, 1 are unstable - no fixation or extinction
The population reaches a stable equilibrium with both A and a present.
What happens in heterozygote disadvantage?
h > 1
all three equilibria are applicable
P = (h-1)/(2h-1) is unstable
0, 1 are both stable
long term result depends on initial conditions
- if p0 < P then pn approaches 0
- if p0 > P then pn approaches 1
What is the Wright-Fisher Model?
A model for population genetics in small population where NA(n) = i and generation n+1 is produced by 2N independent random samples from the allele pool, with probability of success i/2N
Markov chains are used to calculate the probabilities of different values of i
What is a Markov Chain?
A markov chain is a process that is described by a sequence of random variables
Fixed Set S
probabilities for X(n+1) depend only on the value of X(n) and are independent of n
What is a Monte Carlo Simulation?
A simulation where all possible paths to get to a particular destination are taken into account to get a frequency distribution and approximate the probability mass function.
What is Genetic Drift?
Under the Wright-Fisher Model (Where N is small), the number of A alleles in a gene pool either goes to 0 (extinction) or goes to 2N (fixation) just due to random sample.
Fluctuations in NA can cause extinction/fixation in finite time just by chance.
What is the Moran Model?
The Moran model is a model for small populatio population genetics that considers a haploid population of size N
At each step, one allele is chosen to reproduce, one to die (with replacement). This creates a Markov Chain.
What is Heterozygosity?
The probability that two randomly sampled alleles from generation n will be different.
Also tells us the expected frequency of heterozygotes
