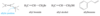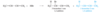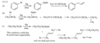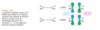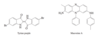Conjugated Systems, Orbital Symmetry, and Ultraviolet Spectroscopy Flashcards
Define:
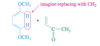
Conjugated
Double bonds can interact with each other if they are separated by just one single bond. Such interacting double bonds are said to be conjugated.
Define:
Isolated Double Bonds
Double bonds with two or more single bonds separating them have little interaction and are called isolated double bonds.
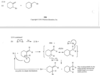
For example, penta-1,3-diene has conjugated double bonds, while penta-1,4-diene has isolated double bonds.
Which is more stable conjugated or isolated double bonds?
Because of the interaction between the double bonds, systems containing conjugated double bonds tend to be more stable than similar systems with isolated double bonds.
What is the heat of hydrogenation of molecules with two isolated double bonds?
When a molecule has two isolated double bonds, the heat of hydrogenation is close to the sum of the heats of hydrogenation for the individual double bonds. For example, the heat of hydrogenation of penta-1,4-diene is -252 kJ/mol (-60.2 kcal/mol), about twice that of pent-1-ene.
What is the head of hydrogenation for conjugated dienes?
For conjugated dienes, the heat of hydrogenation is less than the sum for the individual double bonds. For example, trans-penta-1,3-diene has a monosubstituted double bond like the one in pent-1-ene and a disubstituted double bond like the one in pent-2-ene. The sum of the heats of hydrogenation of pent-1-ene and pent-2-ene is -242 kJ (-57.7 kcal), but the heat of hydrogenation of trans-penta-1,3-diene is only -225 kJ/mol (-53.7 kcal/mol), showing that the conjugated diene has about 17 kJ/mol (4.0 kcal/mol) extra stability.
What happens if two double bonds are even closer together than in the conjugated case?
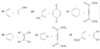
Successive double bonds with no intervening single bonds are called cumulated double bonds. Consider penta-1,2-diene, which contains cumulated double bonds. Such 1,2-diene systems are also called allenes, after the simplest member of the class, propa- 1,2-diene or “allene,” H2C = C = CH2. The heat of hydrogenation of penta-1,2-diene is is -292 kJ/mol (-69.8 kcal/mol), a larger value than any of the other pentadienes.
How stable are cumulated double bonds when compared to the other double bond structures?
Because penta-1,2-diene has a larger heat of hydrogenation than penta-1,4-diene, we conclude that the cumulated double bonds of allenes are less stable than isolated double bonds and much less stable than conjugated double bonds.
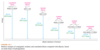
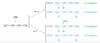
Rank each group of compounds in order of increasing heat of hydrogenation.
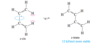
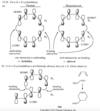
In a strongly acidic solution, cyclohexa-1,4-diene tautomerizes to cyclohexa-1,3-diene. Propose a mechanism for this rearrangement, and explain why it is energetically favorable.
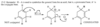
The central carbon atom of an allene is a member of two double bonds, and it has an interesting orbital arrangement that holds the two ends of the molecule at right angles to each other.
(a) Draw an orbital diagram of allene, showing why the two ends are perpendicular.
(b) Draw the two enantiomers of penta-2,3-diene.
What is the name used to describe the extra stability found in conjugated molecules?
This extra stability in the conjugated molecule is called the resonance energy of the system. (Other terms favored by some chemists are conjugation energy, delocalization energy, and stabilization energy.)
Describe the Heat of Hydrogenation of buta-1,3-diene.
The heat of hydrogenation of buta-1,3-diene is about 17 kJ/mol (4.0 kcal/mol) less than twice that of but-1-ene, showing that buta-1,3-diene has a resonance energy of 17 kJ/mol.
What is the most stable configuration of buta-1,3-diene?
The configuartion is planar with the p orbitals on the two pi bonds aligned.
The C2¬C3 bond in buta-1,3-diene (1.48 Å) is shorter than a carbon–carbon single bond in an alkane (1.54 Å). This bond is shortened slightly by the increased s character of the sp2 hybrid orbitals, but the most important cause of this short bond is its pi bonding overlap and partial double-bond character. The planar conformation, with the p orbitals of the two double bonds aligned, allows overlap between the pi bonds. In effect, the electrons in the double bonds are delocalized over the entire molecule, creating some pi overlap and pi bonding in the C2 ¬ C3 bond. The length of this bond is intermediate between the normal length of a single bond and that of a double bond.
Why do we draw plus/minuses on orbitals?
The plus and minus signs used in drawing these orbitals indicate the phase of the wave function, not electrical charges.
How do the orbitals of ethylene interact with each other?
In the pi bonding molecular orbital of ethylene, the lobes that overlap in the bonding region between the nuclei are in phase; that is, they have the same sign ( + overlaps with +, and - overlaps with -). We call this reinforcement constructive overlap. Constructive overlap is an important feature of all bonding molecular orbitals.
In the pi antibonding molecular orbital (marked by *), on the other hand, lobes of opposite phase (with opposite signs, + with -) overlap in the bonding region. This destructive overlap causes cancelling of the wave function in the bonding region. Midway between the nuclei, this antibonding MO has a node: a region of zero electron density where the positive and negative phases exactly cancel.
Blue = Plus Phase; Green = Minus Phase
What are the energies of the bonding and antibonding MOs?
Electrons have lower energy in the bonding MO than in the original p orbitals, and higher energy in the antibonding MO. In the ground state of ethylene, two electrons are in the bonding MO, but the antibonding MO is vacant. Stable molecules tend to have filled bonding MOs and empty antibonding MOs.
Describe the important principles illustrated in the figure.
Constructive overlap results in a bonding interaction; destructive overlap results in an antibonding interaction. Also, the number of molecular orbitals is always the same as the number of atomic orbitals used to form the MOs. These molecular orbitals have energies that are symmetrically distributed above and below the energy of the starting p orbitals. Half are bonding MOs, and half are antibonding MOs.
How would you describe buta-1,3-diene’s pi bonding orbitals design (constructive)?
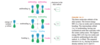
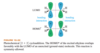
The lowest-energy molecular orbital always consists entirely of bonding interactions. We indicate such an orbital by drawing all the positive phases of the p orbitals overlapping constructively on one face of the molecule, and the negative phases overlapping constructively on the other face. Figure 15-4 shows the lowest-energy MO for buta-1,3-diene. This MO places electron density on all four p orbitals, with slightly more on C2 and C3. (In these figures, larger and smaller p orbitals are used to show which atoms bear more of the electron density in a particular MO.)
How would you describe buta-1,3-diene second pi bonding orbitals design (semiconstructive)?
As with ethylene, the second molecular orbital (π2) of butadiene has one vertical node in the center of the molecule. This MO represents the classic picture of a diene. There bonding interactions at the C1 - C2 and C3 - C4 bonds, and (weaker) antibonding interaction between C2 and C3.
Why would you subtract the number of bonding and antibonding orbitals?
The π2 orbital has two bonding interactions and one anti-bonding interaction, so we expect it to be a bonding orbital (2 bonding - 1 antibonding = 1 bonding). It is not as strongly bonding nor as low in energy as the all-bonding p1 orbital. Adding and subtracting bonding and antibonding interactions is not a reliable method for calculating energies of molecular orbitals, but it is useful for predicting whether a given orbital is bonding or antibonding and for ranking orbitals in order of their energy.
How would you describe buta-1,3-diene’s third pi bonding orbital design (semidestructive)?
The third butadiene MO (π3*) has two nodes (Figure 15-6). There is a bonding interaction at the C2 - C3 bond, and there are two antibonding interactions, one between C1 and C2 and the other between C3 and C4. This an antibonding orbital (*), and it is vacant in the ground state.
How you describe buta-1,3-diene’s fourth pi bonding orbital design (destructive)?
The fourth, and last, molecular orbital (π4*) of buta-1,3-diene has three nodes and is totally antibonding (Figure 15-7). This MO has the highest energy and is unoccupied in the molecule’s ground state. This highest-energy MO (π4*) is typical: For most systems, the highest-energy MO has antibonding interactions between all pairs of adjacent atoms.
Why is buta-1,3-diene is most stable in the planar conformation?
The partial double-bond character between C2 and C3 in buta-1,3-diene explains why the molecule is most stable in a planar conformation. There are actually two planar conformations that allow overlap between C2 and C3. These conformations arise by rotation about the C2 ¬ C3 bond, and they are considered single-bond analogues of trans and cis isomers about a double bond. Thus, they are named s-trans (“single”-
trans) and s-cis (“single”-cis) conformations.
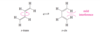
Describe the stabilities between the s-trans and s-cis conformations of buta-1,3,-diene? Against an alkene?
The s-trans conformation is 12 kJ/mol (2.8 kcal/mol) more stable than the s-cis conformation, which whows interference betweent two nearby hydrogen atoms. The barrier for rotation about the C2 - C3 bond from s-trans to s-cis) is only about 29 kJ/mol (about 7 kcal/mol) compared with about 250 kJ/mol (60 kcal/mol) for rotation of a double bond in an alkene. The s-cis and s-trans conformers of butadiene (and all the skew conformations in between) easily interconvert at room temperature.
What type of reactions do conjugated compounds typically undergo?
Conjugated compounds undergo a variety of reactions, many of which involve intermediates that retain some of the resonance stabilization of the conjugated system. Common intermediates include allylic systems, particularly allylic cations and radicals. Allylic cations and radicals are stabilized by delocalization.
Define:
Allyl Group
The – CH2 – CH = CH2 group is called the allyl group. Many common names use this terminology.
When is allyl bromide often used?
When allyl bromide is heated with a good ionizing solvent, it ionizes to the allyl cation, an allyl group with a positive charge. More-substituted analogues are called allylic cations. All allylic cations are stabilized by resonance with the adjacent double bond, which delocalizes the positive charge over two carbon atoms.
Draw another resonance form for each of the substituted allylic cations shown in the preced- ing figure, showing how the positive charge is shared by another carbon atom. In each case, state whether your second resonance form is a more important or less important resonance contributor than the first structure. (Which structure places the positive charge on the more- substituted carbon atom?)
When 3-bromo-1-methylcyclohexene undergos solvolysis in hot ethanol, two products are formed. Propose a mechanism that accounts for both of these products.
How can you represent the delocalization of the positive charge on an allyl cation?
We can represent a delocalized ion such as the allyl cation either by resonance forms, as shown on the left in the following figure, or by a combined structure, as shown on the right. Although the combined structure is more concise, it is sometimes confusing because it attempts to convey all the information implied by two or more resonance forms.
How stable is an allyl cation?
Because of its resonance stabilization, the (primary) allyl cation is about as stable as a simple secondary carbocation, such as the isopropyl cation. Most substituted allylic cations have at least one secondary carbon atom bearing part of the positive charge. They are about as stable as simple tertiary carbocations such as the tert-butyl cation.
What occurs betweent the reaction of HBr and buta-1,3-diene?
Electrophilic additions to conjugated dienes usually involve allylic cations as intermediates. Unlike simple carbocations, an allylic cation can react with a nucleophile at either of its positive centers. Let’s consider the addition of HBr to buta-1,3-diene, an electrophilic addition that produces a mixture of two constitutional isomers. One product, 3-bromobut-1-ene, results from Markovnikov addition across one of the double bonds. In the other product, 1-bromobut-2-ene, the double bond shifts to the C2 ¬ C3 position.
How would you get the frist prodcut from the electrophilic addtion of HBr?
The first product results from electrophilic addition of HBr across a double bond. This process is called a 1,2-addition whether or not these two carbon atoms are numbered 1 and 2 in naming the compound. In the second product, the proton and bromide ion add at the ends of the conjugated system to carbon atoms with a 1,4-relationship. Such an addition is called a 1,4-addition whether or not these carbon atoms are numbered 1 and 4 in naming the compound.
Describe the Mechanism for 1,2- and 1,4-Addition to a Conjugated Diene?
The mechanism is similar to other electrophilic additions to alkenes. The proton is the electrophile, adding to the alkene to give the most stable carbocation. Protonation of buta-1,3-diene gives an allylic cation, which is stabilized by resonance delocalization of the positive charge over two carbon atoms. Bromide can attack this resonance-stabilized intermediate at either of the two carbon atoms sharing the positive charge. Attack at the secondary carbon gives 1,2-addition; attack at the primary carbon gives 1,4-addition.
Treatment of an alkyl halide with alcoholic AgNO3 often promotes ionization.
Ag+ + R – Cl –> AgCl + R+
When 4-chloro-2-methylhex-2-ene reacts with AgNO3 in ethanol, two isomeric ethers are formed. Suggest structures, and propose a mechanism for their formation.
Propose a mechanism for each reaction, showing explicitly how the observed mixtures of products are formed.
How does temperature affect the buta-1,3-diene reation with HBr?
One of the interesting peculiarities of the reaction of buta-1,3-diene with HBr is the effect of temperature on the products. If the reagents are allowed to react briefly at - 80 °C, the 1,2-addition product predominates. If this reaction mixture is later allowed to warm to 40 °C, however, or if the original reaction is carried out at 40 °C, the composition favors the 1,4-addition product.
Why isn’t the most stable compounds always the one the predominates (buta-1,3-diene + HBr)?
This variation in product composition reminds us that the most stable product is not always the major product. Of the two products, we expect 1-bromobut-2-ene (the 1,4-product) to be more stable, since it has the more substituted double bond. This prediction is supported by the fact that this isomer predominates when the reaction mixture is warmed to 40 °C and allowed to equilibrate.
A reaction-energy diagram for the second step of this reaction (Figure 15-9) helps to show why one product is favored at low temperatures and another at higher temperatures. The allylic cation is in the center of the diagram; it can react toward the left to give the 1,2-product or toward the right to give the 1,4-product. The initial product depends on where bromide attacks the resonance-stabilized allylic cation. Bromide can attack at either of the two carbon atoms that share the positive charge. Attack at the secondary carbon gives 1,2-addition, and attack at the primary carbon gives 1,4-addition.
How can temperature be used to kinetically control the products of buta-1,3-diene and HBr to favor 1,2-addition?
The transition state for 1,2-addition has a lower energy than transition state for 1,4-addition. This is not surprising, because 1,2-addition results from bromide attack at the a more substituted secondary carbon, which bears more of the positive charge because it is better stabilized than the primary carbon. Because the 1,2-addition has a lower activation energy than the 1,4-addition, the 1,2-addition takes place faster (at all temperatures).
Attack by bromide on the allylic cation is a strongly exothermic process, so the reverse reaction has a large activation energy. At -80 °C, few collisions take place with this much energy, and the rate of the reverse reaction is practically zero. Under these conditions, the product that is formed faster predominates. Because the kinetics of the reaction determine the results, this situation is called kinetic control of the reaction. The 1,2-product, favored under these conditions, is called the kinetic product.
How can temperature be used in th buta-1,3-diene and HBr reaction to favor 1,4-addition?
At 40 °C, a significant fraction of molecular collisions have enough energy for reverse reactions to occur. Notice that the activation energy for the reverse of the 1,2-addition is less than that for the reverse of the 1,4-addition. Although the 1,2-product is still formed faster, it also reverts to the allylic cation faster than the 1,4-product does. At 40 °C, an equilibrium is set up, and the relative energy of each species determines its concentration. The 1,4-product is the most stable species, and it predominates. Since thermodynamics determine the results, this situation is called thermodynamic control (or equilibrium control) of the reaction. The 1,4-product, favored under these conditions, is called the thermodynamic product.
What is the relationship between kinetics and thermodynamics to reversability?
In general, reactions that do not reverse easily are kinetically controlled because no equilibrium is established. In kinetically controlled reactions, the product with the lowest-energy transition state predominates. Reactions that are easily reversible are thermodynamically controlled unless something happens to prevent equilibrium from being attained. In thermodynamically controlled reactions, the lowest-energy product predominates.
When Br2 is added to buta-1,3-diene at -15°C, the product mixture contains 60% of the product A and 40% of product B. When the same reaction takes place at 60°C, the product ratio is 10% A and 90% B.
Describe the Mechanism for a Free-Radical Allylic Bromination.
Why is it that (in the first propagation step) a bromine radical abstracts only an allylic hydrogen atom, and not one from another secondary site?
Abstraction of allylic hydrogens is preferred because the allylic free radical is resonance-stabilized. The bond-dissociation enthalpies required to generate several free radicals are compared below. Notice that the allyl radical (a primary free radical) is actually 13 kJ/mol (3 kcal/mol) more stable than the tertiary butyl radical.
What products will result from this free radical bromination? What product would result in a less symmetrical allyl?
The allylic cyclohex-2-enyl radical has its unpaired electron delocalized over two secondary carbon atoms, so it is even more stable than the unsubstituted allyl radical. The second propagation step may occur at either of the radical carbons, but in this symmetrical case, either position gives 3-bromocyclohexene as the product. Less symmetrical compounds often give mixtures of products resulting from an allylic shift: In the product, the double bond can appear at either of the positions it occupies in the resonance forms of the allylic radical. An allylic shift in a radical reaction is similar to the 1,4-addition of an electrophilic reagent such as HBr to a diene.
When methylenecyclohexane is treated with a low concentration of bromine under irradiation by a sunlamp, two substitution products are formed.
At higher concentrations, bromine add accross double bonds (via a bromonium ion) to give saturated dibromides (sections 8-8). How can this be overcomed?
In the allylic bromination just shown, bromine substitutes for a hydrogen atom. The key to getting substitution is to have a low concentration of bromine, together with light or free radicals to initiate the reaction. Free radicals are highly reactive, and even a small concentration of radicals can produce a fast chain reaction.
Simply adding bromine might raise the concentration too high, resulting in ionic addition of bromine across the double bond. A convenient bromine source for allylic bromination is N-bromosuccinimide (NBS), a brominated derivative of succinimide. Succinimide is a cyclic imide (diamide) of the four-carbon diacid succinic acid.
NBS provides a fairly constant, low concentration of Br2 because it reacts with HBr liberated in the substitution, converting it back into Br2. This reaction also removes the HBr by-product, preventing it from adding across the double bond by its own free-radical chain reaction.
When N-bromosuccinimide is added to hex-1-ene in CCl4 and a sunlamp is shone on the mixture, three products result.
- (a) Give the structures of these three products.
- (b) Propose a mechanism that accounts for the formation of these three products.
Predict the product(s) of light-initiated reaction with NBS in CCl4 for the following starting materials.
Describe the electronic structure of allylic systems using allyl radicals.
Let’s take a closer look at the electronic structure of allylic systems, using the allyl radical as our example. One resonance form shows the radical electron on C1, with a pi bond between C2 and C3. The other shows the radical electron on C3 and a pi bond between C1 and C2. These two resonance forms imply that there is half a pi bond between C1 and C2 and half a pi bond between C2 and C3, with the radical electron half on C1 and half on C3.
Do resonance structure exist co- or independently of each other ? [Use allyl radical as example]
Remember that no resonance form has an independent existence: A compound has characteristics of all its resonance forms at the same time, but it does not “resonate” among them. The p orbitals of all three carbon atoms must be parallel to have simultaneous pi bonding overlap between C1 and C2 and between C2 and C3. The geometric structure of the allyl system is shown in Figure 15-10. The allyl cation, the allyl radical, and the allyl anion all have this same geometric structure, differing only in the number of pi electrons.
Describe the molecular orbitals of the allyl radical system?
Just as the four p orbitals of buta-1,3-diene overlap to form four molecular orbitals, the three atomic p orbitals of the allyl system overlap to form three molecular orbitals, shown in Figure 15-11. These three MOs share several important features with the MOs of the butadiene system. The first MO is entirely bonding, the second has one node, and the third has two nodes and (because it is the highest-energy MO) is entirely antibonding.
As with butadiene, we expect that half of the MOs will be bonding, and half antibonding; but with an odd number of MOs, they cannot be symmetrically divided. One of the MOs must appear at the middle of the energy levels, neither bonding nor antibonding: It is a nonbonding molecular orbital. Electrons in a nonbonding orbital have the same energy as in an isolated p orbital.
The structure of the nonbonding orbital (π2) may seem strange because there is zero electron density on the center p-orbital (C2). This is the case because π2 must have one node, and the only symmetrical position for one node is in the center of the molecule, crossing C2. We can tell from its structure that π2 must be nonbonding, because C1 and C3 both have zero overlap with C2. The total is zero bonding, implying a nonbonding orbital.
Addition of 1-bromobut-2-ene to magnesium metal in dry ether results in formation of a Grignard reagent. Addition of water to this Grignard reagent gives a mixture of but-1-ene and but-2-ene (cis and trans). When the Grignard reagent is made using 3-bromobut-1-ene, addition of water produces exactly the same mixture of products in the same ratios. Explain this curious result.
How reactive are allylic halides and tosylates? Why is this?
Allylic halides and tosylates show enhanced reactivity toward nucleophilic displacement reactions by the SN2 mechanism. For example, allyl bromide reacts with nucleophiles by the SN2 mechanism about 40 times faster than n-propyl bromide.
Figure 15-13 shows how this rate enhancement can be explained by allylic delocalization of electrons in the transition state. The transition state for the SN2 reaction looks like a trigonal carbon atom with a p orbital perpendicular to the three substituents. The electrons of the attacking nucleophile are forming a bond using one lobe of the p orbital while the leaving group’s electrons are leaving from the other lobe. When the substrate is allylic, the transition state receives resonance stabilization through conjugation with the p orbitals of the pi bond. This stabilization lowers the energy of the transition state, resulting in a lower activation energy and an enhanced rate.
The enhanced reactivity of allylic halides and tosylates makes them particularly attractive as electrophiles for SN2 reactions. They are so reactive that they are with which reagents?
Allylic halides are so reactive that they couple with Grignard and organolithium reagents, a reaction that does not work well with unactivated halides.
Show how you might synthesize the following compounds starting with alkyl, alkenyl, or aryl halides containing four carbon atoms or fewer.
- (a) 3-phenylprop-1-ene
- (b) 5-methylhex-2-ene
- *(c) dec-5-ene
Define:
Diels-Alder Reaction
In 1928, German chemists Otto Diels and Kurt Alder discovered that alkenes and alkynes with electron-withdrawing groups add to conjugated dienes to form six-membered rings. The Diels–Alder reaction has proven to be a useful synthetic tool, providing one of the best ways to make six-membered rings with diverse functionality and controlled stereochemistry. Diels and Alder were awarded the Nobel Prize in 1950 for their work.
Describe the Diels-Alder Reaction
The Diels–Alder reaction is called a [4 + 2] cycloaddition because a ring is formed by the interaction of four pi electrons in the diene with two pi electrons of the alkene or alkyne. Since the electron-poor alkene or alkyne is prone to react with a diene, it is called a dienophile (“lover of dienes”). In effect, the Diels–Alder reaction converts two pi bonds into two sigma bonds. We can symbolize the Diels–Alder reaction by using three arrows to show the movement of three pairs of electrons. This electron movement is concerted, with three pairs of electrons moving simultaneously.
The Diels–Alder reaction is like a nucleophile–electrophile reaction. The diene is electron-rich, and the dienophile is electron-poor. Simple dienes such as buta-1,3-diene are sufficiently electron-rich to be effective dienes for the Diels–Alder reaction. The presence of electron-donating ( – D) groups, such as alkyl groups or alkoxy ( – OR) groups, may further enhance the reactivity of the diene.
Predict the products of the following proposed Diels-Alder reactions.
What dienes and dienophiles would react to give the following Diels-Alder prodcuts?
What role does geometry play in the Diels-Alder reaction?
The mechanism of the Diels–Alder reaction is a concerted cyclic movement of six electrons: four in the diene and two in the dienophile. For the three pairs of electrons to move simultaneously, the transition state must have a geometry that allows overlap of the two end p orbitals of the diene with those of the dienophile. Figure 15-15 shows the required geometry of the transition state. The geometry of the Diels–Alder transition state explains why some isomers react differently from others, and it enables us to predict the stereochemistry of the products.
Describe the s-cis Conformation of the Diene.
The diene must be in the s-cis conformation to react. When the diene is in the s-tran conformation, the end p orbitals are too far apart to overlap with the p orbitals of the dienophile. The s-trans conformation usually has a lower energy than the s-cis, but this energy difference is not enough to prevent most dienes from undergoing Diels-Alder reactions. For example, the s-trans conformation of butadiene is only 9.6 kJ/mol (2.3 kcal/mol) lower in energy than the s-cis conformation.
What affects to s inducing features have on Diels-Alder reactions?
Structural features that aid or hinder the diene in achieving the s-cis conformation affect its ability to participate in Diels–Alder reactions. Figure 15-16 shows that dienes with functional groups that hinder the s-cis conformation react more slowly than butadiene. Dienes with functional groups that hinder the s-trans conformation react faster than butadiene.
What features characterize cyclopentadiene for Diels-Alder reaction?
Because cyclopentadiene is fixed in the s-cis conformation, it is highly reactive in the Diels–Alder reaction. It is so reactive, in fact, that at room temperature, cyclopentadiene slowly reacts with itself to form dicyclopentadiene. Cyclopentadiene is regenerated by heating the dimer above 200 °C. At this temperature, the Diels–Alder reaction reverses, and the more volatile cyclopentadiene monomer distills over into a cold flask. The monomer can be stored indefinitely at dry-ice temperatures.
What is the stereochemistry of a Diels-Alder reaction?
The Diels–Alder reaction is a syn addition with respect to both the diene and the dienophile. The dienophile adds to one face of the diene, and the diene adds to one face of the dienophile. As you can see from the transition state in Figure 15-15, there is no opportunity for any of the substituents to change their stereochemical positions during the course of the reaction. Substituents that are on the same side of the diene or dienophile will be cis on the newly formed ring. The following examples show the results of this syn addition.
Define:
The Endo Rule
When the dienophile has a pi bond in its electron-withdrawing group (as in a carbonyl group or a cyano group), the p orbitals in that electron-withdrawing group approach one of the central carbon atoms (C2 or C3) of the diene. This proximity results in secondary overlap: an overlap of the p orbitals of the electron-withdrawing group with the p orbitals of C2 and C3 of the diene (Figure 15-17). Secondary overlap helps to stabilize the transition state.
The influence of secondary overlap was first observed in reactions using cyclopentadiene to form bicyclic ring systems. In the bicyclic product (called norbornene), the electron-withdrawing substituent occupies the stereochemical position closest to the central atoms of the diene. This position is called the endo position because the substituent seems to be inside the pocket formed by the six-membered ring of norbornene. This stereochemical preference for the electron-withdrawing substituent to appear in the endo position is called the endo rule.
Use the endo rule to predict the product of the following cycloaddition.
Predict the major product for each proposed DIels-Alder reaction. Include stereochemistry where appropriate.
How do Diels-Alder reactions proceed when using unsymmetrical reagents?
Even when the diene and dienophile are both unsymmetrically substituted, the Diels–Alder reaction usually gives a single product (or a major product) rather than a random mixture. We can usually predict the major product by considering how the substituents polarize the diene and the dienophile in their charge-separated resonance forms. If we then arrange the reactants to connect the most negatively charged carbon in the (electron-rich) diene with the most positively charged carbon in the (electron-poor) dienophile, we can usually predict the correct orientation. The following examples show that an electron-donating substituent (D) on the diene and an electron-withdrawing substituent (W) on the dienophile usually show either a 1,2- or 1,4-relationship in the product.
In most cases, we don’t even need to draw the charge-separated resonance forms to determine which orientation of the reactants is preferred. We can predict the major products of unsymmetrical Diels–Alder reactions simply by remembering that the electron-donating groups of the diene and the electron-withdrawing groups of the dienophile usually bear either a 1,2-relationship or a 1,4-relationship in the products, but not a 1,3-relationship.
Predict the products of the following proposed Diels-Alder reactions.
Draw the charge-separated resonance forms of the reactants to support these predictions.
Predict the products of the following Diels-Alder reactions.
Define:
Cycloaddition
The Diels–Alder reaction is a cycloaddition: Two molecules combine in a one-step, concerted reaction to form a new ring. Cycloadditions such as the Diels–Alder are one class of pericyclic reactions, which involve the concerted forming and breaking of bonds within a closed ring of interacting orbitals. Figure 15-15 (page 686) shows the closed loop of interacting orbitals in the Diels–Alder transition state. Each carbon atom of the new ring has one orbital involved in this closed loop.
Pericyclic reactions were intially poorly understood. Why is this?
For many years, pericyclic reactions were poorly understood and unpredictable. Around 1965, Robert B. Woodward and Roald Hoffmann developed a theory for predicting the results of pericyclic reactions by considering the symmetry of the molecular orbitals of the reactants and products. Their theory, called conservation of orbital symmetry, says that the molecular orbitals of the reactants must flow smoothly into the MOs of the products without any drastic changes in symmetry. In that case, there will be bonding interactions to help stabilize the transition state. Without these bonding interactions in the transition state, the activation energy is much higher, and the concerted cyclic reaction cannot occur. Conservation of symmetry has been used to develop “rules” to predict which pericyclic reactions are feasible and what products will result. These rules are often called Woodward-Hoffmann rules.
Define:
Highest Occupied Molecular Orbital (HOMO)
In the Diels–Alder reaction, the diene acts as the electron-rich nucleophile, and the dienophile acts as the electron-poor electrophile. If we imagine the diene contributing a pair of electrons to the dienophile, the highest-energy electrons of the diene require the least activation energy for such a donation. The electrons in the highest-energy occupied orbital, called the Highest Occupied Molecular Orbital (HOMO), are the important ones because they are the most weakly held. The HOMO of butadiene is π2, and its symmetry determines the course of the reaction.
Define:
Lowest Unoccupied Molecular Orbital (LUMO)
The orbital in ethylene that receives these electrons is the lowest-energy orbital available, the Lowest Unoccupied Molecular Orbital (LUMO). In ethylene, the LUMO is the π* antibonding orbital. If the electrons in the HOMO of butadiene can flow smoothly into the LUMO of ethylene, a concerted reaction can take place.
What role does the HOMO and LUMO of butadiene and ethylene play in their Diels-Alder reaction?
Figure 15-19 shows that the HOMO of butadiene has the correct symmetry to overlap in phase with the LUMO of ethylene. Having the correct symmetry means the orbitals that form the new bonds can overlap constructively: plus with plus and minus with minus. These bonding interactions stabilize the transition state and promote the concerted reaction. This favorable result predicts that the reaction is symmetry-allowed. The Diels–Alder reaction is common, and this theory correctly predicts a favorable transition state.
Define:
Symmetry-Forbidden
If a cycloaddition produces an overlap of positive-phase orbitals with negative-phase orbitals (destructive overlap), antibonding interactions are generated. Antibonding interactions raise the activation energy, so the reaction is classified as symmetry-forbidden. The thermal [2 + 2] cycloaddition of two ethylenes to give cyclobutane is a symmetry-forbidden reaction.
This [2 + 2] cycloaddition requires the HOMO of one of the ethylenes to overlap with the LUMO of the other. Figure 15-20 shows that an antibonding interaction results from this overlap, raising the activation energy. For a cyclobutane molecule to result, one of the MOs would have to change its symmetry. Orbital symmetry would not be conserved, so the reaction is symmetry-forbidden. Such a symmetry-forbidden reaction can occasionally be made to occur, but it cannot occur in the concerted pericyclic manner shown in the figure.
How does switching between heat to ultraviolet light effect pericyclic reactions?
When ultraviolet light rather than heat is used to induce pericyclic reactions, our predictions generally must be reversed. For example, the [2 + 2] cycloaddition of two ethylenes is photochemically “allowed.” When a photon with the correct energy strikes ethylene, one of the pi electrons is excited to the next higher molecular orbital (Figure 15-21). This higher orbital, formerly the LUMO, is now occupied: It is the new HOMO*, the HOMO of the excited molecule.
The HOMO* of the excited ethylene molecule has the same symmetry as the LUMO of a ground-state ethylene. An excited molecule can react with a ground-state molecule to give cyclobutane (Figure 15-22). The [2 + 2] cycloaddition is therefore photochemically allowed but thermally forbidden. In most cases, photochemically allowed reactions are thermally forbidden, and thermally allowed reactions are photochemically forbidden.
Show that the [4 + 2] Diels-Alder reaction is photochemically forbidden.
- (a) Show that the [4 + 4] cycloaddtion of two butadiene molecules to give cycloocta-1,5-diene is thermally forbidden but photochemically allowed.
- (b) There is a different, thermally allowed cycloaddition of two butadiene molecules. Show this reaction, and explain why it is thermally allowed. (Hint: Consider the dimerization of cyclopentadiene.)
How can photons affect the electronic structure of ethylene?
Ethylene, for example, has two pi orbitals: the bonding orbital (π, the HOMO) and the antibonding orbital (π*, the LUMO). The ground state has two electrons in the bonding orbital and none in the antibonding orbital. A photon with the right amount of energy can excite an electron from the bonding orbital (π) to the antibonding orbital (π*). This transition from a p bonding orbital to a π* antibonding orbital is called π –> π* trainsition (Figure 15-23).
What are the energy differences between ethylene and butadiene HOMO/LUMO?
The π –> π* transition of ethylene requires absorption of light at 171 nm (686 kJ/mol). Most UV spectrometers cannot detect this absorption because it is obscured by the absorption caused by oxygen in the air. In conjugated systems, however, there are electronic trainsitions with lower energies that correspond to wavelengths longer than 200 nm. Figure 15-24 compares the MO energies of ethylene with those of butadiene to show that the HOMO and LUMO of butadiene are closer in energy than those of ethylene. The HOMO of butadiene is higher in energy than the HOMO of ethylene, and the LUMO of butadiene is lower in energy than the LUMO of ethylene. Both differences reduce the relative energy of the π2 –> π3* transition. The resulting absorption is at 217 nm (540 kJ/mol). which can be measured using standard UV spectrometer.
What is the general rule for the effects of conjugation on the wavelength of UV absorption?
We can summarize the effects of conjugation on the wavelength of UV absorption by stating a general rule: A compound that contains a longer chain of conjugated double bonds absorbs light at a longer wavelength. The trend of longer wavelengths for longer conjugated chains continues, and at seven conjugated double bonds, the absorption surpasses 400 nm and enters in the visible portion of the spectrum.
Do isolated double bonds contribute to UV absorption?
Because they have no interaction with each other, isolated double bonds do not contribute to shifting the UV absorption to longer wavelengths. Both their reactions and their UV absorptions are like those of simple alkenes. For example, penta-1,4-diene absorbs at 178 nm, a value that is typical of simple alkenes rather than conjugated dienes.
How does light travel through UV-visible spectroscopy system?
The spectrometer (Figure 15-26) has a source that emits all frequencies of UV light (above 200 nm). This light passes through a monochromator, which uses a diffraction grating or a prism to spread the light into a spectrum and select one wavelength. This single wavelength of light is split into two beams, with one beam passing through the sample cell and the other passing through the reference (solvent) cell. The detector continously measures the intensity ratio of the reference beam (Ir) compared with sample beam (Is). As the sepctrometer scans the wavelengths in the UV region, a printer draws a graph (called the spectrum) of the absorbance of the sample as a function of the wavelength.
Describe the UV spectrum of isoprene
The UV spectrum of isoprene (2-methylbuta-1,3-diene) is shown in Figure 15-27. This spectrum could be summarized as follows:
λmax = 222 nm ε = 20,000
The value of λmax is read directly from the spectrum, but the molar absorptivity ε must be calculated from the concentration of the solution and the path length of the cell. For an isoprene concentration of 4 x 10-5 M and a 1-cm cell, the molar absorptivity is found by rearranging Beer’s Law ( A = εcL )
ε = A/cL = .8/(4 x 10-5) = 20,000
What are the absorption maxima of the common types of systems?
Rank the following dienes in order of increasing values λmax. (Their actual absorption maxima are 185 nm, 235 nm, 273 nm, and 300 nm)
Using the examples in Table 15-2 to guide you, match foud of the follwing UV absorption maxima (λmax) with the corresponding compounds:
- 232 nm
- 256 nm
- 273 nm
- 292 nm
- 313 nm
- 353 nm
Do objects have their own light source?
Colored objects do not emit their own light. They reflect part of the ambient light that falls on them. A white object reflects all of the light, but a colored object absorbs some wavelengths and reflects the rest of the spectrum. The color that we see is what is reflected, that is, the complete spectrum minus the portion that is absorbed. Therefore, we observe the opposite, or complement, of the light that is absorbed. For example, ß-carotene, the orange color in carrots, has 11 conjugated double bonds. It absorbs strongly at 454 nm, in the blue portion of the spectrum, reflecting the orange complement.
Define:
Dyes
Dyes are intensely colored compounds used in fabrics, plastics, inks, and other products. Dyes were originally extracted from plants or animals and used to color cloth. For example, red carmine (page 2) was extracted from cochineal insects, and blue indigo (the dye used in blue jeans) was extracted from plant material. Both of these dyes are now synthesized in large quantities. The Romans extracted the indigo derivative Tyrian purple (imperial purple) from a sea snail and used the dye to color the robes of emperors and high-ranking senators.
What role have industrial chemist played in the development of dyes?
Industrial chemists have developed thousands of commercial dyes for every imaginable use, such as fabrics, hair color, inks, toys, and foods. Many dyes are toxic, so the US government has regulated their use in foods since 1906, when the Pure Food and Drug Act created a group of dyes that were approved for coloring foods. Like all unnecessary food additives, food dyes have come under intense scrutiny to determine which ones are safest, and whether any of them cause significant side effects. Only seven dyes are currently approved for unrestricted food use in the US. Two of these food dyes are Indigo Carmine and Sunset Yellow shown below.
Phenolphthalein is an acid–base indicator that is colorless below pH 8 and red above pH 8. Explain briefly why the first structure is colorless and the second structure is colored.
List the most common ring systems in biomolecules.
What role do amino acids play in UV-visible spectroscopy?
Proteins are polymers of twenty common amino acids (Chapter 24), plus occasional rare amino acids. Four of the twenty common amino acids contain conjugated ring systems that strongly absorb UV light, making almost all proteins detectable and quantifiable by UV analysis. The four common UV-absorbing amino acids (shown below) are phenylalanine, tyrosine, histidine, and tryptophan. The standard wavelength for measuring protein absorbance is 280 nm, where most of the absorption is due to tryptophan and tyrosine, with a small contribution from phenylalanine.
What is the role of UV-visible spectroscopy in alkaline phosphatase?
Alkaline Phosphatase removes the phosphate group from many types of biomolecules. Abnormal levels of alkaline phosphatase can indicate liver and bone disorders, among other conditions. Alkaline phosphatase gives a UV spectrum similar to other proteins, so other proteins would interfere with a direct analysis, but we can measure its distinctive ability to remove phosphate groups. We add the colorless compound indoxyl phosphate, which loses its phosphate group when it reacts with the alkaline phosphatase enzyme. The product is indoxyl, which quickly dimerizes to blue indigo. By setting up the UV–visible spectrometer to measure the amount of indigo produced in a certain time period, we can calculate the amount of alkaline phosphatase present in the blood.
