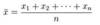Exam 2 Flashcards
What are dependent variables and what are examples?
The outcome variable measured
May be changed or influenced by manipulation of the independent variable
What are conceptual defined dependent variables?
Conceptual variable - the general idea of what needs to be measured in a study: i.e. strength
Must be defined in specific measurable terms for use in the study (once defined, becomes the operational variable)
What are the levels of precision of measurement and what are examples?
The level of measurement/precision of the dependent variable is one factor that determines the choice of statistical tests that can be used to analyze the data
- Nominal (Count Data)
- Ordinal (Rank Order)
- Interval
- Ratio
What is reliability and why is it important?
Reliability: An instrument or test is said to be reliable if it yields consistent results when repeated measurements are taken
3 Forms of Reliability:
- Intra-rater reliability
- Inter-rater reliability
- Parallel-forms reliability
All three forms require comparisons of two or more measures taken from the same set of subjects
Requires a statistical measure of this comparison – correlation
Results of these statistical tests are 0 to 1, with 1 being a perfect correlation and 0 being no correlation
For a reliable comparison the association must be as close to 1 as possible and at least > 0.8
What is validity and why is it important?
Validity - the measure or instrument (measuring tool) is described as being valid when it measures what it is supposed to measure
A measure/instrument cannot be considered universally valid.
- Validity is relative to the purpose of testing
- Validity is relative to the subjects tested
Validity is a matter of degree; instruments or tests are described by how valid they are, not whether they are valid or not
Validity assessments can be made by judgment (judgmental validity) or by measurements (empirical validity)
Judgmental Validity
Based upon professional judgment of the appropriateness of a measurement or instrument
2 principle forms:
- Face validity
- Content validity
What are Sensitivity, Specificity and Predictive Values?
Clinical research often investigates the statistical relationship between symptoms (or test results) and the presence of disease
There are 4 measures of this relationship:
- Sensitivity
- Specificity
- Positive Predictive Values
- Negative Predictive Values
What are extraneous/confounding variables and what are examples?
Confounding or Extraneous Variables: Biasing variables – produce differences between groups other than the independent variables
These variables interfere with assessment of the effects of the independent variable because they, in addition to the independent variable, potentially affect the dependent variable
Analysis of the Dependent Variable
A single research study may have many dependent variables
Most analyses only consider one dependent variable at a time
Univariate Analyses- each dependent variable analysis is considered a separate study for the purposes of statistical analysis
What are operationally defined dependent variables and what are examples?
The specific, measurable form of the conceptual variable
The same conceptual variable could be measured many different ways; defined in each study
i.e: to define strength = Maximum amount of weight (in kilograms) that could be lifted 1 time (1 rep max)
Nominal Level of Precision
Score for each subject is placed into one of two or more, mutually exclusive categories
Most commonly, nominal data are frequencies or counts of the number of subjects or measurements which fall into each category.
Also termed discontinuous data because each category is discrete and there is no continuity between categories
There is also no implied order in these categories
Examples:
- Color of cars in parking lot
- Gender of subjects
- Stutter – yes/no
Can only indicate equal (=) or not equal (≠)
Ordinal Level of Precision
Score is a discrete measure or category (discontinuous) but there is a distinct and agreed upon order of these measures, categories
The order is symbolized with the use of numbers, but there is no implication of equal intervals between the numbers
Examples include any ordered scale
Can say = & ≠, and greater than (>) or less than (<)
Interval Level of Precision
Numbers in an agreed upon order and there are equal intervals between the numbers
Continuous data ordered in a logical sequence with equal intervals between all of the numbers and intervening numbers have a meaningful value
There is no true beginning value – there is a 0 but it is an arbitrary point
Examples:
- Temperature
- Dates
- Latitude (from +90° to −90° with equator being 0
Interval level can say = or ≠; < or >; and how much higher (+) or how much lower (−)
(Interval does not have a true 0 value; Ratio does)
Ratio Level of Precision
Numbers in an agreed upon order and there are equal intervals between the numbers
Continuous data ordered in a logical sequence with equal intervals between all of the numbers and intervening numbers have a meaningful value
There is a true beginning value – a true 0 value
Ratio level – can do everything with interval but also can us terms like 2X or double (×) or half (÷) when comparing values
(Interval does not have a true 0 value; Ratio does)
Mathematical Comparison of Precision Levels
Nominal level – can only indicate equal (=) or not equal (≠)
Ordinal level – can say not only = & ≠ but also greater than (>) or less than (< or >; and how much higher (+) or how much lower (−)
Interval level can say = or ≠; < or >; and how much higher (+) or how much lower (−)
Ratio level – can do everything with interval but also can us terms like 2X or double (×) or half (÷) when comparing values
Statistical Reasoning for the Precision Levels
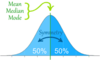
Nominal level – unit of central tendency is the mode and any variability is assessed using range of values
Ordinal level – unit of central tendency is the median and any variability is assessed using range of values
Interval or Ratio (Metric) - unit of central tendency is the mean and any variability is assessed using standard deviation if normally distributed
Intra-Rater Reliability
Tested by having a group of subjects tested and then re-tested by the same person and/or instrument after an appropriate period of time
Inter-Rater Reliability
Reliability between measurements taken by two or more investigators or instruments
Different instruments or different investigators
Objective Testing
Usually has both high intra-rater and inter-rater reliabilities
Example: isokinetic dynamometer to measure muscle force (torque)
Raters are trained in the use and calibration of the instrument
Parallel Forms Reliability
Specific type of reliability used when the initial testing itself may affect the second testing.
Two separate forms of the exam covering the same material, or testing the same characteristic, are used
Investigators must first do testing to demonstrate that the two forms of the test are, in fact, equivalent
Face Validity (Judgmental)
Judgment of whether an instrument appears to be valid on the face of it - on superficial inspection, does it appear to measure what it purports to measure?
To accurately assess this requires a good deal of knowledge about the instrument and what it is to measure.
That is why professional judgment is emphasized in the definition of judgmental validity
Content Validity (Judgmental)
Judgment on the appropriateness of its contents.
The overall instrument and parts of the instrument are reviewed by experts to determine that the content of the instrument matches what the instrument is designed to measure
Empirical Validity (Criterion-Related Validity)
Use of data, or evidence, to see if a measure (operational definition) yields scores that agree with a direct measure of performance
2 forms of Empirical Validity:
- Predictive
- Concurrent
Predictive Validity (Empirical)
Measures to what extent the instrument predicts an outcome variable.
Concurrent Validity (Empirical)
Measures the extent to which the measures taken by the instrument correspond to a known Gold Standard
Correlation statistics are also used to measure the validity
Inter-Relationship between Reliability and Validity
For an instrument or test to be useful it must be both valid and reliable
Sensitivity
Formula: Sensitivity = TP/TP+FN
Definition: the probability that a symptom is present (or screening test is positive) given that the person does have the disease
Patient Relevance*: “I know my patient has the disease. What is the chance that the test will show that my patient has it?”
Specificity
Formula: Specificity = TN/TN+FP
Definition: the probability that a symptom is not present (or screening test is negative) given that the person does not have the disease
Patient Relevance: “I know my patient doesn’t have the disease. What is the chance that the test will show that my patient doesn’t have it?”
Positive Predictive Value
Formula: TP/TP+FP
Definition: the probability that a person has the disease given a positive test result
Patient Relevance: “I just got a positive test result back on my patient. What is the chance that my patient actually has the disease?”
Negative Predictive Value
Formula: TN/TN+FN
Definition: the probability that a person does not have the disease given a negative test
Patient Relevance: “I just got a negative test result back on my patient. What is the chance that my patient actually doesn’t have the disease?”
What is the definition and use of descriptive statistics?
Statistics used to characterize shape, distribution, central tendency & variation (variability) of a population or sample
What is the parameter & what is the statistic?
Parameter –is the individual value or data point
Statistic – calculated descriptive index
What are measures of central tendency?
•Distributions described as the variation pattern around the point of central tendency
Measures of central tendency:
- Mean – the arithmetic mean which is the sum of all values in the distribution divided by the number of values
- Median – the middle value in a distribution of values; half way in number from the lowest to highest numbers
- Mode – value in the distribution with the highest frequency – most common number in the distribution
What is and what measures are there of score distribution and frequency distribution?
Frequency distribution – rank order of how many times a particular value occurred
Can be displayed as percentage value and cumulative percentage
Data can be grouped into classes or ranks
Histogram
Representation of tabulated frequencies, shown as adjacent rectangles, in discrete intervals, with height equal to the frequency of the observations in the interval
Frequency Polygon
Intervals represented as points and level on vertical axis represents the frequency of the observations in the interval
Normal Distribution
Variation of the distribution pattern around the point of central tendency:
Symmetric distribution of values of around the point of central tendency
Mode, median & mean all the same point
Skewed Distribution
Asymmetric distribution of values of around the point of central tendency
Described as positive or negative skew based upon where majority of values are compared to the mode
Use “tail” of distribution to determine skew
Median & mean deviate from the mode in skewed distributions
Mean is most sensitive to skew
Therefore mean should be used ONLY in normal distributions as a measure of central tendency
Quantification of Variation of the Distribution Pattern: Range
Highest to lowest value of the distribution – 58 to 75 in illustration
No measure of how much each value deviates from point of central tendency
Quantification of Variability: Variance
Assess deviation of each score from the mean – deviation score
Sum of these deviation scores = 0 so take sum of deviation scores squared – called the sum of squares (SS)
Divide the SS by the number of scores (n) to get the SAMPLE VARIANCE also called mean square (MS)
Better estimation of the POPULATION VARIANCE is to divide the sum of squares by n-1
Quartiles
Quartiles of a ranked data set are the three points that divide the data set into four equal groups - 25th percentile, 50th percentile & 75th percentile
Each group comprises a quarter of the entire data set
Different Quartiles:
- Lower (bottom) quartile – < 25th%
- Lower middle quartile − 25th% − 50th%
- Upper middle quartile − 50th% − 75th%
- Upper (top) quartile − > 75th%
Interquartile range is from 25th% − 75th%
Graphic Display of Mean/SD
Common display in graphs of mean as a point and an error bar showing one SD around that mean
Allows for easy comparison between groups
Graphic Display of Median, Quartiles & Range (estimate)
Box & Whisker Plot:
- Line at center of box - Median
- Box - Interquartile range (IQR)
- Whiskers (bars) - 1.5 x IQR – approximates range
Box & Whisker plots allow for easy comparison between groups when using median, quartiles and ranges
What does probability mean in terms of an individual or population?
Applied to Groups of Data
The greater the deviation from mean the greater the probability of NOT being in the group
Critical when comparing two groups – what is the probability of 2 groups being from different populations
- 68% of all values are within 1 SD of mean
- 95% of all values are within 2 SD of mean
- 99% of all values are within 3 SD of mean
- > deviation from mean less probability of being in the group
Probability of Pair of Dice Toss
value of 2 - 1/36 – p=.028
- value of 3 – 2/36 – p=.056
- value of 4 – 3/36 - p=.083
- value of 5 – 4/36 - p=.111
- value of 6 – 5/36 - p=.139
- value of 7 – 6/36 - p=.167
- value of 8 – 5/36 - p=.139
- value of 9 – 4/36 - p=.111
- value of 10 – 3/36 - p=.083
- value of 11 – 2/37 – p=.056
- value of 12 – 1/36 - p=.028
Distributions of Outcome Measure
Applied to Groups of Data
Distributions of outcome measure before (blue) & after (red) an intervention
What probability that the intervention produced a change in the outcome?
What probability that the difference between these two distributions is due to chance alone and not the result of the intervention?
Experimental Errors
Reject or not reject the experimental or null hypothesis – 4 possible outcomes
Correctly reject null hypothesis – experimental hypothesis is true
Correctly reject experimental hypothesis – null hypothesis is true
Incorrectly reject null hypothesis – null hypothesis is true, called Type I error
Incorrectly reject experimental hypothesis – experimental hypothesis is true – Type II Error
Effect size
Factor that assesses true difference between groups
If means of 2 groups very different but groups have a high variability – there may not really be a difference between the 2 groups
If there is small difference between the means of two groups, but each group is very homogeneous, then could have a true difference between the groups
Effect size involves variability within groups & mean difference between groups
Effect size equals difference between means of two groups divided by the pooled standard deviation
Cohen states that ES < 0.2 is small, around 0.5 is medium & > 0.8 is large
Power Analysis is done before the study (a priori) to determine the needed sample sizes
What is the basis for the statistical analysis of the two-group difference?
Ratio of between groups to within groups–Between groups difference has both treatment effect + experimental error
Within groups variability due sole to experimental error
- So if no treatment effect the ratio is 1
Desired outcome is a >> a number as possible when treatment effect >>>> experimental error
Think of it like a signal to noise ratio – lot of signal compared to noise wanted
