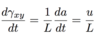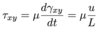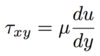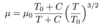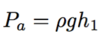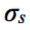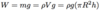Fluid Mechanics Flashcards
(299 cards)
1
Q
A solid is matter that…
A
retains it’s shape (lump of metal)
2
Q
A liquid is matter that…
A
deforms to the shape of its container and forms a free surface (glass of water, cup of tea, ocean, etc)
3
Q
A gas is matter that…
A
occupies the full extent of its container (i.e. air in a balloon etc.)
4
Q
A fluid is a substance which is…
A
either a liquid or a gas
5
Q
A fluid is a matter that deforms continuously under the action of…
A
Shear stress
6
Q
Define a system
A
A quantity of matter or region of space chosen for study
7
Q
What resides outside the system?
A
The surroundings
8
Q
The system is enclosed by its ____?
A
Boundaries
9
Q
Define real and solid boundaries
A
Real: Solid boundaries
Imaginary: Notional surfaces that define a control volume
10
Q
A system can be…(3 things)
A
Open, close or isolated
11
Q
What is not allowed and what is allowed to cross the boundaries in a closed system?
A
- Mass is not because mass is fixed
- Energy is
12
Q
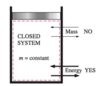
Boundaries are permitted to ____ in a closed system?
A
Move
13
Q
What is allowed to cross in an open system?
A
Mass and energy
14
Q
What can cross boundaries in an isolated system?
A
No mass or energy can cross the boundaries
15
Q
Properties can either be…(2 things)
A
Intensive or extensive
16
Q
Define intesive properties
A
Intensive properties are independent of the size of the system
17
Q
Define Extensive properties
A
Extensive properties are dependent on the extent of the system
18
Q
Give two examples of inentisive properties of a system and why
A
Pressure and temperature - they are independent of the size of the system
19
Q
Give two example of extensive properties of a system and why
A
Mass and volume - they are dependent of the size of the system
20
Q
Define density and it’s equation and units
A
The mass per unit volume of a substance
21
Q
Define specific volume of a substance
A
- Specific volume defined as how much volume holds 1 kg of fluid mass
- The specific volume is the reciprocal of the density, i.e.
22
Q
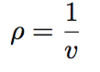
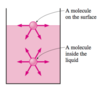
Define Continuum fluid
A
Homogeneous, continuous matter with no gaps
23
Q
When is the assumption of continuum okay?
A
When the size of the system is large with respect to the spacing between molecules
24
Q
What is the collision and rebound amongst molecules in the system represented by in the continuum?
A
Thermodynamic pressure, p (M/m2)
25
What is it called when the continuum assumption cal no longer hold and individual particles should be considered?
**Rarified gas flow theory**
26
Define **viscosity**
Internal resistance of fluid to motion
27
As fluid passes over a solid object, the interaction with the solid causes a ____ \_\_\_\_to form in the region near to the solid
As fluid passes over a solid object, the interaction with the solid causes a **_boundary layer_** to form in the region near to the solid
28
Define **inviscid** and **viscous** flows
* **Inviscid** flows are idealised and have zero viscosity
* All real flows are **viscous**
29
Define **Internal** and **external** flows
* **Internal** flows have an inlet and outlet (i.e. a pipe)
* **External** flows are unbounded (flow around an aeroplane)
30
Define **Steady** and **unsteady** flows
* **Steady** flows do not change with time
* **Unsteady** flows are time dependent
31
Define **laminar** and **turbulent** flows
* In **laminar** flows, fluid layers pass over each other smoothly
* **Turbulent** flows are chaotic and seemingly random
32
Define **compressible** and **incompressible** flows
* For **compressible** flows, density can change significantly and can affect the flow
* In **incompressible** flows, density is a constant
33
# Define
1. **One**-**dimensional**
2. **Two**-**dimensional**
3. **Three**-**dimensional** flows
1. All flows are **three**-**dimensional** to some degree
2. We can approximate if the flow does not vary significantly in certain dimensions
3. The flow through a nozzle accelerates mainly along the nozzle - can be treated as a **one**-**dimensional** flow
34
What is the *equation* and *symbol* for **Normal stress**
35
What is the *equation* and *symbol* for **axial** **strain**
36
Equation for **Young's Modulus of Elasticity**
37
In a control volume, the pressure inside the volume is ____ \_\_\_\_ as the external pressure
In a control volume, the pressure inside the volume is **_the same_** as the external pressure
38
Equation for change in pressure
39
Equation of the Modulus of elasticity
40
K = ?
and because
þ = 1/v
K = ?
K = -v(dp/dv)
and because
þ = 1/v
K = þ(dp/dþ)
41
Shear strain equation and symbol
42
Shear stress equation and symbol
43
G is the...?
Shear modulus
44
In solids, the shear stress is ____ to the ____ \_\_\_\_
In solids, the shear stress is **_proportional**_ to the _**shear_ _strain_**
45
In fluids, viscous stress is ____ to the ____ of \_\_\_\_
In fluids, **_viscous_** stress is proportional to the *rate* of **_strain_**
46
When *shear stress,* Jxy(backwards J), acts on a fluid element, the deformation *rate* is...(define u)
da/dt = u
**u** is the **upper** **surface** **fluid** **velocity**
47
Equation for the ***shear strain rate***
48
Equation given that **vicous stress** is **proportional** to the **rate of strain** and in the limit of L tending to zero
**Vicous stress** is **proportional** to the **rate of strain**
(Picture)
Limit of L tending to zero
limL→0Jxy(backwards) = u(du/dy)
49
In this equation;
what is the constant of proportionality,
what is it,
and what is it's units
u
The dynamic viscosity
kg/ms
50
Define a Newtonian Fluid
A Newtonian fluid is defined as a fluid in which the dynamic viscosity is independent of du/dy
51
In a *Newtonian fluid,* the ____ is dependent on the shear rate
In a *Newtonian fluid,* the **_viscosity_** is dependent on the **shear rate**
52
* Dilatant or shear thickening fluid
* Viscosity ____ with shear rate
* Pseudoplastic or shear thinning fluids
* Viscosity ____ with shear rate
* Dilatant or shear thickening fluid -
* **Viscosity _increases_ with shear rate**
* Pseudoplastic or shear thinning fluids
* **V****iscosity _decreases_ with shear rate**
53
The **viscosity** of a fluid varies with...?
Temperature
54
What's it called to determine the value of viscosity for a gas and what is the equation?
**Sutherland's Law**
55
This is Sutherland's law used to determine the value of viscosity for a gas.
Define each symbol and it's values
* μ0 =reference viscosity (kg/ms) at reference temperature T0
* T = input temperature (K)
* T0 = reference temperature (K)
* C = Sutherland’s constant for material in question
* For air,
* C = 110.56K
* T0 = 273.11K
* μ0 = 1.7894x10-5kg/ms
56
The viscosity of a gas ____ with temperature
The viscosity of a gas **_increases_** with temperature
57
Equation used determine the value of viscosity for liquids?
* For water,
* a =2.414x10-5 kg/ms,
* b = 247.8K,
* c = 140K
58
The viscosity of a liquid ____ with temperature
**_decreases_**
59
# Define **Kinematic viscosity**
**Kinematic** **viscosity** is defined as the **ratio of dynamic viscosity to density**
60
What are the equation and units for Kinematic viscosity
m2/s
61
What is often used in an **incompressible** **flow** and why?
**Kinematic** **viscosity** is as **density** is **constant** in an **incompressible** **flow**
62
If the radius of the shaft, R, is much greater than the spacing l then...
63
On rotation in radians is...
2π radians
64
Angular velocity is...? (equation)
Where n dot is the number of rotations per unit time
65
What is **pressure** and the **units** for it?
Pressure is the force per unit area exerted by the fluid on the container
**Pascals** (N/m2)
66
1 bar = ?
1 atm = ?
1 psi = ?
You don't have to remember these it's just good too
67
Define **Absolute pressure *P*abs**
The pressure at a point relative to absolute vacuum (i.e. zero pressure)
68
Define **Atmospheric pressure** *Patm*
The atmospheric pressure at a point
69
Most pressure-measuring devices are calibrated to read ____ at atmospheric pressure
Zero
70
What is the difference called between absolute pressure and atmospheric pressure?
Gauge pressure, *Pgauge*
71
Pabs = ? (Two equations)
Pabs = Patm + Pgauge
Pabs = Patm - Pvac
72
What are pressures below atmospheric pressures called?
Vacuum pressure, Pvac
73
Pressure is infact a...?
Scalar - it has a magnitude but no specific volume
74
The pressure at a point in a fluid has the ____ \_\_\_\_ in all directions
The pressure at a point in a fluid has the **_same_ _magnitude_** in all directions
75
P2 = ? (Manometer)
76
Pressure increases ____ with depth in a fluid
Linearly
77
Change in *z* or *h* are commonly referred to as...?
**Pressure head**
78
Why are all pressures the same here even though the weight of the water is different?
Because they are all the same height
79
What is **Pascal's Principle?**
**Pascal’s Principle:**
* *The pressure applied to a confined fluid increases the pressure throughout by the same amount*
In an incompressible fluid this change is instantaneous
80
In an incompressible fluid when the Patm changes the pressure everywhere else in the fluid will change...
Instantaneous
81
F2/F1 = ?
F2/F1 = A2/A1
82
P2 = ?
Change in P = ? (Two equations)
83
* Pressure at point 1 must ____ the pressure at point 2
* The column of fluid with height *h* indicates that P2 is ____ than P1
* Pressure at point 1 must **_equal_** the pressure at point 2
* The column of fluid with height *h* indicates that P2 is **_greater_** than P1
84
The use of a manometer is based on the assumption that...
The use of a manometer is based on the assumption that the density of the manometer fluid is much higher than that of the fluid in the reservoirs
85
In an inclined manometer, P1 = ?
86
How do you use a Column Barometer and what are they commonly used for?
* Barometers are commonly used to measure ambient pressure
* Fill a tube up completely with the working fluid
* Place it upside down in an open vessel of the working fluid
* The top chamber is essenDally a vacuum
* The height of the column of working fluid above the top of the open vessel gives the ambient pressure
87
Equation for ambient pressure, Pa
88
1atm of mercury = ?
1atm = 760mmHg = 101,325Pa
89
What is **meniscus**?
When there is a bend in water - it is never quite flat
90
Does a liquid have surface tension?
Give an example.
Yes, pond skaters for example
91
What is the symbol for surface tension and units?
N/m
92
Define the **Capillary effect**
When surface tension affects fluid in small-diameter tubes
93
Define concave and convex meniscus
94
What is the equation for the weight of the fluid of the column?
95
Define the contact angle, Ø
The angle that the tangent of the liquid surface makes with the solid surface at the point of contact
96
For wetting liquids, Ø ? 90°
So the rise is...?
Ø \< 90°
So the rise is **positive**
97
For non-wetting liquids, Ø ? 90°
So the rise is...?
Ø \> 90°
So the rise is **negative**
98
Capillary effect is normally negligible for tubes of diameter ____ than 1 cm
Capillary effect is normally negligible for tubes of diameter **_greater_** than 1 cm
99
How do we minimise errors in manometry from the capillary effect?
* Use sufficiently wide tubes
* More dense liquids are less affected by capillary rise
100
Manometry is a branch of...?
**Hydrostatics**
101
Summarise the principles of **hydrostatics**
1. There are no shearing forces within a body of static fluids
2. Pressure is perpendicular to the surface on which it acts
3. Pressure at any point in a fluid at rest is the same in all directions
4. Pressure increases linearly with depth in a static fluid
5. Pressure is proportional to the density of the fluid
6. Pressure is the same at all points in the same horizontal plane in a fluid at rest
7. External pressure applied at any point to an enclosed fluid is transmitted unchanged throughout the fluid (for an incompressible fluid this transmission is instantaneous)
102
Fluid statics is the study of...
Hydrostatics it the study of...
Aerostatics is the study of...
...fluids at rest
...liquids at rest
...gases at rest
103
Define centroid
The centre of the body
104
Force = ?
Pressure x Area
105
The pressure at the centroid of the surface, *Pc*, is the same as...?
...the average pressure acting on the surface
106
FR = ?
FR = PaveA
107
Pave = ?
Pave = P0 + þghc
108
hc is the...?
...vertical distance of the centroid from the liquid free surface
109
The resultant force does not act on the \_\_\_\_, it acts at the ____ \_\_ \_\_\_\_
The resultant force does not act on the **_centroid_**, it acts at the **_centre_** **_of_** **_pressure_**
110
Equation for second moment of area about the x-axis
111
The moment from the pressure distribution must equal the moment from...?
...the resultant force
112
What is a pressure prism?
When,
* Area is the area of the base plate
* Height is the pressure distribution
113
???
114
Finding the hydrostastic force reduces to finding the...?
...volume of the prism and the position of its centroid
115
For a rectangular plate, the second moment of area passing through the centroid is given by...? (Equation)
116
yc =?
yc = s + b/2
117
If the plate is **vertical**, sinØ = ?
1
118
If the plate is **horizontal**, there is a...?
...uniform pressure distribution across the plate
119
For forces on a curved surface, how do we calculate the magnitude acting on the curved surface?
* Horizontal force - FH
* Vertical force - FV
The magnitude of the resultant force acting on the curved surface is... (picture)
120
If
* Horizontal force - FH
* Vertical force - FV
What is the equation for the force makes an angle with the horizontal?
121
FB = ÞfgV which is...?
...the weight of the liquid of the same volume as the body
122
What is **Archimedes**' **Principle**?
The buoyant force acting on a body immersed in a fluid is equal to the weight of the fluid displaced by the body, and it acts upwards through the centroid of the displaced volume
123
Why do some bodies float and other bodies sink?
1. **Less dense** than the surrounding fluid =
2. **Same density** as the surrounding fluid =
3. **More dense** than the surrounding fluid =
1. **Less dense** than the surrounding fluid **_will_** **_float_**
2. **Same density** as the surrounding fluid are **_neutrally_ _buoyant_**
3. **More dense** than the surrounding fluid **_will_** **_sink_**
124
How do we define the stability of a system?
1. A small disturbance applied to the ball in (1) results in the ball returning to its original position - the system is **stable**
2. A small disturbance applied to the ball in (2) results in the ball moving, but not running off or returning to its original place - the system is **neutrally** **stable**
3. A small disturbance applied to the ball in (3) results in the ball rolling away and never returning to its original posiFon - the system is **unstable**
125
Rotational stability depends on the locations of...
...the centre of gravity, *G*, and the centre of buoyancy, *B*
126
If the centre of gravity is ____ the centre of ____ = ?
If it is top heavy = ?
If the centre of gravity is **_below_** the centre of **_buoyancy_** = **More stable**
If it is top heavy = bad
127
An object in which the **centre of gravity** and **centre of buoyancy** **coincide** is...?
...**neutrally stable**
128
How can a floating body can be stable even if the centre of gravity is above the centre of buoyancy?
* A **disturbance** causes the floating body to rotate
* The centre of buoyancy moves as the shape of the submerged body changes
* B’ is the **new** centre of buoyancy, and B’ and G act to create a **restoring** **moment**
129
What is the distance *GM*?
And the **larger** it is...?
Distance *GM* is the metacentric height - the **larger** it is, the **more** **stable** the **floating body**
130
Visulsation techniques that are commonly used include...(4 things)
- Smoke/Dye visualisation
- Schlieren and shadowgraph imagery
- Laser Induced Fluorescence
- Particle Image Velocimetry
(Don't worry too much about this though)
131
What is the smoke/Dye visulisation method?
1. Inject smoke into air flow, or dye into a liquid flow
2. The injected material acts as a marker in the flow
132
Who was the first person to use the visulaisation technique?
Osborne Reynolds
133
What is now known as the **Reynolds number**?
**Reynolds number** is to recognise the **dependence** of the **state of the flow** on certain parameters
134
With an increasing Re, what happens to flows?
135
Reynolds number is a....?
...dimensionless number
136
Re = ?
137
Re = ? For an *incrompressible flow*
138
Define each symbol in these equations
* ρ is the fluid density
* V is an appropriate velocity scale in the flow
* L is an appropriate length scale in the flow
* Choice between V and L is arbitory, be careful with them
* μ is the dynamic viscosity of the fluid
* ν is the kinematic viscosity of the fluid
139
What would it look like when Re = 3000?
140
What would Re = 16,500 look like?
141
**Schlieren** **imagery** requires a...
...change in refractive index in the medium
142
How does Schileren Imagery work?
* Light source is collimated by a mirror and passed through the field of interest
* A second mirror refocuses the light, re- imaging the point where it is intercepted by an adjustable knife edge
* The knife edge removes bent rays of light
143
How does the Planar Laser Induced Fluorescence work?
* This visualisation technique uses a laser sheet to illuminate the fluid
* The fluid contains a fluorescent substance
* The laser sheet excites electrons in the medium, which then emit light waves as the electrons return to their ground state
* This technique is commonly used to investigate chemical reactions and mixing in turbulent flows
144
How does **Particle Image Velocimetry** work?
* In PIV a Laser sheet is used to illuminate the fluid
* The fluid is seeded with small particles which can be tracked by taking
* repeated photographs of the flow
* Velocity information can be obtained by tracking the particles in the flow
* This technique is a non-intrusive method of obtaining velocity information from a flow
145
Define **streamline**
A **streamline** is a curve whose tangent at any point is in the direction of the velocity vector at that point
146
Define **streakline**
A **streakline** is the path formed by the release of a series of particles at different times from a fixed location in the flow
147
Define **pathline**
A **pathline** is the path formed by one fluid particle as it moves in the flow
148
In a **steady** flow...
...**streamlines**, **streaklines**, and **pathlines** are **equivalent**
149
Can fluid cross a streamline?
Why?
*No fluid can cross a streamline* as the tangent of the streamline is the velocity vector at any point
150
The 3-D extension of a streamline is called a...?
...**streamtube**
All fluid entering a streamtube at one end must exit it at the other end
151
Total change of velocity = ?
Difference of velocity between points at the given instant + change of velocity occurring at the target point in time δt
152
For fluid particle motion, v = ?
v = ds/dt
153
Fluid problems can be treated in...
**Lagrangian** or **Eulerian** frames of reference
154
What is **Lagrangian** frame of reference?
* Apply physical principles to fluid particles
* Frame of reference moves along with the particles
155
What is Eulerian frames of reference
* Apply physical principles to a control volume
* Control volume is fixed in space - flow travels through it
156
Mass flowing per unit time = ?
Rate of increase of momentum from AB to CD = ?
Pressure force in direction of motion = ?
Pressure force opposing motion = ?
Side pressure force producing a component in direction of motion = ?
Gravitational force opposing motion = ?
Resultant force in direction of motion = ?
Weight of fluid element Angle = ?
157
Pressure always acts...?
Inwards
158
What is **Bernoulli's Equation?**
159
Try to remember the other 3 Bernoulli equations when you intergrate
160
To what is Bernoulli’s equation limited?
The flow must be...(5 things)
1. Steady: du/dt =0
2. Frictionless: μ =0
3. No work or heat transfer to system
4. Incompressible: ρ = constant
5. Irrotational - no vorticity
161
162
Bernoulli's equation states the conversation of...
...**total pressure**
163
Define **stagnation pressure**
The **stagnation** **pressure** is the **sum** of the **static** and the **dynamic** **pressures**
164
What is the equation for **stagnation pressure**?
165
In a horizontal flow, or in an air flow of velocity greater than 5 m/s, changes in ρgz are \_\_\_\_, and stagnation pressure is \_\_\_\_
**_negligible_****,** and stagnation pressure is **_constant_**
166
For aerodynamic applications, the Bernoulli equation simplifies to...?
167
What device uses different pressures to measure the velocity in a flow?
A **Pitot Tube**
168
What are the dimensions of this equation and what do the seperate parts respresent?
* The dimensions of this equation are of L
* p/ρg = pressure head
* v2/2g = velocity head
* z = elevation head
* H = total head - the height to which fluid rises in a pitot tube open to the atmosphere
169
What is Einstein's theory of Special Relativity?
*E = mc2*
170
Mass cannot be ____ \_\_ ____ in a fluid flow with no ____ reactions
Mass cannot be created or destroyed with no nuclear reactions
171
Mass of fluid entering the system per unit time = ?
Mass of fluid entering the system per unit time =
**Mass of fluid leaving per unit time** + **increase of mass in the control volume per unit time**
172
Define this symbol and its units
Mass flow rate (kg/s)
173
For a steady flow, the mass inside the control volume is...?
...**constant**
174
Mass of fluid entering the system per unit time = ?
= Mass of fluid leaving per unit time
175
What is the continuity equation?
176
For an **incompressible** **flow**, the ____ is **constant**, so the **continuity equation** is...?
For an **incompressible** **flow,** the **_density_** is constant so the **continuity equation** is...
177
What is *Q* in this equation and it's units?
*Q* is the **volumetric** **flow** rate (m3/s)
178
Q1 = ? + ?
So,
A1v1 = ? + ?
Q1 = Q2 + Q3
So,
A1v1 = A2v2 + A3v3
179
180
What **equation** and **device** can be used to **measure** the **velocity** of a flow?
The **continuity equation** and a **venturi flow meter**
181
Simplier continuity equation ? = ?
Where
? \> ?
A1V1 = A2V2
Where
A1 \> A2
182
The value of *H* can be found from the...?
...Manometer reading
183
Manometer contains a fluid of density...?
ρman
184
The **volumetric flow rate** is Q = ?
Q = A1V1
185
For a **Venturi meter**, the **discharge** **coefficient** typically has a value of...?
0.96
186
Some loss of energy will occur in a real system, so a **coefficient of discharge** has to be introduced
Qactual = ?
Some loss of energy will occur in a real system, so a **coefficient of discharge** has to be introduced
Qactual = CdQtheoretical
187
What is it when you **insert** a **sudden** **contraction** into a **pipe**
An **orifice plate**
188
Define the **vena contracta point**
The point of maximum convergence which occurs slightly downstream of the **orifice plate**
189
Define the **momentum** of a **particle** or **object**
momentum = *mv*
190
If a **fluid stream** undergoes a **change in velocity**, there will also be a...?
...**change in momentum**
191
Newton’s 2nd Law dictates that a force is required to produce a change in momentum, so F = ?
Or F = (mv - mu) / t
192
**Force** and **velocities** are **vector** **quantities**, so they have a...?
...**magnitude** and a **direction**
193
Aplying continuity to the control volume...(equation)
194
Force = Rate of...
Force = Rate of change of momentum
195
Newton’s 3rd Law dictates that the fluid will...
...exert an **equal** and **opposite** reaction force on the **surroundings**
196
What do you do if the fluid is not travelling in a straight line?
Split the flow up into its *x* and *y* components
197
In general, the **total force** F acting on a control volume in a given direction will be made up of three components
Force exerted in the given direction on the fluid in the control volume
1. by any solid body within the control volume, or coinciding with the boundaries of the control volume
2. by body forces such as gravity
3. by the fluid outside the control volume
198
Imagine a jet of fluid impacting on a fixed, symmetrical smooth vane
With no fricton or losses, the tangential velocity of the flow leaving the plate has the...
...same velocity as the initial jet
199
From **continuity**, the **mass flow** **out** of the vane must equal...
...the **mass** **flow** **into** the vane
200
For the impact of a jet on a cup, θ = ?
θ = 0°
201
How do you calculate the **resultant** **force** for a deflection of a jet?
202
Reaction force *R* is equal and opposite to the...?
...resultant force
203
What forces act on this system?
* Pressure from the pipe inlet and outlet
* Gravity
* Forces exerted by the walls of the pipe
204
**Mechanical** **energy** is a form of energy that can be converted to...
...**work** by an **ideal** **turbine**
205
**Mechanical** **energy** is the **su****m** of...
...**flow** **energy** plus **kinetic** **energy** plus **potential** **energy**
206
The mechanical energy per unit mass of a flow is...(equation)
207
The **change in flow state** from point 1 to point 2 produces...?
...**work output**
208
What is the inflow energy per unit mass (J/kg)?
209
What do each seperate part of these equations represent?
210
When is the maximum theoretical work output obtained?
When emech2 = 0
211
The efficiency of the idealised system can be defined as...
212
Turbine efficiency can be defined as...
213
Pump efficiency can be defined as...
214
**Friction** again produces **heat** in the system which...
...**reduces** the **useful** **work** **output**
215
Motor efficiency can be defined as...
216
Generator efficiency can be defined as...
217
What is the **combined** **efficiency** when a **motor** and **pump** are connected together?
218
What is the **combined** **efficiency** when a **turbine** and **generator** are connected together?
219
Define these symbols
220
Each term in the **steady** **flow** **energy** **equation** is a measure of \_\_\_\_, and is a useful means to evaluate ____ \_\_\_\_ in systems
Each term in the steady flow energy equation is a measure of **_distance_**, and is a useful means to evaluate **_head_** **_loss_** in systems
221
With **laminar** **flow**, flow is...
...**ordered**, layers of fluid pass each other **smoothly**
222
With **turbulent** **flow**, flow is
...seemingly **random**, **chaotic**, and **irregular**
223
The transition of a flow is determined by...?
...the **Reynolds** **number**
224
For a pipe flow, the Reynolds number is given by...
* vm is the **mean** **flow** **velocity** (m/s)
* Dh is the **hydraulic** **diameter** of the pipe (m)
225
For a **smooth** **walled** **pipe**, flows of the **same** **Reynolds** **number** will have the **same**...
...**characteristics**, i.e. be in the **same** **flow** **regime**
226
Define the **critical** **Reynolds** **number**
The **critical** **Reynolds** **number** is the value at which the **flow** will become **turbulent**
227
Re \< Recrit = ?
**Laminar** flow
228
Recrit ≤ Re ≤ 4,000 = ?
**Transtional** flow
229
Re \> 4,000 = ?
**Turbulent** flow
230
**Reynolds** **number** for smooth walled pipes is...
231
The **mean velocity**, *vm*, is...
The **mean velocity**, *vm*, is the **velocity** at which an
**idealised**, **inviscid** fluid has the **same** **mass** **flow** **rate**
as the **real** **flow**
232
Mean velocity, *vm *= ?
233
Define the **hydraulic diameter**
The **hydraulic** **diameter** is the diameter of an **equivalent circular pipe**
234
Equation for **Hydraulic diameter**
And does the symbol *p* stand for?
P is the **perimeter** of the **original** **conduit**
235
What does the **no-slip** **condition** do and what does it form?
The **no-slip condition** gives the fluid next to the pipe wall a **zero** **velocity** - this forms a **boundary** **layer**
236
The boundary layer grows until it reaches all parts of the pipe - the flow is then said to be...?
...**fully-developed**
237
The **distance** from the **entrance** to the point where the **boundary layers grow** to the **centreline** is called the...?
...**entrance** **length**, Lh
238
For **laminar** **flow**, Lh/D = ?
239
For **turbulent flow**, Lh/D = ?
240
The **wall** **shear** **stress** is at its **highest** at...?
...the **entrance** of the pipe
241
The value of the **wall shear stress** reaches a **constant** at...?
...the **end** of the **entrance length**, *Lh*
242
What is **Reynolds averaging?**
A **time-averaging procedure** when applied to **turbulent** **flow**
243
Adding **friction** to the **flow** results in a **pressure drop** along the pipe caused by...?
...the **shear stress**
244
If there is **no shear stress**, there is **no pressure drop** and the flow becomes...?
...**idealised**
245
For **fully-developed pipe** flow we know that...(equation)
246
What is ∆PL ?
ΔPL is the **pressure loss** along the pipe due to **viscous** **effects**
247
What is the **Hagen-Poiseuille equation** written in terms of **head loss**?
248
What equation is used to show **head loss** for a **laminar flow**?
249
What is the the **Darcy-Weisbach equation** for a **circular pipe**?
*f* is called the **friction factor**
250
Define the **friction factor**
**Friction factor** is the **ratio** of the **pressure** **drop** to the **dynamic pressure**
251
**Darcy's friction factor** for a **laminar flow** = ?
252
Define H (**total** **head**)
**H = total head** - the **height** to which **fluid** **rises** in a **pitot tube** open to the **atmosphere**
253
What gives the **Energy Grade Line** a **negative** **gradient** along the flow?
**Frictional** **losses** give the **Energy Grade Line** a negative gradient along the flow
254
What is the **head** **loss**, hf?
The **head** **loss**, hf, is the **hydrostatic height difference** between two **horizontally** **connected** **reservoirs**
255
What is the **hydraulic head?**
The **hydraulic head** is the **sum** of the **pressure head** and the **elevation head**
256
Hhyd = ? (equation and definition)
Hhyd is the **height** to which **fluid rises** in a **piezometer**
257
What is a **piezometer?**
A **piezometer** is a **static** **pressure** **tap** with the **vertical** **tube** **open** to the **atmosphere**
258
What do **EGL** and **HGL** stand for?
EGL = Energy grade line
HGL = Hydraulic grade line
259
What does the **hydraulic grade line do?**
The **Hydraulic Grade Line** joins the **hydraulic head height** through a flow
260
The **Hydraulic Grade Line** is **below** the **Energy Grade Line** by...?
v2/2g
261
What is the formula used to calculate the **mass flow rate** through a pipe with **friction**? (A law _not_ a formula)
**Poiseuille’s Law**
262
For **laminar** **flow**, **Poiseuille's Law** = ?
263
Vm = ? (Poiseuille's law)
264
m dot = ? (Poiseuill's Law) so m dot = ?
m ̇ = *þ* vmA so =
265
For a circular pipe, A = ?
A = πD2/4
266
For **hydraulic pumping power, W =**?
267
For **uphill** **flow**, θ ? 0
θ \> 0
268
For **downhill** **flow**, θ ? 0
θ \< 0
269
For Poiseuilles law on inclined pipes, what do you add into these equations?
You add ***sin*θ**
270
If the pipe is not circularm we must use the **hydraulic diameter**, so Poiseuilles Law equations become?
Notice the **D2h** and **D4h**
271
For the **same free-stream velocity**, a **turbulent** **flow** will have a **much thicker boundary layer** than a...?
...**laminar flow**
272
The velocity gradient next to the wall is much higher in a...?
The wall shear stress is much higher in a...?
...**turbulent** **flow**
273
The **velocity profile** for a **laminar** **flow** is...?
...**parabolic in nature**
274
The **velocity profile** for a **turbulent** **flow** is...?
...much **fuller**, with a **sharp** **drop** near the **pipe wall**
275
The turbulent profile consists of four regions...(layers)
1. The viscous sublayer
2. The buffer layer
3. The overlap layer
4. The turbulent layer
276
What is the **viscous sublayer?**
***Viscous sublayer*** - the **thin layer** next to the wall where **viscous effects** are **dominant**
- The **velocity** **profile** in this layer is very nearly **linear**
277
What is the **Buffer layer?**
***Buffer layer*** - **turbulent** **effects** start to become **significant** but the **flow** is still **dominated** by **viscous** **effects**
278
What is the **overlap layer?**
***Overlap layer*** - **turbulent** **effects** are much **more** **significant**, but still **not yet dominant**
279
What is the **Turbulent** **layer**
***Turbulent layer*** - **turbulent** effects **dominate** over **viscous** **effects**
280
How do you approximate the **outer** **part** of the **turbulent** **velocity** **profile**? (Equation)
281
The **viscous** **sublayer** is usually less than...?
...**1%** of the **pipe diameter**
282
How to you **determine** the **friction** **factor** for a **turbulent pipe flow**?
By using the **Moody chart**
283
How do we use the **Moody chart**? (5 things)
1. Determine the **mean velocity** of the **pipe** **flow**
2. Determine the **Reynolds** **number**
3. Determine the **pipe** **relative** **roughness** ε/Dh
4. Read the **friction** **factor** from the Moody Chart
5. Evaluate the **pressure** **loss**
284
The **Fanning Friction Factor** is a factor of _ smaller than the **Darcy Friction Factor**.
So if a question comes up requiring the determination of a friction factor be sure to multiply the number obtained from the data book by...?
The **Fanning Friction Factor** is a factor of **_4_** smaller than the **Darcy Friction Factor**.
x4!
285
**Losses** in pipe systems fall into two catergories...?
**Major** and **Minor** **losses**
286
What are the **major losses** in engineering pipelines?
**Frictional losses**
287
What are the **minor losses** in long pipelines?
The **inlet, outlet, bends** and **valves**
288
In small pipe networks, separation losses due to bends, contractions, expansions may...?
...dominate the pressure loss in the system
289
Head losses for fittings in pipe systems can be determined by...? (Equations)
290
K in this equation is the...?
...**loss coefficient**
291
A sudden increase in pipe cross-section will produce loss in the system, what is the equation for this?
292
For a pipe flowing into a reservoir, *A2 *in this equation tends too...?
And so K = ?
A2 tends to infinity ∞
293
Losses in pipe inlets are driven by the curvature of the flow through the inlet
1. For a protruding inlet, K = ?
2. For a sharp-edged inlet, K = ?
3. For a rounded inlet, K tends to ____ as the radius of curvature of the inlet approaches \_\_\_\_
4. The value of K ____ as the inlet curvature \_\_\_\_
1. K = 1.0
2. K = 0.5
3. K tends to **_zero**_ as the radius of the curvature of the inlet approaches _**0.14D_**
4. The value of K **_changes**_ as the inlet curvature _**varies_**
294
The **smaller** the **vena** **contracta**, the...?
...**greater** the **flow** **separation** and the **higher** the value of K
295
As with the pipe inlet, the **loss coefficient** of the **bend** **depends** on its...?
... **radius** of **curvature**
296
The **sharper** the bend, the ____ the vena contracta and the ____ the loss coefficient becomes
The **sharper** the bend, the **_smaller_** the vena contracta and the **_higher_** the loss coefficient becomes
297
For a **mitre** **bend**,
r = ?
K ≈ ?
r = 0
K ≈ 1.1
298
For a flanged elbow bend,
K ≈ ?
K ≈ 0.3
299
**InvesFgated** the stability of submerged and **floaFng** bodies
**InvesFgated** the buoyant force
