Formulas

Question 1

Current Ratio

Answer 1

Question 2

Quick ratio

Answer 2

Question 3

Acid Test

Answer 3

Question 4

Inventory Turnover Ratio

Answer 4

Question 5

Value

Answer 5

Question 6

EBIT

Answer 6

Question 7

EBITDA

Answer 7

Question 8

Net Cash Flow

Answer 8

Question 9

NOWC

Answer 9

Question 10

Total net operating capital

Answer 10

Question 11

NOPAT

Answer 11

Question 12

FCF

Answer 12

Question 13

ROIC

Answer 13

Question 14

Capital Requirements ratio (CR)

Answer 14

Question 15

Operating profitability ratio (OP)

Answer 15

Question 16

MVA (2 different equations)

Answer 16

Market Value Added

Question 17

EVA (3 equations)

Answer 17

Question 18

Fixed assets turnover ratio

Answer 18

Question 19

Total Assets Turnover Ratio

Answer 19

Question 20

DSO

Answer 20

Days Sales Outstanding

Question 21

Debt ratio

Answer 21

Question 22

Liabilities-to-assets ratio

Answer 22

Question 23

Market debt ratio

Answer 23

Question 24

Equity multiplier

Answer 24

Question 25

TIE

Answer 25

Question 26

EBITDA coverage ratio

Answer 26

Question 27

Net Profit margin

Answer 27

aka 1) profit margin 2) profit margin on sales

Question 28

Operating profit margin

Answer 28

Question 29

Gross profit margin

Answer 29

Question 30

ROA (2 equations)

Answer 30

Return on total assets

Question 31

BEP

Answer 31

Basic earning power

Question 32

ROE (3 equations)

Answer 32

Return on Equity

Question 33

P/E

Answer 33

Question 34

P/CF

Answer 34

Price/cash flow ratio

Question 35

BVPS

Answer 35

Book value per share

Question 36

M/B

Answer 36

Market/book ratio

Question 37

FV_N

Answer 37

Question 38

PV

Answer 38

Question 39

PV of a perpetuity

Answer 39

Question 40

FVA_N

Answer 40

Question 41

FVADue

Answer 41

Question 42

PVA_N

Answer 42

Question 43

PVA_Due

Answer 43

Question 44

PV_{Uneven stream}

Answer 44

Question 45

FV_{Uneven stream}

Answer 45

Question 46

I_PER

Answer 46

Question 47

APR

Answer 47

Question 48

FV_N

Answer 48

Question 49

Number of periods

Answer 49

Question 50

EFF%

Answer 50

aka EAR%

Question 51

V_B

Answer 51

Question 52

Semiannual payments: V_B

Answer 52

Question 53

Yield to maturity: Bond price =

Answer 53

This rate is called the bond’s yield to maturity (YTM), and it is the interest rate generally discussed by investors when they talk about rates of return. **The yield to maturity is usually the same as the market rate of interest, r_d.**

Question 54

Price of callable bond (if called at N)

Answer 54

Question 55

Current yield

Answer 55

Question 56

Yield to Maturity: Bond Price

Answer 56

Question 57

define r_d

Answer 57

from p. 215

Question 58

IP_N

Answer 58

the inflation rate built into a 30-year bond is the **average rate of inflation** expected over the next 30 years. If It is the expected inflation during year t, then the inflation premium for an N-year bond’s yield (IPN) can be approximated as:

Question 59

Expected rate of return for a portfolio where you are given the expected rates of return for each item in the portfolio

Answer 59

The weights are the probabilities, and the weighted average is the expected rate of return (r_hat), called “r-hat,” which is the mean of the probability distribution Here r_i is the return if outcome i occurs, p_i is the probability that outcome i occurs, and n is the number of possible outcomes. Thus, r-hat is a weighted average of the possible outcomes (the r_i values), with each outcome’s weight being its probability of occurrence.

Question 60

Historical average for r

Answer 60

Question 61

Variance of "r" with weighted scenarios

Answer 61

verify: In statistics the hat symbol (e.g. p-hat) denotes the mean of a sample vice the mean of population.

Question 62

Standard deviation of "r" with weighted scenarios

Answer 62

Question 63

Historical estimated σ

Answer 63

Question 64

r(hat)_p

Answer 64

Question 65

Calculate σ_p by using r_i

Answer 65

Question 66

Historical estimated rho

Answer 66

rho = R

Question 67

COV_iM

Answer 67

Question 68

b_i

Answer 68

Question 69

b_p

Answer 69

Question 70

Market risk premium

Answer 70

Question 71

RP_i

Answer 71

Question 72

SML

Answer 72

Question 73

Fama-French

Answer 73

Question 74

Predicted return based on Fama-French model

Answer 74

Predicted return = a_i + b_i(r_M,t) + c_i(r_SMB,t) + d_i(r_HML,t)

Question 75

Operating Cost of Capital

Answer 75

Operating Capital x WACC From EVA equation

Question 76

3 equations that have EBIT in the numerator

Answer 76

1) Operating Profit Margin = EBIT/Sales 2) BEP (i.e. Basic Earning Power) = EBIT/TA 3) TIE (i.e. Times Interest Earned) = EBIT/Interest

Question 77

Estimated Stock Price (via Intrinsic Stock Price)

Answer 77

**Total Intrinsic Value** = V_OP + Sht-term Inv. = V_OP + Value of nonoperating assets **Intrinsic Value of equity** = Total Intrinsic Value - All Debt - PS where PS = P.Stock **Intrinsic Stock Price** = (Intrinsic VoE) / CSO where VoE = Value of equity \*\*There is practice problem at the bottom of p. 302 that asks for the "estimated price per share" wherein one must use the Intrinsic Stock Price formula to derive the answer. \*\*Also, there is a picture on p. 303 that depicts the steps for calculating the "Estimated intrinsic stock price".

Question 78

Estimate the FCF at time "t" with a constant growth rate

Answer 78

FCF_t = FCFx(1 + g_L)^t-x (eqn 7-7 from p. 304)

Question 79

List the common mistakes when applying the Constant growth model.

Answer 79

**If growth is greater than the cost of capital, you must use the multistage model.**

Question 80

Describe the 4 steps of the Multistage Model: Valuation When Expected Short-Term Free Cash Flow Grows at a Nonconstant Rate

Answer 80

**Step 1**: Because the short-term growth rates are nonconstant, we cannot immediately apply the constant growth model from the previous section. However, we can use the multi-stage valuation model to estimate the value of operations, as described in the following steps: **Step 2**: Forecast expected free cash flows and calculate the annual growth rates for each year in the forecast. **Continue forecasting additional years until the growth rate in FCF is expected to become constant.** The last year in the forecast is called the forecast horizon. It is also called the horizon date or the terminal date (because it is at the end of the explicit forecast, not because the free cash flows terminate). For companies in mature, highly competitive markets, you may need to forecast only a few years. For companies in high-growth industries, you may need to forecast 15 to 25 years. **Step 3**: immediately after receiving the FCF at the horizon date. This is also called the terminal value (because it is at the end of the explicit forecast) or the continuing value (because it is the value if the operating assets continue to be used rather than be liquidated). **Step 4**: Create a time line with the free cash flows for each year up to the horizon date. The time line should also include the horizon value at the horizon date. This means there will be two cash flows on the horizon date, the free cash flow for that year and the previously calculated horizon value. Discount the cash flows in the time line using the weighted average cost of capital. The result is the estimated value of operations as of t = 0.

Question 81

Multistage Model equation

Answer 81

Question 82

Multistage Model equation diagram

Answer 82

Question 83

Describe the steps (i.e. the inputs) for using a financial calculator to derive the V_OP for uneven CFs that involve a Horizon value.

Answer 83

The **_sum_** of the last CF (in the uneven series) plus the Horizon value should be entered as one value in the last CF entry on your financial calculator. **Example problem:** A company expects FCF of -$10 million at Year 1 and FCF of $20 million at Year 2; after Year 2, FCF is expected to grow at a 5% rate. If the WACC is 10%, then what is the horizon value of operations, Vop(Year 2)? (**$420 million**) What is the current value of operations, Vop(Year 0)? (**$354.55 million)**

Question 84

Find the value of operations at one year prior to "t".

Answer 84

Simply omit the (1 + g_L) multiple of FCF_t which would normally be used to find FCF_t+1

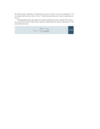
Question 85

1) Cathey Corporation currently has sales of $1,000, which are expected to grow by 10% from Year 0 to Year 1 and by 4% from Year 1 to Year 2. The company currently has an operating profitability ratio (OP) of 7% and a capital requirement ratio (CR) of 50% and expects to maintain these ratios at their current levels. The current level of total net operating capital (OpCap) is $510. Use these inputs to forecast free cash flow (FCF) for Years 1 and 2. (Hint: You must first forecast sales, net operating profit after taxes (NOPAT), and total net operating capital (OpCap) for each year.) 2) Cathey Corporation has a 12% weighted average cost of capital. Cathey’s free cash flows, estimated in the previous question, are expected to grow at 4% beginning at Year 2 and thereafter. What is the horizon value (use Year 2 for the horizon)? What is the current value of operations? 3) Cathey Corporation has $80 in short-term investments, $20 in short-term debt, $140 in long-term debt, $30 in preferred stock, and 10 shares of common stock outstanding. Use the value of operations from the previous question to estimate the intrinsic common stock price per share.

Answer 85

1) (**$37.00 and $58.08)** ## Footnote **2)** (**$755.04 and $681.25)** **3)** (**$57.13)** Steps: 1. Project Sales with growth rate given. 2. Derive NOPAT from the given OP ratio and Sales data. 3. Project NOPAT w/ the same growth rate as the Sales data. 4. Project OpCp by using the already projected Sales data while maintaining the constant CR (Capital Requirements) ratio. 5. Calculate FCF₁ = NOPAT₁ - (OpCp₁ - OpCp₀) 6. Calculate FCF₂ = NOPAT₂ - (OpCp₂ - OpCp₁)

Question 86

V_OP

Answer 86

Question 87

FCF_t within a stream of CFs that involve constant growth.

Answer 87

FCF_t = FCF_x(1+g_L)^t-x

Question 88

V_OP (constant growth)

Answer 88

p. 305 (yellow highlight) dictates to NOT use this formula if g_L \> WACC bc this results in (-) V_OP which is "impossible".

Question 89

V_OP (for a perpetuity)

Answer 89

FCF / WACC

Question 90

Horizon Value (at time t)

Answer 90

Question 91

Total intrinsic entity value

Answer 91

TIEnV = V_OP + Value of nonoperating assets = V_OP + Sht.I where Sht.I = Short-term Investments

Question 92

Intrinsic Value of Equity

Answer 92

IVE = TIEnV - PS - D

Question 93

ISP (Intrinsic Stock Price)

Answer 93

ISP = IVE / CSO IVE = TIEnV - PS - D TIEnV = V_op + V_NOA where V_NOA = Value of nonoperating assets = VOP + Sht.I where Sht.I = Short-term Investments {this was NOT on the formula sheet, but it worked in the problems}

Question 94

V_OP (at Horizon Year T) {2 equations}

Answer 94

Question 95

P(hat)₀ = PV of expected future dividends that are nonconstant

Answer 95

Question 96

Find P₀(hat) for a stock with constant growing dividends

Answer 96

Question 97

Constant growth of r_s(hat)

Answer 97

Question 98

Expected dividend yield

Answer 98

D₁ / P₀

Question 99

Expected capital gains yield

Answer 99

Question 100

Expected rate of return on stock

Answer 100

Question 101

r_s(bar)

Answer 101

Actual dividend yield + Actual captial gains yield

Question 102

For a zero growth stock, P₀(hat)

Answer 102

D / r_s

Question 103

Horizon value of stock

Answer 103

Question 104

V_ps

Answer 104

Question 105

r_ps(hat)

Answer 105

Question 106

Explain the pattern for the constant growth formula

Answer 106

Use the 2nd repetitive CF (in series of constant growth) in the numerator. This works for both FCF and Dividends even though the notation is slightly different. For dividends, realize that the problem might provide an expected dividend one year (or period) from today that will grow at a constant rate (g_L). This dividend (D₁) is the dividend value you should input into the formula for P₀(hat) even though the problem might provide only D₁ data. See example below. ----------- A stock is expected to pay a dividend of $2 at the end of the year. The required rate of return is r_s = 12%. What would the stock’s price be if the constant growth rate in dividends were 4%? (**$25.00)** What would the price be if g = 0%? (**$16.67**)

Question 107

If given D₀, and you are asked to calculate P₀(hat) with a series of future dividends, EXCLUDE D₀ from your CF inputs such that CF₀ = 0.

Question 108

1) Dodd Corporation is a private company that earned $4.00 per share for the most recent year. If the average P/E ratio of a group of comparable public companies is 11, what is an estimate of Dodd’s stock value on a per share basis? 2) The company in the previous question, Dodd Corporation, has 100,000 shares of common stock owned by its founder. Dodd owes $1,300,000 to its bank. Dodd has 11,400 customers. If the average ratio of total entity value to customers is $500 for a group of comparable public companies, what is Dodd’s estimated total entity value? 3) What is its estimated stock value on a per share basis?

Answer 108

1) (**$44.00**) 2) **($5,700,000**) 3) (**$44.00**) For question #2, when trying to find the "estimated stock value on a per share basis", use the following: IPS = IVE / CSO IVE = TIEnV - PS - D TIEnV is given by solving part "a" of questions #2.

Question 109

time value

Answer 109

the difference between the option's price and it's exercise value (p. 346)

Question 110

Exercise value

Answer 110

MAX[Current price of stock - Strike price,0]

Question 111

In terms of PV_RFP : V_c

Answer 111

V_C = Value of Call Option V_c = N_S(P) - PVRFP PV_RFP = PV of [N_sP(u) - C_u]

Question 112

Hedge portfolio's payoff if stock is up

Answer 112

Hedge portfolio's payoff if stock is up = N_sP(u) - C_u

Question 113

Hedge portfolio's payoff if stock is down

Answer 113

Hedge portfolio's payoff if stock is down = N_sP(d) - C_d

Question 114

1) Lett Incorporated’s stock price is now $50, but it is expected either to rise by a factor of 1.5 or to fall by a factor of 0.7 by the end of the year. There is a call option on Lett’s stock with a strike price of $55 and an expiration date 1 year from now. What are the stock’s possible prices at the end of the year? 2) What is the call option’s payoff if the stock price goes up? 3) If the stock price goes down? 4) If we sell 1 call option, how many shares of Lett’s stock must we buy to create a riskless hedged portfolio consisting of the option position and the stock? 5) What is the payoff of this portfolio? ( **6)** If the annual risk-free rate is 6%, then how much is the riskless portfolio worth today (assuming daily compounding)? **7)** What is the current value of the call option?

Answer 114

1) **($75 or $35)** ## Footnote **2) ($20)** **3) ($0)** **4) (0.5)** **5) $17.50)** **6)** (**$16.48)** **7)** (**$8.52**)

Question 115

When constructing a hedge portfolio and deriving the PV, the input of 1) FV = ? 2) I/Y = ?

Answer 115

1) FV = N_S\*P(u) - C_u = N_s\*P(d) - C_{d 2) I/Y =} r_RF \* t / 365 **a) (be sure to input the percentage rate 6 for 6% vice 0.06)** **b) remember to use daily or continuous compounding for options**

Question 116

To discount a value by the continuously compounded risk-free rate, multiply by \_\_\_\_\_.

Answer 116

e^-r_RFt

Question 117

V_{put option}

Answer 117

V_{put option} = V_C - P +Xe^-r_RFt

Question 118

Exercise value

Answer 118

MAX[Current stock price - Strike Price,0]

Question 119

time value

Answer 119

option's price - exercise value The time value of the option represents the **extra amount over the option's immediate exercise value** that a purchaser will pay for the chance the stock price will appreciate over time.

Question 120

When using a risk-free portfolio: V_C

Answer 120

Ns(P) - PV_RFP

Question 121

Number of stock shares in hedged portfolio

Answer 121

N = (Cu - Cd) / (P(u-d))

Question 122

Variables used in Black-Scholes OPM (Options Pricing Model)

Answer 122

Question 123

Black-Scholes OPM: V_C

Answer 123

Question 124

Black-Scholes OPM: d₁

Answer 124

Question 125

Black-Scholes OPM: d₂

Answer 125

Question 126

Put-call parity: Put option =

Answer 126

Question 127

Black-Scholes: V_put

Answer 127

Question 128

Net Issue price for bonds?? (p. 380)

Answer 128

M(1 - F)

Question 129

r_PS with component cost of PS (i.e. flotation costs)

Answer 129

Question 130

Market equilibrium

Answer 130

Expected rate of return = required rate of return

Question 131

Rep / Div

Answer 131

Question 132

Using Rep/Div what is r_M

Answer 132

Question 133

Own-bond yield-plus-judgmental-risk-premium: r_S

Answer 133

Question 134

retention growth eqn. g = ?

Answer 134

Question 135

cost of new external common equity

Answer 135

Question 136

WACC

Answer 136

Question 137

NPV

Answer 137

Question 138

IRR

Answer 138

Question 139

MIRR

Answer 139

Question 140

PI

Answer 140

Question 141

Payback

Answer 141

Question 142

Current Value of hedge portfolio

Answer 142

Current value of hedge portfolio = Present value of riskless payoff N_S(P) - V_C = Present value of riskless payoff (p. 351)

Question 143

1) Hedge portfolio's payoff if stock is up 2) Hedge portfolio's payoff if stock is down

Answer 143

1) NsP(u) - Cu 2) NsP(d) - Cd

Question 144

Binomial method: V_c

Answer 144

Question 145

Black-Scholes: V_put

Answer 145

Question 146

Payout ratio

Answer 146

Dividends / NI DPS / EPS

Question 147

Retention Ratio

Answer 147

Addition to RE / NI = 1 - Payout ratio

Question 148

How to find MIRR, IRR, NPV, and NFV using the TI BAII Plus Professional

Answer 148

see p. 427 for the following example ## Footnote Project: _0_ _1_ _2_ A -1,000 1,150 100 B -1,000 100 1,300 The cost of capital is 10%. What are the projects’ IRRs, MIRRs, and NPVs? (IRR_A = 23.1%, IRR_B = 19.1%; MIRR_A = 16.8%, MIRR_{B =} 518.7%; NPV_A = $128.10, NPV_B = $165.29) When using the TI BAII Plus Professional, use must compute (i.e. hit the "CPT" button) IRR, before the calculator will actuall hit the down arrow to get to the MIRR (i.e. "MOD") option. Note that you will have to input the reinvestment rate (i.e. "RI") value and hit "enter" before the "MOD" screen appears.

Question 149

1) A project has the following expected cash flows: CF₀ = -$500, CF₁ = $200, CF₂ = $200, and CF₃ = $400. If the project’s cost of capital is 9%, what is the PI?

Answer 149

1) **(1.32)** When calculating PI (profitability index), be sure to use the PV of future CFs that start with the end of year 1 =\> CF₀ = 0. This is in contrast to finding the NPV where CF₀ incorporates the cost of the project.

Question 150

Calculate the **component cost** of debt, PS, and CS

Answer 150

Question 151

question #4 from the attached image

Answer 151

5.41%

Question 152

question #7 from the attached image

Answer 152

Question 153

question #11 from the attached image

Answer 153

answer = **8.02%** use PV = -4.42 FV = 6.5 N = 5 PMT = 0 then "CPT" "I/Y"

Question 154

problem #12b from attached image

Answer 154

don't use the hint; just use the growth rate already calculated from part "a"

Question 155

Project Cash Flow

Answer 155

Question 156

Expected NPV (from a portfolio with multiple NPVs)

Answer 156

Question 157

σ_NPV (from a portfolio with multiple NPVs)

Answer 157

Question 158

CV_NPV

Answer 158

Question 159

AFN | (2 equations)

Answer 159

Question 160

Self-supporting g

Answer 160

Question 161

Full Capacity Sales | (3 interrelated eqns.)

Answer 161

1) Full Capacity Sales 2) (Target fixed assets) / Sales 3) Required level of fixed assets

Question 162

(Target fixed assets) / Sales

Answer 162

Question 163

Required level of fixed assets

Answer 163

Question 164

Residual Distribution

Answer 164

If a firm rigidly follows the residual distribution policy, then distributions paid in any given year can be expressed as follows: Distributions = NI - Add. to RE needed to finance new investments Distributions = NI - (Target equity ratio)(Total capital budget) [p. 574]

Question 165

1) Hamilton Corporation has a target equity ratio of 65%, and its forecasted capital budget is $2 million. If Hamilton has net income of $1.6 million and follows a residual distribution model, how much will its distribution be?

Answer 165

1) **$300,000)** **Distributions** = Net income - Additions to retained earnings needed to finance new investments **Distributions** = Net income - [(Target equity ratio) \* (Total capital budget)]

Question 166

1) A firm’s most recent FCF was $2.4 million, and its FCF is expected to grow at a constant rate of 5%. The firm’s WACC is 14%, and it has 2 million shares outstanding. The firm has $12 million in short-term investments that it plans to liquidate and then distribute in a stock repurchase; the firm has no other financial investments or debt. Verify that the value of operations is \_\_\_\_\_\_\_. 2) Immediately prior to the repurchase, what are the intrinsic value of equity and the intrinsic stock price? 3) How many shares will be repurchased? 4) How many shares will remain after the repurchase? 5) Immediately after the repurchase, what are the intrinsic value of equity and the intrinsic stock price?

Answer 166

1) **$28 million**. 2) **($40 million; $20/share)** 3) **0.6 million** 4) **(1.4 million)** **5) (*$28 million*; $20/share).** ***Review p. 585 to understand why the IVE decreases* by the amount of Cash used for repurchases.** The V_OP = HV. Note that the **multistage model is NOT used** bc the initial FCF used in the constant growth model is not occuring immediately or in the future, but instead has already occurred in the past. Therefore, the V_OP is simply equal to the Horizon Value. ***p. 582 (bright green highlight) explicitly states that the "repurchase does not change the stock price."***

Question 167

Residual Distribution | (2 equations)

Answer 167

1) Residual Distributions = NI - Add. to RE needed to finance new investments 2) Residual Distributions = NI - [(Target equity ratio) x (Total capital budget)]

Question 168

Number of shares repurchased (where repurchased shares are a form of distribution)

Answer 168

Question 169

n_Post

Answer 169

Question 170

Capital Budget appears to equal OpCp

Question 171

1) Suppose you have 1,000 common shares of Burnside Bakeries. The EPS is $6.00, the DPS is $3.00, and the stock sells for $90 per share. Burnside announces a 3-for-1 split. Immediately after the split, how many shares will you have? 2**)** What will the adjusted EPS and DPS be? 3) What would you expect the stock price to be?

Answer 171

1) (**3,000)** 2) **$2 and $1)** 3) **$30)**

Question 172

Operating break-even point

Answer 172

The operating break-even point occurs when EBIT = 0. EBIT = PQ - VQ - F = 0 P = Price Q = Quantity V = Variable costs per unit F = Fixed costs

Question 173

1) A firm’s value of operations is equal to $800 million *_after_* a recapitalization. (The firm had no debt before the recap.) The firm raised $200 million in new debt and used this to buy back stock. The firm had no short-term investments before or after the recap. After the recap, w_d = 25%. The firm had 10 million shares before the recap. Its federal-plus-state tax rate is 25%. What is S (the value of equity after the recap)? 2) What is P_Post (the stock price after the recap)? 3) What is n_Post (the number of remaining shares after the recap)? **Note:** The firm will still have the debt after the recap., and it will pay off that debt over time. The funds raised from the issue of debt will be used to repurchase stock**.**

Answer 173

1) **($600 million)** 2) **($80/share**) 3) **7.5 million)** IVE = S = TIEnV - PS - D TIEnV = V_op + V_NOA where V_NOA includes short-term investments 1) After the recap, S = 800M - 200M = **600M** 2) bc P_Post = P_Prior : P_Post = 800M / 10M = **$80/share** 3) bc n_Prior - n_Post = (D_new - D_Old) / P_Prior =\> n_Post = n_Prior - (D_new - D_Old) / P_Prior n_Post = 10M - (200M / 80) = **7.5M**

Question 174

Formula for calcuting I/Y when given PV, FV, and N

Answer 174

Question 175

EBIT (w/ Q for Quantity)

Answer 175

Question 176

Break Even Quantity

Answer 176

Question 177

Miller, corporate and personal taxes, V_L

Answer 177

Here T_c is the corporate tax rate, T_s is the effective personal tax rate on income from stocks, and T_d is the tax rate on income from debt.

Question 178

Hamada: leveraged beta = b

Answer 178

S = MVE in formula D = Market value of debt [p. 624)

Question 179

Hamada: unleveraged beta = b_u

Answer 179

Question 180

r_s (include business risk and financial risk)

Answer 180

**business risk** - The risk inherent in the operations of the firm, prior to the financing decision. Thus, business risk is the uncertainty inherent in future operating income or earnings before interest and taxes. Business risk is caused by many factors; two of the most important are sales variability and operating leverage. **financial risk** The risk added by the use of debt financing. Debt financing increases the variability of earnings before taxes (but after interest); thus, along with business risk, it contributes to the uncertainty of net income and earnings per share. Business risk plus financial risk equals total corporate risk.

Question 181

If g=0: V_op (3 equations)

Answer 181

Question 182

Total Corporate Value

Answer 182

This equation implies that Total corporate value = TIEnV where TIEnV = Total Intrinsic Entity Value

Question 183

S | (2 equations)

Answer 183

bc S = TCV - Value of all debt, w_d in the equation below must? incorporate both long-term debt and short-term debt. [TCV = Total Corporate Value]. ?? Ask Professor Cudd why the equation S = (1 - w_d)V_op does NOT include V_noa??

Question 184

D

Answer 184

Question 185

Cash raised by issuing debt

Answer 185

Question 186

P_{prior (2 equations)}

Answer 186

P_prior = P_post P_prior = S_prior / n_prior

Question 187

n_post | (2 equations)

Answer 187

Question 188

P_post | (2 equations)

Answer 188

Question 189

V₀ (verify: I believe the subscript is a zero)

Answer 189

Question 190

EPS

Answer 190

Question 191

NI

Answer 191

Question 192

ICP

Answer 192

ICP = Inventory Conversion Period

Question 193

ACP

Answer 193

ACP = Average Collection Period

Question 194

PDP

Answer 194

PDP = Payables Deferral Period

Question 195

CCC

Answer 195

CCC = Cash Conversion Cycle

Question 196

AR ## Footnote (verify: 2 equations for AR; on the equation sheet, one equation is listed as "Accounts Receivable", and one is listed simply as "receivables"

Answer 196

AR = Accounts Receivable

Question 197

Receivables ## Footnote (verify: 2 equations for AR; on the equation sheet, one equation is listed as "Accounts Receivable", and one is listed simply as "receivables")

Answer 197

Question 198

Nominal annual cost of trade credit

Answer 198

Question 199

Effective cost of trade credit

Answer 199

[(1 + (finance charge / true price))^(365/(dco - dp)) - 1]

Question 200

1) A company has annual sales of $730 million. If its DSO is 35, what is its average accounts receivables balance?

Answer 200

1) **($70 million)**

Question 201

1) A company buys on terms of 2/12, net 28. What is its nominal cost of trade credit? ( 2) The effective cost?

Answer 201

1) **46.6%)** **2) (58.5%)** **dco** = days credit is outstanding = the number after "net" =\> for 2/10 net 30 =\> dco = 30 **dp** = discount period = the number after the slash =\> for 2/10 net 30 =\> dp = 10 **tp** = true price = 100 - discount % **fc** = finance charge = discount % **\* note that (discount %) / (100 - discount %) = finance charge / true price = fc / tp** 1) Nominal cost of trade credit = [2/(100-2) \* 365/(28-12) = **46.56%** 2) Effective cost of trade credit = [(1 + (fc / tp)^(365 / (dco - dp)) - 1] = [(1 + (2/98)^(365 / (28 - 12)) - 1] = **58.5%**

Question 202

free trade credit vs costly trade credit

Answer 202

PCC buys 73,000 of these chips a year. If PCC pays in 10 days and takes the discount, its accounts payable balance will be the discount purchases per day multiplied by the 10 days, which is $98(73,000/365)(10 days) = **$196,000**. This amount is called **_free trade credit_** since PCC doesn’t have to pay anything to receive this trade credit. If PCC, instead, pays in 30 days, then its accounts payable balance will be $98(73,000/365)(30 days) = $588,000. This additional accounts payable balance, $588,000 - $196,000 = **$392,000,** is called costly trade credit because PCC must pay an effective rate of 44.6% to receive it. In this case, the **_costly trade credit_** is very costly indeed! **verify: For costly trade credit, why is the discount price of $98 used instead of the non-discount price of $100?**

Question 203

1) Simple Interest rate per day 2) Interest charge for month using simple interest

Answer 203

1) Simple Interest rate per day = (Nomial rate) / 365 2) Interest charge for month using simple interest = (Rate per day)(Days in month)(Amount of loan)

Question 204

1) If a firm borrowed $500,000 at a rate of 10% simple interest with monthly interest payments and a 365-day year, what would be the required interest payment for a 30-day month? **2)** If interest must be paid monthly, what would be the effective annual rate? 3) If this loan had been made on a 10% add-on basis, *_payable in 12 end-of-month installments,_* what would be the monthly payment amount? 4) What is the annual percentage rate? 5) The effective annual rate? [p. 683]

Answer 204

1) (.1 / 365)(30 days)(500,00) = $**4,109.59** 2) EFF% = (1 + .1 / 12)^12 - 1 = **10.47**% 3) 500,00(1.10) / 12 = $**45,833.33** 4) Using financial calc: FV = 0 PV = 500,000 PMT = -45,833 N = 12 [CPT I/Y] =\> **I/Y = 1.4975** ; Then multiply I/Y = 1.4975 by 12 = **17.97%** 5) EFF% = (1 + .014975)^12 - 1 = 0.19526 = **19.53%**

Question 205

1) Assume that the indirect quote is for 10.0 Mexican pesos per U.S. dollar. What is the direct quote for dollars per peso? 2) Assume that the indirect quote is for 115 Japanese yen per U.S. dollar and that the direct quote is for 1.25 U.S. dollars per euro. What is the yen per euro exchange rate?

Answer 205

1) **(0.10 dollars per peso)** 2) **143.75 yen per euro)**

Question 206

1) What is interest rate parity? 2) Assume that interest rate parity holds. When a currency trades at a forward premium, what does that imply about domestic rates relative to foreign interest rates? What does it imply when a currency trades at a forward discount? 3) Assume that 90-day U.S. securities have a 4.5% annualized interest rate, whereas 90-day Swiss securities have a 5% annualized interest rate. In the spot market, 1 U.S. dollar can be exchanged for 1.2 Swiss francs. If interest rate parity holds, what is the 90-day forward rate exchange between U.S. dollars and Swiss francs? 4) On the basis of your answer to the previous question, is the Swiss franc selling at a premium or discount on the forward rate? **[p. 721]**

Answer 206

1) Interest rate parity means that investors should expect to earn the same return on security investments in all countries after adjusting for risk. 2) If a dollar buys more of the foreign currency in the spot market than in the forward market, then the foreign currency is appreciating. Therefore, the **_forward foreign currency_** is selling at a **premium**. [p. 718] 3) **(0.8323 $ per SFr or 1.2015 SFr per $)** 4) (**Discount)**

Question 207

FOREX: direct quote

Answer 207

**_direct quote_** - When discussing exchange rates, the number of U.S. dollars required to purchase one unit of a foreign currency. For example, EUR/USD 1.20 is a direct quote meaning that the rate is 1.20 dollars per euro.

Question 208

FOREX: indirect quote

Answer 208

**_indirect quote_** - When discussing exchange rates,the number of units of foreign currency that can be purchased for one unit of home currency. For example, from the U.S. perspective, USD/JPN 80 is an indirect quote meaning that the rate is 80 yen per dollar.

Question 209

Single-period interest rate parity

Answer 209

Question 210

Expected t-year forward exchange rate

Answer 210

Question 211

P_h

Answer 211

Question 212

Spot rate

Answer 212

Note that the **spot rate** is expressed as a **direct rate**; it is the **number of units of home currency** that can be exchanged for **one unit of foreighn currency.**

Question 213

1) A computer sells for $1,500 U.S. dollars. In the spot market, $1 = 115 Japanese yen. If purchasing power parity holds, what should be the price (in yen) of the same computer in Japan?

Answer 213

**(¥172,500)**

Question 214

The current exchange rate is 1.1 dollars per euro. A 5-year U.S. government bond has a 3% yield, and a 5-year French government bond has a yield of 4%. What is the expected 5-year forward rate?

Answer 214

EX_forward = 1.1 \* (1.03 / 1.04)^5 = **(1.0481 dollars per euro)** Note that the annualized rates are left as given in contrast to, for example, 90 day securities that must have either r_h or r_f multiplied by (90/365).

Question 216

Do the Interest rate parity problems from the image below:

Question 217

Amount left on the table

Answer 217

Question 218

Percentage shares owned by new investors

Answer 218

Question 219

n_new

Answer 219

Question 220

V_Post-IPO

Answer 220

Question 221

P_Offer

Answer 221

Question 222

% of shares required by new investors ## Footnote [p. 756] new investors expect to own a % of the company's shares equal to the % of the company's value they provide

Answer 222

Question 223

1) A privately held company has an estimated value of equity equal to $100 million. The founders own 10 million shares. If the company goes public and sells 1 million shares with no underwriting costs, how much should the per share offer price be? 2) If instead the underwriting spread is 7%, what should the offer price be?

Answer 223

1) ($10.00) 2) ($9.93)