Formulas, etc Flashcards
(32 cards)
1
Q

A

2
Q

A

3
Q
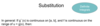
A

4
Q

A

5
Q

A

6
Q

A

7
Q
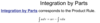
A

8
Q

A
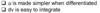
9
Q
Integration by Parts
A
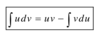
10
Q
Integration by Parts - Steps
A

11
Q
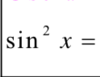
A
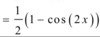
12
Q
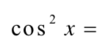
A
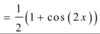
13
Q

A

14
Q
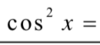
A

15
Q
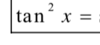
A
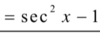
16
Q

A

17
Q

A

18
Q

A

19
Q

A

20
Q

A

21
Q

A

22
Q

A

23
Q

A

24
Q

A

25


26
To perform a PFD
Degree of the Numerator \< Degree of the Denominator.
If it is not, one must perform long division first.
Q(x) must be factored completely:
only linear and/or irreducible quadratic factors.
27
Case I: Q(x) is the product of distinct linear factors.

28
Case II: Q(x) is the product of linear factors where some are repeated.

29
Case III: Q(x) contains irreducible quadratic factors that are not repeated.

30
Case IV: Q(x) contains a repeated irreducible quadratic factors.

31
Determine the coefficients - Method 1: Substitute in (1) values of x. Start with the roots of Q(x)


32
Determine the coefficients:
Method 2: Expand the right hand side of (1), collect like terms and match the coefficients of the powers of x.




