Geometry

Question 1

What is the Diameter and Radius of the following circle?

Answer 1

Diameter = 12 in

r = (d)/2

r = 12/2

r = 6

Radius = 6 in

Question 2

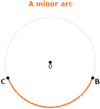
Minor Arc

Answer 2

An arc of a circle whose measure is less than 180°.

Question 3

The Diameter of a circle is 16 units.

What is the Radius of the circle?

Answer 3

r = (d)/2

r = (16)/2

r = 8

Radius = 8 Units

Question 4

Tangent

Answer 4

A straight line or plane that just touches a curve at one point.

Question 5

What is the diameter of the circle below?

Answer 5

d = (c)/π

d = 10/π

d = 3.18

Diameter = 3.18m

Question 6

Secant

Answer 6

A line that intersects the curve in at least two (Distinct) points.

Question 7

π (PI)

(Definition)

Answer 7

The ratio of the Circumference of a circle to its Diameter (3.142)

Question 8

A circle has a circumference of 907.46 units and a diameter of 289 Units.

What is the ratio of the Circumference to the diameter?

Answer 8

π = c/d

π = 907.46/289

π = 3.14 Units

Question 9

What is the Radius and Diameter of the following circle?

Answer 9

Radius = 8 ft

d = 2(r)

d = 2(8)

d = 16

Diameter = 16 ft

Question 10

Circumference (From Radius and π)

(Equation)

Answer 10

c = 2πr

Question 11

Suppose the radius of a circle is 3 units.

What is the Circumference?

Answer 11

c = 2π(r)

c = 2π(3)

c = 6π

Circumference = 18.85 Units

Question 12

Radius (From Diameter)

Equation

Answer 12

r = d/2

Question 13

π (From Circumference and Radius)

(Equation)

Answer 13

π = c/2r

Question 14

Chord

Answer 14

A line segment connecting two points on a curve.

Question 15

Diameter

(Definition)

Answer 15

Any straight line segment that passes through the center of the circle and whose endpoints lie on the circle.

Question 16

Arc Length

(Equations)

Answer 16

Arc Length = (Central Angle/ 360°) Circumference

Question 17

Radius (From π and Circumference)

(Equation)

Answer 17

r = c/2π

Question 18

A circle has the circumference of 153.86 units.

What is the radius of the circle?

Answer 18

r = (c)/2π

r = (153.86)/6.28

r = 24.5

Radius = 24.5 Units

Question 19

Circle

Answer 19

The locus of all points equidistant from a central point.

Question 20

Circumference (From Arc Length and Central Angle)

(Equations)

Answer 20

Circumference = (360° / Central Angle) (Arc Length)

Question 21

Circumference (From Diameter and π)

(Equation)

Answer 21

c = dπ

Question 22

Central angle

(Equations)

Answer 22

Central Angle = (Arc length/ Circumference) (360°)

Question 24

Arc Length

(Definition)

Answer 24

A portion of the circumference of the circle.

Question 25

Suppose the diameter of a circle is 6 units. What is the Circumference?

Answer 25

c = dπ c = (6)π c = 18.85 Circumference = 18.85 Units

Question 26

Major Arc

Answer 26

An arc of a circle whose measure is greater than 180°.

Question 27

Diameter (From π and Circumference) | (Equation)

Answer 27

d = c/π

Question 28

π (From Circumference and Diameter) | (Equation)

Answer 28

π = c/d

Question 29

A circle has a Circumference of 50.24 Units and a Radius of 8 units. What is the ratio from the Circumference to the diameter?

Answer 29

π = c/2r π = 50.24/16 π = 3.14

Question 30

Arc Measure | (Definition)

Answer 30

The measure of the central angle that intercepts an arc, measured in degrees.

Question 31

The Radius of a circle is 2 units. What is the Diameter of the circle?

Answer 31

d = 2(r) d = (2)2 d = 4 Diameter = 4 Units

Question 32

Radius | (Definition)

Answer 32

A straight line from the center to the circumference of a circle or sphere.

Question 33

Diameter (From Radius) Equation

Answer 33

d = 2r

Question 34

Circumference | (Definition)

Answer 34

The distance around a circle.