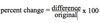GRE Numbers Flashcards
Prime numbers less than 30
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
An integer is divisible by 2 if…
…its units digit is divisible by 2.
An integer is divisible by 3 if…
…the sum of its digits are divisible by 3.
An integer is divisible by 4 if…
…its last two digits form a number that’s divisible by 4. Thus, 712 is div. by 4 b/c 12 is div. by 4.
An integer is divisible by 5 if…
…its units digit is either 0 or 5.
An integer is divisible by 6 if…
…it is divisible by both 2 and 3.
An integer is divisible by 9 if…
…the sum of its digits is divisible by 9.
An integer is divisible by 10 if…
…its units digit is 0.
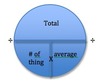
Quotient
the result of division
Divisor
the number you divide by
Numerator
the top number in a fraction
denominator
the bottom number in a fraction
Order of operations in solving a complex problem
PEMDAS (Please Excuse My Dear Aunt Sally): 1. parentheses 2. exponents 3. multiplication/division 4. addition/subtraction
1/100 = .? = ?%
0.01 = 1%
1/10 = .? = ?%
0.1 = 10%
1/5 = .? = ?%
0.2 = 20%
1/4 = .? = ?%
0.25 = 25%
1/3 = .? = ?%
0.333 = 33 1/3%
2/5 = .? = ?%
0.4 = 40%
1/2 = .? = ?%
0.5 = 50%
3/5 = .? = ?%
0.6 = 60%
2/3 = .? = ?%
0.666 = 66 2/3%
4/5 = .? = ?%
0.8 = 80%
3/4 = .? = ?%
0.75 = 75%
1/1 = ? = ?%
1.0 = 100%
2/1 = ? = ?%
2.0 = 200%
√2 =
1.4
√3 =
1.7
√4 =
2
Median
the middle value in a set of numbers
Mode
is the number or range of numbers in a set that occurs the most frequently: Mode = most
Range
is the difference between the highest and the lowest numbers in your set
The rates of normal distribution on a bell curve?
is 34:14:2
Factored form: x2 - y2
Unfactored form: (x+y)(x-y)
Factored form: (x+y)2
Unfactored form: x2 + 2xy + y2
Factored form: (x-y)2
Unfactored form: x2 - 2xy + y2
FOIL stands for…
first, outer, inner, last
To solve a permutation…
figure out how many slots you have, write down the number of options for each slot, and multiply them. Ex. 5X4x3 = 60
To solve a combination…
figure out how many slots you have, fill in the slots as you would a permutation, and then divide by the factorial of the number of slots.
Factorial: 6!
A factorial of a number is equal to that number times every positive whole number smaller than itself, down to 1: 6x5x4x3x2x1 = 720
Equation for finding probability
Average formula as pie chart
Rate formula
d=rt
avg speed = total distance ÷ time
Formula for percent change
Definition of terms: if you need to find the % increase, the “original” # will be the lower #. If you need to find the % decrease, the “original” # will be the higher #.
Line equation
y = mx + b
Slope equation
rise/run
Perimeter of a rectangle
the sum of the lengths of its four sides
Area of a rectangle
is the length times its width (lxW)
Diagonal of a square =
is 45:45:90
Perimeter of a square
four times the amount of one side
Each angle of an equilateral triangle =
60 degrees
Isosceles triangle
two of the three sides are equal in length
The longest side of a right triangle is called
the hypotenuse
Perimeter of a triangle
the sum of the lengths of the sides
the third-side rule
The length of any one side of a triangle must be less than the sum of the other two sides and greater than the difference between the other two sides
Area of a triangle
A = 1/2bh
Pythagorean theorem
only applies to right triangles
What are the three pythagorean triples?
3-4-5; 6-8-10; 5-12-13
What are the angles and the sides of a Isosceles right triangle?
angles: 45:45:90 sides: x:x:x√2
What are the sides of a 30:60:90 right triangle?
x:x√3:2x
Area of a square
any side squared
Formula for volume of a rectangular solid
lwh (length x width x height or depth)
Volume of a cylinder
πr²h
In y=mx+b, x and y stand for
points on the line
In y=mx+b, b stands for
y-intercept, or the point at which the line crosses the y-axis
In y=mx+b, m stands for
the slope of the line
The formula to find the length of a diagonal inside a three dimensional box
a2 + b2 + c2 = d2
The surface area of a rectangular box is equal to
the sum of the areas of all of its sides. Ex., a box whose dimensions are 2x3x4. Two sides of 2x3, two sides of 3x4, and two sides of 2x4. Thus, 6+6+12+12+8+8=52=surface area
Formula to find the radius of an area 49π
√49
The three types of assumptions for an argument essay. What are they and what are the keys to identifying them?
- Sampling Assumption: Look for a conclusion that generalizes from a small sample of evidence (e.g., 2 out of 5 dentists recommend….) 2. Analogy Assumption: assumes that the items being compared are the same. 3. Causal Assumption: these always assume that (1) if you remove the cause, you will remove the effect and (2) there is no other cause. Look for words like “causes,” “responsible for,” and “due to.”
⅛ = .? = ?%
0.125 = 12.5%
⅜ = .? = ?%
0.375 = 37.5%
⅝ = .? = ?%
0.625 = 62.5%
⅞ = .? = ?%
0.875 = 87.5%
Perimeter of a rectangle
sum of the lengths of its four sides
Area of a rectangle
l x w
Perimeter of a square
4 times the length of any side
The sum of the three angles of any triangle
180º
An equilateral triangle has…
three sides equal in length and three equal angles
The angles of an equilateral triangle are
60º each
