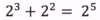Index Laws Flashcards
What is index notation for?
To write and manipulate long algebraic expressions, very big or very small numbers easily.
Name the parts of this expression:
The term being raised to a power is called the “base” and the power is the “index” or exponent.
How would you write the following in index notation?
How would you rewrite the following in index notation?
First Law of Indicies:
Anything raised to the power of zero is…?
Anything raised to the power of zero is
ONE
Second Law of Indices
A negative exponent means….
Negative exponents make you sad and “bring you down”, which means you put the term in the bottom of a fraction. Once you move the term to the denominator, the exponent is positive.
Expand:
What is…?
Rewrite with a positive exponent:
Note: the base stays exactly the same!
3rd Law of Indices
What happens when you multiply identical bases?
When you multiply identical bases, their indices add together.
Simplify:
Simplify into a single term:
Write with (the secret) exponent:
Rewrite as a negative exponent:
4th Law of Indices
What happens when you divide identical bases?
When you divide identical bases, the indices subtract: exponent from the top - exponent from the bottom:
What is….?
5th Law of Indices
What happens when an index is raised to the power of another index?
When an index is raised to the power of another index, they multiply together
What is…?
6th Law of Indices
What does a fractional index mean?
A fractional index is a RADICAL way of expressing a RADICAL
What is…?
How would you rewrite this without any index at all?
It is a bring-me-down-RADICAL combo!
How do you deal with a negative index that’s ALREADY in the bottom part of a fraction?
Negative exponents make me flip out! Flip the term to the other side of the fraction to make the index positive :)
Express in index notation:
Expand:
True or false?
True!! Negative exponents make me sad and “bring me down”, which means you put the term in the bottom of the fraction. The 3 in the y3 term is positive, so it stays where it is!
True or false?
True!! Radicals (like a square root) can be expressed as fractional indices. Notice that we don’t usually write the “2” for a square root. That’s where the 2 in the bottom part of the index comes from
True or false?
False! When you multiply identical bases together, you must ADD their indices.
True or false?
False! You can combine identical bases ONLY when you are multiplying or dividing them
True or false?
True! The y term inside the bracket has a (secret) index of 1. Both x2 and y are being raised to the power of 3. This index “distributes” with the indices inside the bracket (as long as everything inside the bracket is multiplied or divided).
True or false?
False! Only IDENTICAL bases can be combined, and their indices are added together. If the bases are different they CAN’T be combined.
