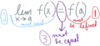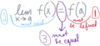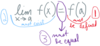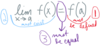June 8 and Later Flashcards by Brian Higginbotham

𝚫
means
_____.

How well did you know this?

Not at all

Perfectly

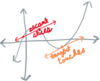
Average rate of change
is associated with
[tangent / secant].

secant

How well did you know this?

Not at all

Perfectly

Instantaneous rate of change
is associated with
[tangent / secant].

tangent

How well did you know this?

Not at all

Perfectly

Touching at one point
is associated with
[tangent / secant].

tangent

How well did you know this?

Not at all

Perfectly

Derivative
is associated with
[tangent / secant].

tangent

How well did you know this?

Not at all

Perfectly

𝚫f = f(x₂) − f(x₁)
𝚫x x₂ − x₁

is associated with
[ instantaneous rate of change /
average rate of change ].

average rate of change

How well did you know this?

Not at all

Perfectly

𝚫f = f(x₂) − f(x₁)
𝚫x x₂ − x₁

is associated with
[tangent / secant].

secant

How well did you know this?

Not at all

Perfectly

lim_𝚫_x→0 𝚫f
𝚫x

is associated with
[ instantaneous rate of change /
average rate of change ].

instantaneous rate of change

How well did you know this?

Not at all

Perfectly

df (x)
dx

is associated with
[ instantaneous rate of change /
average rate of change ].

instantaneous rate of change

How well did you know this?

Not at all

Perfectly

To talk about
instantaneous rate of change,
you must specify a
_____.

location

How well did you know this?

Not at all

Perfectly

To talk about
average rate of change,
you must specify an
_____.

interval

How well did you know this?

Not at all

Perfectly

How well did you know this?

Not at all

Perfectly

How well did you know this?

Not at all

Perfectly

How well did you know this?

Not at all

Perfectly

How well did you know this?

Not at all

Perfectly

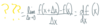
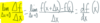
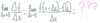
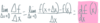
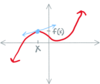
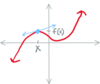
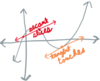
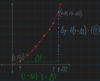
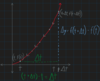
Envision a

*graph** of how the definition of
*derivative** works?

How well did you know this?

Not at all

Perfectly

The
equation for
average rate of change is below.

How does it relate to the
equation for
instantaneous rate of change?

How well did you know this?

Not at all

Perfectly

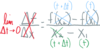
This

lim_𝚫x→0 f(x + 𝚫x) − f(x)
𝚫x

may be
described verbally as
“the limit of the
_____ of f(x) over the interval [x, x + 𝚫x] as
𝚫x→0.

average rate of change

How well did you know this?

Not at all

Perfectly

This

lim_𝚫x→0 f(x + 𝚫x) − f(x)
𝚫x

may be
described verbally as
“the limit of the
average rate of change of f(x) over
the interval
_____ as 𝚫x→0.

[x, x + 𝚫x]

How well did you know this?

Not at all

Perfectly

To
evaluate a limit,

i.e.
lim_x→1 √(x² + 4) − 2
x²

*first**
*_____**.

plug in the limit point value

(here, x = 1)

How well did you know this?

Not at all

Perfectly

In
evaluating a limit,

i.e.
lim_x→1 √(x² + 4) − 2
x²

if you
plug in the
_____
and get a
well-defined result,
that’s the limit.

limit point value

How well did you know this?

Not at all

Perfectly

In
evaluating a limit,

i.e.
lim_x→1 √(x² + 4) − 2
x²

if you
plug in the
limit point value
and get a
_____,
that’s the limit.

well-defined result

How well did you know this?

Not at all

Perfectly

How would you write this

lim_𝚫x→0 f(x + 𝚫x) − f(x)
𝚫x

in
Leibniz notation?

df (x)
dx

How well did you know this?

Not at all

Perfectly

How would you write this

lim_𝚫x→0 f(x + 𝚫x) − f(x)
𝚫x

in
prime notation?

f’(x)

How well did you know this?

Not at all

Perfectly

This **f'(x)** is written in [_Leibniz / prime_] notation.

**prime**

This **_df_ (x) dx** is written in [_Leibniz / prime_] notation.

**Leibniz**

_First Primary Interpretation of the Derivative_ (analytical): f'(x) is the * *\_\_\_\_\_** of f(x) at the * *value x** ( or at (x, f(x))

**instantaneous rate of change**

_Second Primary Interpretation of the Derivative_ (geometric): f'(x) is the * *\_\_\_\_\_** of the line * *tangent** to the graph of f(x) at the point * *(x, f(x))**

**slope**

_f(x) is a function_. Its derivative, **_df_ dx** = **lim_𝚫x→0 _𝚫f_ 𝚫x** **= f'(x)** * *=** **lim_𝚫x→0 _f(x +_** _𝚫x) **− f(x)**_ * *𝚫x** is **\_\_\_\_\_** function.

**another**

What happens if you * *immediately** use the * *plug-in rule** for limits on a * *derivative**?

You get **0/0.**

With derivatives, **\_\_\_\_\_** is called **indeterminate form**, meaning that there's **not enough information** to determine whether **the limit exists**.

**0/0**

With derivatives, **0/0** is called **\_\_\_\_\_**, meaning that there's **not enough information** to determine whether **the limit exists**.

**indeterminate form**

With derivatives, **0/0** is called **indeterminate form**, meaning that there's **\_\_\_\_\_** to determine whether **the limit exists**.

**not enough information**

With derivatives, **0/0** is called **indeterminate form**, meaning that there's **not enough information** to determine whether **\_\_\_\_\_**.

**the limit exists**

**\_\_\_\_\_** is built into the **definition** of the **derivative**.

**Indeterminate form**

To find the * *slope** of a line * *tangent** to points on this function, f(x) = 2x³ − 6x² + x + 3, you \_\_\_\_\_.

**differentiate it**. f'(x) = 6x² − 12x + 1.

There is a line * *tangent** to this function at the point * *(−0.5, 0.75)**. The **slope** of line at that point is **8.5**. What is an **equation** for that tangent line?

**y − 0.75 = 8.5(x + 0.5)**

What is the **point−slope form** of a line?

**y − y₀ = m(x − x₀)**

A * *function** f(x) is * *\_\_\_\_\_** at x = a if * *lim_x→a f(x) = f(a).**

**continuous**

A * *function** f(x) is * *continuous** at x = a if * *\_\_\_\_\_ = f(a).**

**lim_x→a f(x)**

A * *function** f(x) is * *continuous** at x = a if * *lim_x→a f(x) _____ f(a).**

**=**

A * *function** f(x) is * *continuous** at x = a if * *lim_x→a f(x) = \_\_\_\_\_.**

**f(a)**

Is this function * *continuous** at * *x = a**? If not, **why not**?

* *No:** * *lim_x→a f(x) ≠ f(a)**.

Is this function * *continuous** at * *x = a**? If not, **why not**?

* *No:** * *f(a) is undefined**.

Is this function * *continuous** at * *x = a**? If not, **why not**?

* *No:** * *lim_x→a f(x) DNE**.

"**Continuity** is a **\_\_\_\_\_** concept."

**point-by-point**

A function f(x) is called * *continuous** if it's * *continuous** at every * *\_\_\_\_\_**.

**x ∈ D**

**f(x) = _1_ , x ≠ 0 x** ``` Is f(x) **continuous** at x = 0? ```

**Yes**: x = 0 is not in the domain of this function, so it's technically continuous.

**f(x) = _1_ x** ``` Is f(x) **continuous**? ```

**No**: f(x) is not continuous at x = 0.

What is a * *math term** for * *plugging this hole**?

**continuously extending**

How might you **continuously extend** f(x)?

**Redefine it**:

**Continuously extending** a function turns it into a **\_\_\_\_\_**.

**piecewise function**

f_c(x) is the **\_\_\_\_\_** of f(x).

**continuous extension**

At a \_\_\_\_\_, a function is **continuous** if it is continuous in the **one-sided sense**.

**boundary point**

At a **boundary point**, a function is **continuous** if it is continuous in the **\_\_\_\_\_**.

**one-sided sense**

There are basically **two (related) definitions** of **continuity**: one for \_\_\_\_\_ and one for **interior points**.

**boundary points**

There are basically * *two (related) definitions** of * *continuity**: one for * *boundary points** and one for * *\_\_\_\_\_**.

**interior points**

**f(x) = _1_ , x ≠ 0 x** ``` Is f(x) **continuous**? ```

**Yes**: f(0) is not in its domain.

_Graphically_, how can you tell whether a **function** is **continuous**?

You can * *graph** it without lifting your * *stylus**.

A * *rational function** is continuous for * *\_\_\_\_\_**.

**x ∈ ℝ**, so long as the **denominator ≠ 0**.

A * *polynomial** is continuous for * *\_\_\_\_\_**.

**x ∈ ℝ**

Given that _f(x) and g(x)_ are _continuous_ at x = a, **f(x) ± g(x)** is \_\_\_\_\_ at x = a.

**continuous**

Given that _f(x) and g(x)_ are _continuous_ at x = a, **f(x) g(x)** is \_\_\_\_\_ at x = a.

**continuous**

Given that _f(x) and g(x)_ are _continuous_ at x = a and _k ∈ ℝ_, **k f(x)** is \_\_\_\_\_ at x = a.

**continuous**

Given that _f(x) and g(x)_ are _continuous_ at x = a, **_f(x)_ g(x)** is \_\_\_\_\_ at x = a.

**continuous** (provided g(x) ≠ 0)

The **difference** between the **two defintions of continuity** is whether you can use a **\_\_\_\_\_**.

**one-sided limit** | (boundary points only)

Given: _c(x) = o(i(x))_, according to the **\_\_\_\_\_**, c(x) is **continuous at x = a** if: * **lim_x→a i(x) = L exists** and * **o(x) is continuous** at * *lim_x→a i(x) = L**.

**continuity of function compositions theorem**

Given: _c(x) = o(i(x))_, according to the **continuity of function compositions theorem**, c(x) is **\_\_\_\_\_** if: * **lim_x→a i(x) = L exists** and * **o(x) is continuous** at * *lim_x→a i(x) = L**.

**continuous at x = a**

Given: _c(x) = o(i(x))_, according to the **continuity of function compositions theorem**, c(x) is **continuous at x = a** if: * **\_\_\_\_\_** and * **o(x) is continuous** at * *lim_x→a i(x) = L**.

**lim_x→a i(x) = L exists**

Given: _c(x) = o(i(x))_, according to the **continuity of function compositions theorem**, c(x) is **continuous at x = a** if: * **lim_x→a i(x) = L exists** and * **\_\_\_\_\_** at * *lim_x→a i(x) = L**.

**o(x) is continuous**

Given: _c(x) = o(i(x))_, according to the **continuity of function compositions theorem**, c(x) is **continuous at x = a** if: * **lim_x→a i(x) = L exists** and * **o(x) is continuous** at * *\_\_\_\_\_**.

**lim_x→a i(x) = L**

Given: _c(x) = o(i(x))_, for the **continuity of function compositions theorem** to apply at x = a, i(x) needs to **\_\_\_\_\_** at x = a, but not to **be continuous** at x = a.

**have a limit**

Given: _c(x) = o(i(x))_, for the **continuity of function compositions theorem** to apply at x = a, i(x) needs to **have a limit** at x = a, but not to **\_\_\_\_\_** at x = a.

**be continuous**

_Best Practice_: When dealing with **inverse trig functions**, always **\_\_\_\_\_**.

**make a chart**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **\_\_\_\_\_** **f(x_min) = m** if there exists **x_min ∈ [b, d]** s.t. **f(x_min) = m _\<_ f(x)** for all **x ∈ [b, d]**.

**global minimum value**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **\_\_\_\_\_** **f(x_max) = M** if there exists **x_max ∈ [b, d****]** s.t. **f(x_max) = M** **_\>_** **f(x)** for all **x ∈ [b, d]**.

**global maximum value**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **global minimum value** **\_\_\_\_\_** if there exists **x_min ∈ [b, d]** s.t. **f(x_min) = m _\<_** **f(x)** for all **x ∈ [b, d]**.

**f(x_min) = m**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **global maximum value** **\_\_\_\_\_** if there exists **x_max ∈ [b, d]** s.t. **f(x_max) = M** **_\>_** **f(x)** for all **x ∈ [b, d]**.

**f(x_max) = M**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **global minimum value** **f(x_min) = m** if there exists **\_\_\_\_\_** s.t. **f(x_min) = m** **_\<_** **f(x)** for all **x ∈ [b, d]**.

**x_min ∈ [b, d]**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **global maximum value** **f(x_max) = M** if there exists **\_\_\_\_\_** s.t. **f(x_max) = M _\>_** **f(x)** for all **x ∈ [b, d]**.

**x_max ∈ [b, d]**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **global minimum value** **f(x_min) = M** if there exists **x_min ∈ [b, d]** s.t. **\_\_\_\_\_** for all **x ∈ [b, d]**.

**f(x_min) = M _\<_ f(x)**

According to the _extreme value theorem_, a function f(x) over x ∈ [b, d] has a **global maximum value** **f(x_max) = M** if there exists **x_max ∈ [b, d]** s.t. **f(x_max) = M _\>_ f(x)** for all **\_\_\_\_\_**.

**x ∈ [b, d]**

***Any* maximum or minimum** (local or global) of f(x) is called an **\_\_\_\_\_**.

**extreme value**

***\_\_\_\_\_*** (local or global) of f(x) is called an **extreme value**.

***Any* maximum or minimum**

Given _f(x) = x, x ∈ [0, 1)_, where does f(x) have a **global maximum**?

**n/a**

Given _f(x) = x, x ∈ [0, 1)_, where does f(x) have a **global minimum**?

**x = 0**

This function has **global max** [_x_max = 1/2 / y_max = 1/4_] at [_x_max = 1/2 / y_max = 1/4_].

**global max y_max = 1/4** **at x_max = 1/2**

This function has **global min y_min = 0** at \_\_\_\_\_.

**x_min = {0, 1}**

**[b, d]** is a **\_\_\_\_\_**, **bounded** domain.

**closed** | (b, d are *included*)

**[b, d]** is a **closed**, **\_\_\_\_\_** domain.

**bounded** | (b, d are *finite*)

f(x) is * *continuous** over * *[b, d].** It [_must / might / cannot_] have **global extremes**?

**must** f(x) is continuous over a closed and bounded domain, so it must have global extrema in that interval.

f(x) is * *not continuous** over * *[b, d]**. It [_must / might / cannot_] have **global extremes**?

**might** Continuity over a closed, bounded interval is _sufficient_ (per the EVT), but it is _not necessary_.

f(x) is * *continuous** over * *[b, d)**. It [_must / might / cannot_] have **global extremes**?

**might** f(x) is not known to be continuous over a closed and bounded domain, so the EVT doesn't apply.

According to the _intermediate value theorem_, suppose * f(x) is * *\_\_\_\_\_** over x ∈ [b, d], * **m = y_min** is the global minimum over [b, d], and * **M = y_max** is the global maximum over [b, d], then, for any * *y_int ∈ [m, M]**, there exists at least one value * *c ∈ [b, d****]** s.t. * *f(c) = y_int**.

**continuous**

According to the _intermediate value theorem_, suppose * f(x) is * *continuous** over x ∈ [b, d], * **m = y_min** is the global minimum over [b, d], and * **M = y_max** is the global maximum over [b, d], then, for any * *\_\_\_\_\_**, there exists at least one value * *c ∈ [b, d]** s.t. * *f(c) = y_int**.

**yint ∈ [m, M]**

According to the _intermediate value theorem_, suppose * f(x) is * *continuous** over x ∈ [b, d], * **m = y_min** is the global minimum over [b, d], and * **M = y_max** is the global maximum over [b, d], then, for any * *y_int ∈ [m, M]**, there exists at least one value * *\_\_\_\_\_** s.t. * *f(c) = y_int**.

**c ∈ [b, d]**

According to the _intermediate value theorem_, suppose * f(x) is * *continuous** over x ∈ [b, d], * **m = y_min** is the global minimum over [b, d], and * **M = y_max** is the global maximum over [b, d], then, for any * *y_int ∈ [m, M]**, there exists at least one value * *c ∈ [a, b]** s.t. * *\_\_\_\_\_**.

**f(c) = y_int**

_Visualize_ the **intermediate value theorem**:

How does the * *intermediate value theorem** relate to the * *extreme value theorem**?

The IVT **depends on** the EVT. The EVT tells us that if a function is continuous over a closed, bounded domain, there will be a global maximum and a global minimum. The IVT adds that, in that domain, the function will output every y-value between the global extrema at least once.

_Trick_: "With **square roots**, multiply the numerator and denominator by the **\_\_\_\_\_**."

**algebraic conjugate**