Lecture 2 - Current developments in DFT Flashcards
1
Q
- EXC is … and needs to be …
A
- EXC is unknown and needs to be approximated
2
Q
- What is the basic assumption of Local-density approximations (LDA)?
A
- EXC only depends on the value of the local electron density at one point
3
Q
- How does an ensemble generalized LDA approximate XC energy as a functional of electron density?
A
- Exactly calculates ϵXCHEG energy density for a homogenous electron gas (HEG)
4
Q
- What is a homogeneous electron gas?
A
- Box of homogeneous positive charge background filled with electrons (no atoms)
- These electrons spread out homogeneously allowing exact calculation depending on the density at that separation.
5
Q
- Discuss the structural, elastic and vibrational properties as a result of the use of LDAs
- what approximation yields these results
A
- Generally, give satisfactory results
- Crystal bulk lattice (distance of unit cell vector) more accurate as usually underestimated
- Bulk moduli (E to compress/expand solid) too large but 10% error not uncommon
- Vibrational frequencies too high/stiff
- These are due to local approximation which compacts the entire system.
6
Q
- Discuss some other problems with LDA’s
A
- Binding energies are too negative i.e.overbinding
- Activation energies are unreliable
- Band gaps, ionization energies and electron affinities are strongly underestimated.
7
Q
- What are Generalized-gradient approximation (GGA’s) and how do they improve upon LDAs
A
- Similar form but a local gradient of electron density is included as well as the value of density
- This is to gain information on the local variation in neighbouring electron density at other positions
8
Q
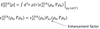
- What strategies can be taken in designing functionals
A
- Non-empirical functionals: satisfy constraints via certain known mathematical/physical boundary conditions (less accurate)
- Empirical functionals: satisfy a property by empirically fitting to yield prediction of a molecule/material property (more accurate – regularly used)
9
Q
- What is the disadvantage of empirical design of functionals?
A
- Are derived from QM with good accuracy, however, are not truly ab initio.
10
Q
- How does the bulk lattice constants and cohesive energies with GGA compare with LDA?
A
- Bulk lattice constants (unit cell vecotr between atoms): GGA increase due to more repulsive core-valence XC
- Cohesive energies (E released by binding atoms in to a solid): GGA reduction mostly due to valence effect, giving better description.
11
Q
- How do Energy barriers of GGAs compare to LDAs
A
- Free energy of molecule better described with GGAs, reducing the degree to which the barrier is underestimated
- LDAs underestimate to a large extent.
12
Q
Name an improvement GGAs make on LDAs
A
- GGA correct LDA overbinding, with less stiffness of tightly packed system
13
Q
- Where do GGAs still fall short
A
- Still no long-range description of vdW forces as local approximation (same as LDA)
- As GGA favours low coordination (large gradient), can now interpret different E sites on a surface (LDA could not distinguish). However can do so incorrectly.
14
Q
- For their simplicity, LDA/GGAs perform well for a large range of materials, marking ‘semi-…’ DFT as an important improvement in how we describe the …
- However major failures in the … of chemical reduction barriers and … … as well as the overestimation of … mark a need for further improvement.
A
- For their simplicity, LDA/GGAs perform well for a large range of materials, marking ‘semi-local’ DFT as an important improvement in how we describe the EXC
- However major failures in the underestimation of chemical reduction barriers and band gaps as well as the overestimation of polarizabilities mark a need for further improvement.
15
Q
- What is an example of a GGA functional?
A
- Perdew-Burke-Ernzerhof (PBE)
16
Q
- What is the general idea of meta-GGAs?
A
- Expand the local function dependence to occupied KS orbitals.
- 2nd derivative of KE added via T[ρ] of non-interacting electrons i.e. the product of the derivative of KS ψ of single particle space
- This leads to the function becoming explicitly orbital dependent.
- Still technically local derivative however accounts for many variations in different orbitals.
17
Q
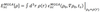
- How do meta-GGAs compare to LDA/GGA
A
- Better molecular binding E’s
- Better cohesive/structural description
- Band gaps still underestimated
- Long range vdW still not accounted for as still a local functional
18
Q
(IMP) Describe the band-gap problem in GGA’s
A
- Underestimation of difference in ionisation energy/electron affinity due to self-interaction error
- Contrary to HF, VX and VH + VC don’t cancel for an H-atom
- Missing VX causes half electrons to move apart from each other instead of contracting in to a positive and negative ion in dissociation.
19
Q
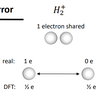
(IMP) What is the over localisation error also associated with the band gap problem?
A
- Electronic states are too localised as electrons do not sufficiently repel each other (Pauli repulsion missing)
- Electrons do not come close in contact unless they must (run away from themselves as orbitals more diffuse.
20
Q
(IMP) Describe the problem of missing long-range correlation in local functionals
A
- Electron correlation VC treated incorrectly (due to local approximation)
- Leading to no long range interaction between non overlapping densities
- As a result, LDA/GGA/meta-GGA do not capture dispersion/vdW effects
21
Q
(IMP) How does the error in delocalization affect how the ionisation energy and electron affinity are related to the energies of the KS states at this stage? Use a sketch to support your answer
A
- Energies of the KS auxiliary states do not equal the electron affinity and ionisation energy of the system as they should
- This is due to the presence of half electrons in local description causing a bowing of the curve instead of clear definition
- means half an electron in LUMO and HOMO instead of 1 in LUMO (I underest, A overest, E underest)
- Gradient represents energy levels and are incorrect
22
Q
(IMP) What is the solution to the long-range correlation error?
A
Include explicit non-local correlation or long-range dispersion terms, describing sum of all pairwise interactions as a function as 1/r^6 e.g. Many body dispersion/ vdWsurf
23
Q
- What is an example of a meta-GGA
A
- TPSS
24
Q
(IMP) How do 4th-rung hybrid functionals solve the localization problem in meta-GGAs? Use a sketch to support your answer
A
- Includes HF exchange, which strongly over localizes/stabilizes electrons, making graph more convex.
25
* Give 2 examples of hybrid functionals
* B3LYP: most used xc, empirical mix of 3 functionals and HF exchange
* HSE06: PBE with 25% HF exchange at short range and PBE in the long range (range separated functional).
26
* How do hybrid functionals compare to local?
* Large improvements in barriers, band gaps and dissociation energies (≈0.1 eV expt)
* More accurate and consistent description of CO site adsorption.
27
* What is the idea of 5th rung RPA (Random Phase Approximation) functionals?
* Xc functionals become explicitly dependent on unoccupied orbitals as well as occupied orbitals previously
* Similar to CCSD in HF (mixing excitation to unoccupied states)
28
* How is the use of RPAs carried out?
* Ec is described via non-local dynamic correlation response functions allowing electrons to interact more
* Calculated via many body perturbation theory
29
* What is the Jacobs ladder of DFT? commment on its use in functional selection
* Form of finding a systematic relationship between functional approximations
* However not a truly systematic improvement process like we do in improving a wavefunction
* Therefore, can worse by moving up ladder, must be careful
30
31
One important numerical factor in PBC material simulations is Brillouin zone/k gird sampling, why do we do k grid sampling, and to what degree to ensure high enough accuracy(?)
Periodic systems are **translational invariant**, Blocks theorem tells us that **translation symmetry operator commutes with the Hamiltonian**, thereby every single wavefunction must be an eigenfunction of the translation operator, this is done with a **plane wave product**
32
