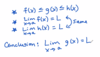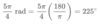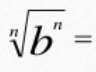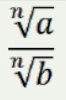MATH 112 Exam 1 Memorization

Question 1

(a/b)^x =

Answer 1

a^x/b^x

Question 2

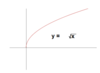
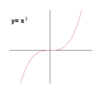
Domain and range of y = x³

Answer 2

• Domain: (-infinity, infinity)
• Range: (-infinity, infinity)

Question 3

What is one important prerequisite for a function to have an inverse function?

Answer 3

ONE-TO-ONE

(i.e., only one x-value for each y-value)

Question 4

Intermediate Value Theorem

Answer 4

The intermediate value theorem states that if f is a continuous function whose domain contains the interval [a, b], then it takes on any given value between f(a) and f(b) at some point within the interval.

Question 5

Domain and range of y = mx + b

Answer 5

• Domain: (-infinity, infinity)
• Range: (-infinity, infinity)

Question 6

When x < 0

1/x =

Answer 6

• sqrt 1/x²

Question 7

When is it no helpful to multiply by the radical conjugate when evaluating limits?

Answer 7

When you are evaluating limits at infinity. Instead, you should divide by 1/x^a where “a” is the greatest factor.

Question 8

Answer 8

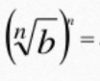
b

Question 9

Answer 9

Question 10

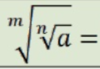
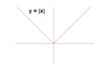
Domain and range of y = lxl

Answer 10

• Domain: (-infinity, infinity)
• Range: [0, infinity)

Question 11

Log Base conversion:

log_a x =

Answer 11

(log_b x) / (log_b a)

Question 12

Definition of Continuity

Answer 12

• f(x) is continuous at x = a
• limit as x approaches a of f(x) exists (this means
• left limit must exist, right limit must exist, and they must be equal
• f(a) exists (i.e., a is in the domain; i.e., there is a y-value for it; i.e., it is defined)

In short, the limit as x approaches a for f(x) = f(a) – [and they both exist]

Question 13

log_a (m) - log_a (n) =

Answer 13

log_a (m/n)

Question 14

a^x • a^y =

Answer 14

a^x+y

Question 15

sin(2x) = ?

Answer 15

2 sin x cos x

Question 16

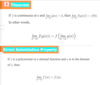
Limit Laws (and when they are true)

Answer 16

These laws do NOT apply when the limits do not exist! This includes when the limits are INFINITE! Infinite limits do not “exist”!!

Question 17

tan(-x) = ?

Answer 17

tan x

Question 18

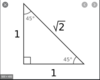
45-45-90 Triangle

Answer 18

Question 19

(when b<0 and n is even)

Answer 19

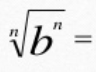
|b|

Question 20

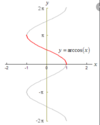
Domain and range of arctan x

Answer 20

• Domain: (-infinity, infinity)
• Range: (-π/2, π/2)

Question 21

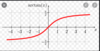
How to convert degrees to radians.

Answer 21

Question 22

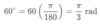
log_a (m) + log_a (n) =

Answer 22

log_a (mn)

Question 23

Answer 23

Question 24

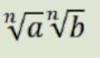
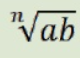
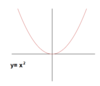
Domain and range of y = x²

Answer 24

• Domain: (-infinity, infinity)
• Range: [0, infinity)

Question 25

When does the direct substitution property apply?

Answer 25

When a function is continuous!

Question 26

Squeeze Theorem

Answer 26

NOTE: The functions do NOT have to be continuous!

Question 27

How to convert radians to degrees

Answer 27

Question 28

Domain and range of tan x

Answer 28

• Domain: π/2 + πn for all integers n
• Range: (-infinity, infinity)

Question 29

y = b^x when b < 1

Answer 29

Question 30

Domain and range of arccos x

Answer 30

• Domain: [-1, 1]
• Range: [0, π]

Question 31

y = b^x when b < 0

Answer 31

b CANNOT BE NEGATIVE

Question 32

Things you can’t do with radicals…

Answer 32

Question 33

Do infinite limits “exist?”

Answer 33

NO!!!!!

Question 34

sin² x + cos² x = ?

Answer 34

1

Question 35

(when b is non-zero and n>1)

Answer 35

b

Question 36

cos(-x) = ?

Answer 36

cos x

Question 37

Domain and range of y = 1/x

Answer 37

• Domain: (-infinity, 0) U (0, infinity)
• Range: (-infinity, 0) U (0, infinity)

Question 38

sin(-x) = ?

Answer 38

• sin x

Question 39

log_a (a) =

Answer 39

1

Question 40

Domain and range of cos x

Answer 40

• Domain: (-infinity, infinity)
• Range: [-1, 1]

Question 41

Domain and range of sin x

Answer 41

• Domain: (-infinity, infinity)
• Range: [-1, 1]

Question 42

Domain and range of y = e^x

Answer 42

• Domain: (-infinity, infinity)
• Range: (0, infinity)

Question 43

(a²b)³ =

Answer 43

a⁶b³

Question 44

Domain and range of y = sqrt x

Answer 44

• Domain: [0, infinity)
• Range: [0, infinity)

Question 45

log_a (1) =

Answer 45

0

Question 46

Answer 46

Question 47

log_a (m)ⁿ =

Answer 47

n log_a (m)

Question 48

y = b^x when b > 1

Answer 48

Question 49

n log_a (m) =

Answer 49

log_a (m)ⁿ

Question 50

Which functions are continuous on their domains?

Answer 50

Question 51

Domain and range of ln x or log x

Answer 51

• Domain: (0, infinity)
• Range: (-infinity, infinity)

Question 52

a^-x =

Answer 52

1/a^x

Question 53

Which functions have horizontal asymptotes (and where are they)?

Answer 53

• 1/x has H.A. at y = 0
• e^x has H.A. at y = 0
• arctan x has H.A. at y = -pi/2 and y = pi/2

Question 54

10^{log x} =

Answer 54

x

Question 55

When x > 0

1/x = ?

Answer 55

sqrt 1/x²

Question 56

30-60-90 Triangle

Answer 56

Question 57

Domain and range of arcsin x

Answer 57

• Domain: [-1, 1]
• Range: [-π/2, π/2]

Question 58

(a^x)^y =

Answer 58

a^xy

Question 59

a^x / a^y =

Answer 59

a^x-y