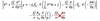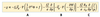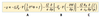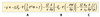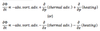mid term MEMORIZING Flashcards
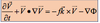
vector form of horizontal momentum equation in (x,y,p) coordinate system
Thus the forcing of the ageostrophic wind can be divided conveniently into the two parts,
the isallobaric wind and the advective wind.
geopotential tendancy
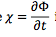
From the above (15) it follows that the isallobaric wind is determined by
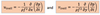
the gradient of the isolines of do p/do t
the isallobaric wind is determined by the gradient of the isolines of do p/ do t
these are
the lines connecting the equal amounts of surface pressure change (isallobars)
at point a
at point b
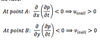
The direction of the isallobaric wind is perpendicular to
the isallobars
The direction of the isallobaric wind is perpendicular to the isallobars, always pointing towards the
falling pressure
The direction of the isallobaric wind is perpendicular to the isallobars, always pointing towards the falling pressure (i.e., pointing to the
minimum value where the strongest pressure decrease) in surface pressure is located.
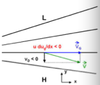
the advective wind arises when the
geostrophic wind is not uniform, as in diffluent or confluent flow pattern.
In diffluent flow pattern (fig), the geostrophic wind decreases
in positive x-direction
in diffluent flow pattern (fig), the geostrophic wind decreases in positive x-direction due to
the larger spacing between the isobars indicating smaller pressure gradient.
as u > 0
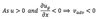
in this case the wind speed will
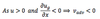
decrease
In the analogous case of a confluent flow the wind speed will
increase
When heights are falling the isobaric wind is
convergent
when hights are rising the isallobaric wind is
divergent
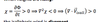
When there is Positive Vorticity Advection (PVA) the advective wind is
divergent
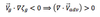
When there is Negative Vorticity Advection (NVA) the advective wind is
convergent
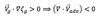
static stability parameter
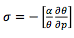
static stability parameter is a positive number for a
stable atmosphere
the equation states that
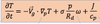
temperature change at a particular location and height is a function of temperature advection by geostrophic wind and vertical motion.
temperature advection relationship
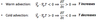
vertical motion relationship
because in a hydrostatic atmosphere do o| /do p is proportional to
the temperature (T) of the layer
the last term disapears because
if we assume that the static stability parameter is constant with height, the last term disappears
For a sinusoidal disturbance having a zero mean value, the horizontal
Laplacian of a field is proportional to
the negative of the field
the first term represents
the advection of absolute vorticity by the geostrophic wind.
the advection of absolute vorticity by the geostrophic wind relationships
term B is proportional to
the vertical derivative of temperature advection
the vertical derivative of temperature advection relationship
Strong CA over weak CA has the same effect asweak WA over strong WA
weak WA over strong WA
the third term represents
which behave similarly to
the differential heating term
the differential thermal advection term
The differential heating term relationship
Another useful way of writing the essence of the Q-G tendency equation is in qualitative form, as:
Thus, in quasi-geostrophic theory, there are only three ways for heights to fall. These are through:
- Positive Vorticity Advection or
- WA that increases with height or
- Diabatic heating that increases with height
Le Chatelier’s Principle, states that
states that many natural systems will resist changes, and if forced to change, will react with process that try to restore the original state.
We can see Le Chatelier’s principle at work in the
differential thermal advection and diabatic heating terms of the Q-G tendency equation.
these height rises and falls indicate that there must be a change in the vorticity at these levels
- increased vorticity where there are height falls, and
- decreased vorticity where there are height rises
To accomplish this vorticity change in a quasi-geostrophic framework, there must be
convergence where there are height falls, and divergence where there are height rises.
The convergence/divergence pattern leads to:
- upward motion and adiabatic cooling in the lower levels, and
- subsidence and adiabatic warming in the upper levels.
The adiabatic heating/cooling thus, opposes the
original temperature change due to advection.
