Number Properties Flashcards
(28 cards)
Is 0 odd or even?
Is 0 positive or negative?
0 is even.
0 is neither positive or negative. Problems often use the phrase “positive integers”– read carefully and realize they are talking about 1, 2, 3…. etc
What is 5 - (9 - x) ?
-4 + x
Be sure to distribute the - sign!
The double negative becomes a positive
5 - 9 + x
If xy < 0 , what can we conclude about x and y?
x and y have opposite signs:
one is positive, one is negative
If xyz > 0 , what can we conclude about x, y and z?
All 3 can be positive, OR there are 2 negatives and 1 positive
If y is an integer, what determines whether (-2)y is positive or negative?
If y is even, (-2)y is positive
If y is odd, (-2)y is negative
e.g. (-2)4 = -2 * -2 * -2 * -2 = 16
(each pair of negative signs cancels each other out)
(-2)5 = (-2)4 * -2 = 16 * -2 = -32
(there is 1 negative sign left without a pair)
What is (-2)3 * 1/2 * -3 * -1/2
-6
First, determine whether it’s positive or negative
There are an ODD # of negative signs, so it will be negative.
-8 * 1/2 * -3 * -1/2 = -6
If xy < 0, what can we conclude about x and y?
x must be negative
y can be positive or negative but can’t be an even integer
(-2)3 = -8
(-2)-3 = -1/8
(-2)4 = 16


If x is an integer, what can we conclude about 2x?
2x must be even
even * any integer = even

If b is odd, which must be even? E: 2b + 2
A) 2b - 3 –> 2b is even –> even - odd = odd
B) (b-1) / 2 –> even / 2 = even?
If b is a multiple of 4, yes. If not, no. (4/2 = 2 , 6/2 = 3)
C) b/2 must be a fraction, since odd means NOT a multiple of 2 (3/2 = 1.5)
D) odd*odd + even = odd + even = odd
E) even + even = even
What are the first 10 prime numbers?
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
If x is divisible by y, how can we write that?
x / y = Integer
x = y * Integer
We can also say that y is a Factor of x,
and x is a Multiple of y
How do you tell if an integer is divisible by 2?
by 3?
by 4?
by 5?
by 6?
by 8?
by 10?
2: It’s even
3: The sum of the digits is a multiple of 3
4: Divisible by 2 twice, or the last 2 digits are divisible by 4
5: ends in 0 or 5
6: Divisible by both 2 and 3
8: Divisible by two 3 times, or the last 3 digits are divisible by 8
10: ends in 0

If x/2 is even, what can we conclude about x?
X must be a multiple of 4
“Even” means a multiple of 2
x/2 = even
x = 2 * even
x = multiple of 4
Do the following have the same meaning? Or are any of them different?
a. 3 is a factor of 12
b. 3 is a divisor of 12
c. 12 is a multiple of 3
d. 12 is divisible by 3
e. 12/3 is an integer
f. 12 is equal to 3n, where n is an integer
g. 12/3 yields a remainder of 0
h. 12 items can be shared among 3 people so that each person has the same number of items
Yes, they all have the same meaning!
The GMAT often writes questions in different ways to confuse you.
It’s important to be able to translate the language into something you understand.
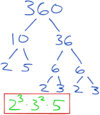
What is the Least Common Multiple of 18 and 24?
We factor each number and then find the “unique factors” – we find the highest power of each different prime factor and then multiply them.
18 = 3<strong>2</strong> * 2
24 = 23 * 3
The Least Common Multiple is 32 * 22 = 72
We can confirm this by writing out the multiples:
18: 18, 36, 54, 72
24: 24, 48, 72


1) If the units digit of N is 0, what do we know about the factors of N?
1) The factors include 2 and 5, because N must be a multiple of 10.
(For any number we want to factor that ends in one or more 0’s, it is easiest to factor the 10’s out first)
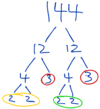
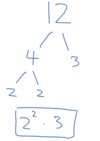
What is the prime factorization of 360?
(Draw a factor tree and then write the exponents)
Example:
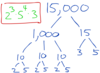
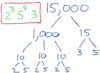
If the integer N ends with “5000”, what do we know about the factors of N?
From the 3 zeros at the end, the factors include 3 pairs of 2’s and 5’s, because N is a multiple of 1000.
Once we factor out 1000, we know that there is another 5 as a factor, since N/1000 would end with a 5.
Factors include 23 * 54
The image below shows an example of 15,000:
What is the remainder for 75/8?
What is 75/8 as a mixed number?
Remainder is 3. 9 3 /8
The remainder is the number left over after it is divided evenly.
If there were 75 cookies divided evenly among 8 people, each person would get 9, with 3 left over.
The 3 left over is 3/8 for each person.

When positive integer x is divided by positive integer y, the remainder is 2.
If x/y = 6.4, what is y?
5
Translate 1st sentence: x/y = integer + 2/y
x/y = 6 + .4
The decimal .4 is equivalent to the Remainder / y
.4 = 2/y
y = 2/.4 = 5
e.g. x = 32 cookies divided by y = 5 people
x/y = 32/5 = 6.4 = 6 each with 2 left over (remainder of 2)
2/y represents the 2/5 of a cookie for each person left over
If x is the product of the integers from 1 to 10, inclusive, what is the greatest integer n for which 2n is a factor of x?
8
We can represent x as 10! (10 Factorial)
x = 10! = 10*9*8*7*6*5*4*3*2
The question boils down to “How many 2’s are in the prime factorization of x?”
Only the even numbers have 2’s as factors:
2 has 1
4 has 2 (22)
6 has 1 (2*3)
8 has 3 2’s (23)
10 has 1 (2*5)
Add up all the 2’s: 1+2+1+3+1 = 8