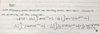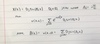PDE's Flashcards
Represent the PDE dtu - (dxxu + dyyu) + u3 - u = 0 as a function F
F: R4 to R, F(u, dtu, dxxu, dyyu)(x,y,t) = 0
Define linear and the order of a PDE
A PDE is linear if the associated function F is linear. The oreder of the PDE is the order of the highest derivative appearing in the PDE
When is a PDE well-posed
When it has a unique solution which continuously depends on data:
well-posedness = existence + uniqueness + stability
State the transport equation
dtu(x,t) + v(x,t)dx(u,t) = 0 for a function u where v(x,t) is a given function and we seek a solution in a time interval t in [0,T] with T in (0, inf) and x in R
State the characteristic method for solving the transport equation
With initial conditions u0: R to R s.t u(x0,0) = u0(x0), how do we solve the transport equation
How do we solve the transport equation now equal to a source term s(x,t, u(x,t))
State the wave equation
dttu - c2dxxu = 0
Derive the general solution to the wave equation
State the initial value problem for the wave equation in 1D
state D’Alembert’s formula
State Leibniz’s rule
Theorem: Show that the solution to the initial value problem wave equation is unique and given by D’Alembert’s formula
If we have the wave equation on a finite domain ie x in (0,L), how do we rescale the problem
State the homogeneous Dirichlet boundary conditions and the general solution
State the homogenous Neumann boundary conditions for the wave equation and the general solution
What are trigonometric polynomials of the degree 2n, give the complex and real versions
Given a fourier series exists, what are it’s coefficients?
State Bessel’s inequality
State Parseval’s equality and the conditions for it to hold
State the Riemann-Lebesgue lemma
When is a function odd and even
Let phi: R to R be 2pi periodic. If phi is even what is it’s fourier series? Likewise for odd
Let f, fn map [-pi, pi] to C. Define fn converging to f
i) pointwise
ii) uniformly
iii) mean square sense
Define the Dirichlet kernel and state its maximum
What is Sn(phi)(x) in terms of the Dirichlet kernel
State the initial boundary value problem for the heat equation in 1D with homogeneous dirichlet boundary conditions
Define the space-time rectangle and the parabolic boundary
State the maximum principle for the heat equation
Prove the maximum principle for the heat equation
State the initial boundary value problem for the heat equation in 1D with neumann boundary conditions
Show uniqueness for the heat equation using energy methods
How do we solve this problem?
State and prove Duhamel’s principle
What is the Cauchy problem for the heat equation
Whats the fundamental solution for the Cauchy problem
When is a PDE
i) elliptic
ii) hyperbolic
iii) parabolic
Define the Laplacian
State poissons equation
What is the laplacian in polar co-ordinates
State the wedge problem and its solution
When is u harmonic
When -(laplacian)u = 0
If f is in C2(Rn) and has a compact support, what equation u(x) solves -(laplacian)u = f on Rn
