Python Flashcards
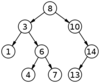
Example O(log n)
Binary search
Example O(n)
- Simple search
Example O(n * log n)
quicksort (fast)
Example O(n2)
- selection sort (slow)
actually O(n × 1/2 × n) list get's smaller each time you find an element
O(n!)
traveling salesperson
Explain O(n)
Big O and n = number of operations
time factor would be c*O(n)
Average cost for execution
binary search algo
- sorted list (!)
- calc mid point
- == return pos
- list[mid]> item -> high=mid-1
- list[mid]< item -> low=mid+1
def binary_search(list, item):
low = 0
high = len(list)-1
while low <= high:
delta=(high-low)//2
mid = low+delta
if list[mid] == item:
return mid
if list[mid] > item:
high = mid - 1
else:
low = mid + 1
return low
log 8
3: 23
log 1,024
10: 210
log 256
- 8: 28
Big O of reading array
O(1)
a[5]
Big O of reading linked list
O(n)
Big O of inserting array
O(n)
array with 4 elements and you add another requires new array and moving elements over
Big O of inserting linked list
O(1)
Minimal implementation of linked list
class Node: def \_\_init\_\_(self, **val=None**): self.val = val # the value self.next = None # reference to next node
find smallest element in array
def findSmallestIndex(arr): smallest\_index = 0 for i in range(1, len(arr)): if arr[i] \< arr[smallest\_index]: smallest\_index = i return smallest\_index
Selection sort
def selectionSort(arr): n=len(arr) for i in range(n): nmin=arr[i] npos=i for j in range(i+1,n): if arr[j]: **nmin=arr[j]** **npos=j** arr[npos]=arr[i] arr[i]=nmin
in-place sorting
Remove element from array\list
and return the value
- val=array.pop(index)
- from end arr.pop()
- from start arr.pop(0)
Count down using recursion
def countdown(i): print(i)
base case
if i <= 0:
return
else:
# recursion
countdown(i-1)
Runtime O(n)
Explain call stack
stack:
push new item on top
pop from the top most item
When you call a function from another function, the calling function is paused in a partially completed state.
Applies to recusrsion.
Library to import type List?
from typing import List
others:
from typing import Mapping, Optional, Sequence, Union
Library to import Optional?
- from typing import Optional
Get Maximum, Minimum
max() and min() no import required
Mutable vs immutable
mutable = liable to change
Everything in Python is an Object, every variable holds an object instance.
Objects of built-in types like (int, float, bool, str, tuple, unicode) are immutable.
Array slicing: from start index to end index?
arr[2:4]
Array slicing: from start index to end?
arr[3:]
a=[0,1,2,3,4,5,6]
a[3:]
Array slicing: from start to end index?
arr[:4]
ans = [0, 1, 2, 3]
Array slicing: negative index?
Counting from the end.
Array slicing: index with step?
print(list(range(0,13,3)))
[0, 3, 6, 9, 12]
Last index-1!
Array slicing: stepping entire array?
arr=list(range(0,13))
print(arr[::3])
Array slicing: reversing the array?
arr=list(range(0,13))
print(arr[::-1])
[12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
Array slicing: 2d array?
arr=[[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]]
arr[1][2:4]
ans = [8, 9]
Deque translation
Double Ended Queue
Main methods in deque
from collections import deque
d=deque([0,1,2,3,4,5])
append(item) and pop()
but also
appendleft()
popleft()
deque vs list
list: append and pop is O(n)
FIFO queue
first In, first Out
from queue import Queue
q=Queue(maxsize=10)
Methods:
qsize()
empty()
full()
put()
get()
LIFO
Last In, First Out - same as Stack
Python list:
arr. append(item)
arr. pop()
from queue import LifoQueue
from queue import LifoQueue
d=LifoQueue()
d.put(0)
d.put(1)
d.put(2)
d.put(3)
d.get() -> 3
Quick sort
- recursiv
- pivot
- generator for left and right
def quicksort(array):
if len(array) <=1: #empty or 1 element
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i <= pivot]
greater = [i for i in array[1:] if i > pivot]
return quicksort(less) + [pivot] + quicksort(greater)
Hash Function
“maps strings to numbers.”
What does a hash function do?
- The hash function consistently maps a name to the same index. Every time you put in “avocado”, you’ll get the same number back. So you can use it the first time to find where to store the price of an avocado, and then you can use it to find where you stored that price.
- The hash function maps different strings to different indexes. “Avocado” maps to index 4. “Milk” maps to index 0. Everything maps to a different slot in the array where you can store its price.
- The hash function knows how big your array is and only returns valid indexes. So if your array is 5 items, the hash function doesn’t return 100 … that wouldn’t be a valid index in the array
Creating a dictionary?
x={}
or
x=dict()
What is a a Palindrome?
- Number or word that spells the same forward and backwards.
- Can be odd and even
Anna
level
Binary Tree Traversals
Depth First Search (DFS):
Left always before right!
(a) Inorder (Left, Root, Right)
(b) Preorder (Root, Left, Right)
(c) Postorder (Left, Right, Root)
Breadth-First (BFS) or Level Order Traversal
Stack vs Heap
- Stack linear data structure
- Heap hierarchical data structure
- Stack never fragments
- Stack local variables
- Heap global variables
- Stack variables can’t be resized
- Heap variables can be resized
- Stack deallocation by compiler
- Heap done by programmer
- Stack is a linear data structure whereas Heap is a hierarchical data structure.
- Stack memory will never become fragmented whereas Heap memory can become fragmented as blocks of memory are first allocated and then freed.
- Stack accesses local variables only while Heap allows you to access variables globally.
- Stack variables can’t be resized whereas Heap variables can be resized.
- Stack memory is allocated in a contiguous block whereas Heap memory is allocated in any random order.
- Stack doesn’t require to de-allocate variables whereas in Heap de-allocation is needed.
- Stack allocation and deallocation are done by compiler instructions whereas Heap allocation and deallocation is done by the programmer.
BUD Principle
Bottlenecks
Unnecesssary Work
Duplicated work
Sort string
sorted(string)
Remove white spaces from string?
- strip(): returns a new string after removing any leading and trailing whitespaces including tabs (\t).
- rstrip(): returns a new string with trailing whitespace removed. It’s easier to remember as removing white spaces from “right” side of the string.
- lstrip(): returns a new string with leading whitespace removed, or removing whitespaces from the “left” side of the string.
Class stub
A Sample class with init method
class Person: def \_\_init\_\_(self, name): self.name = name
Create print() method in Class
def \_\_repr\_\_(self): return "Test()" def \_\_str\_\_(self): return "member of Test"
Linked list, delete middle node:
def delete_middle_node(node):
node. val=node.next.val
node. next = node.next.next
Base Methods for stack?
A stack is a last in - first out (LIFO) queue!
list methods: append, pop
LifoQueue methods: put, get, qsize, empty
Base methods for Queue?
- put
- get
- empty
- qsize
- full
Initialize:
from queue import Queue
q=Queue(5)
Inherit class, show constructor?
class Student(Person): def \_\_init\_\_(self, fname, lname): **super().\_\_init\_\_**(fname, lname)
How to override class methods?
- Use the same name for the method
class Parent(object): def \_\_init\_\_(self): self.value = 4 def **get\_value**(self): return self.value
class Child(Parent): def **get\_value**(self): return self.value + 1
Manually raise error
- raise Exception(‘I know Python!’)
- SyntaxError
- ValueError
- Warning
Tree definitions
Binary tree: each node has at most 2 children
A node is called a “leaf” node if it has no children.
Binary Tree vs. Binary Search Tree
- Binary Tree: Node, max 2 children
- Binary Search Tree (BST) = sorted binary tree
- BST: for each node left subtree < node < right subtree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure whose internal nodes each store a key greater than all the keys in the node’s left subtree and less than those in its right subtree.
Complete Binary Trees
A complete binary tree is a binary tree in which every level of the tree is fully filled, except for perhaps the last level.
To the extent that the last level is filled, it is filled left to right.
If there are not gpas then it would be Perfect Binary Tree.
Full Binary Tree?
- Each node has 0 = leaf or 2 children
A full binary tree is a binary tree in which every node has either zero or two children.
That is, no nodes have only one child.
Perfect Binary Trees
A perfect binary tree is one that is both full and complete.
All leaf nodes will be at the same level, and this level has the maximum number of nodes.
In-Order Traversal
def in_order_traversal(node:BinaryTree,level=0):
if node:
level+=1
in_order_traversal(node.left,level
print(‘ ‘*level+str(node.val))
in_order_traversal(node.right,level)
return
Pre-Order Traversal
def pre_order_traversal(node:BinaryTree,level=0):
if node:
level+=1
visit(node,level)
in_order_traversal(node.left,level)
in_order_traversal(node.right,level)
return
Post-Order Traversal
def post_order_traversal(node:BinaryTree,level=0):
if node:
level+=1
in_order_traversal(node.left,level)
in_order_traversal(node.right,level)
visit(node,level)
return
Binary Heaps
(Min-Heaps and Max-Heaps)
A min-heap is a complete binary tree (that is, totally filled other than the rightmost elements on the last level) where each node is smaller than its children.
Tries
(Prefix Trees)
- characters are stored in nodes
- use dictionary in python
- each level is a new dictionary
- ends with ‘*’
A trie is a variant of an n-ary tree in which characters are stored at each node. Each path down the tree may represent a word.
The * nodes (sometimes called “null nodes”) are often used to indicate complete words. For example, the
fact that there is a * node under MANY indicates that MANY is a complete word. The existence of the MA path
indicates there are words that start with MA.
O(k) with k = length of the word
same as hash
Graph
Graphs can be expressed as dictionaries = Adjacency List
d={}
d[nodex]=[nodey,nodez]
class **Graph()**: def \_\_init\_\_(self,val): self.val=val **self.children=[]**
Adjacency Matrices
An adjacency matrix is an NxN boolean matrix (where N is the number of nodes), where a true value at matrix[i][j] indicates an edge from node i to node j. (You can also use an integer matrix with Os and 1s.)
Bit operations in Python
print bin(123)
OperatorExampleMeaning
& a & b Bitwise AND
| a | b Bitwise OR
^ a^b Bitwise XOR (exclusive OR)
Only true if either is True- not both
~ ~a Bitwise NOT
« n Bitwise left shift - multiply by 2
» n Bitwise right shift - divide by 2^n-1
What does the following mean:
(( n & (n-1)) == 0)
Example: n is 15
then (n-1) = 14
n & (n-1) is only 0 if the two numbers dont share a bit.
-> this can only happen if n is 2^x
For example 2, 4, 8, 16, …
Singleton Class in Python
- __instance as class variable (no self)
- getInstance() as static method
- __init__ to allow setting __instance 1 time
class Singleton:
__instance = None
@staticmethod
def getInstance():
if Singleton.__instance == None:
Singleton()
return Singleton.__instance
def __init__(self):
if Singleton.__instance != None:
raise Exception(“This class is a singleton!”)
else:
Singleton.__instance = self
Memoization vs Recursion
A note on terminology: Some people call top-down dynamic programming “memoization” and
only use “dynamic programming“to refer to bottom-up work. We do not make such a distinction here. We call both dynamic programming.
Fibonacci number
- sum of previous 2 numbers
- starts with 0 and 1
In mathematics, the Fibonacci numbers, commonly denoted Fn, form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, …
Horizontal vs. Vertical Scaling
- Vertical scaling means increasing the resources of a specific node. For example, you might add additional memory to a server to improve its ability to handle load changes.
- Horizontal scaling means increasing the number of nodes. For example, you might add additional servers, thus decreasing the load on any one server.
Load Balancer
- distribute the load evenly
Typically, some frontend parts of a scalable website will be thrown behind a load balancer. This allows a system to distribute the load evenly so that one server doesn’t crash and take down the whole system. To do so, of course, you have to build out a network of cloned servers that all have essentially the same code and access to the same data.
Database Denormalization and NoSQL
- Table with redundant information.
Denormalization is one part of this. Denormalization means adding redundant information into a database to speed up reads.
Chr and Ord
Ord(‘A’)
and
Chr(2)
Modulo operator
%
Example: n % 26
What is a Tries (Prefix Trees)?
A trie is a variant of an n-ary tree in which characters are stored at each node. Each path down the tree may represent a word.
Runtime: O(k), with k the legth of the string
Min Heap
Algorithm Average Worst case
Space O(n) O(n)
Search O(n) O(n)
Insert O(1) O(log n)
Find-min O(1) O(1)
Delete-min O(log n) O(log n)
Max Heap
Algorithm Average Worst case
Space O(n) O(n)
Search O(n) O(n)
Insert O(1) O(log n)
Find-min O(1) O(1)
Delete-min O(log n) O(log n)
Find collision in Single Search
Find collision in Bidirectional Search
Binary Tree vs. Binary Search Tree?
all left descendents <= n < all right descendents
Binary Tree vs. Binary Search Tree?
all left descendents <= n < all right descendents
Complete Binary Trees?
A complete binary tree is a binary tree in which every level of the tree is fully filled, except for perhaps the last level. To the extent that the last level is filled, it is filled left to right.
Complete Binary Trees?
A complete binary tree is a binary tree in which every level of the tree is fully filled, except for perhaps the last level. To the extent that the last level is filled, it is filled left to right.
Full Binary Trees
A full binary tree is a binary tree in which every node has either zero or two children. That is, no nodes have only one child.
Full Binary Trees
A full binary tree is a binary tree in which every node has either zero or two children. That is, no nodes have only one child.
Perfect Binary Trees?
A perfect binary tree is one that is both full and complete. All leaf nodes will be at the same level, and this level has the maximum number of nodes.
Perfect Binary Trees?
A perfect binary tree is one that is both full and complete. All leaf nodes will be at the same level, and this level has the maximum number of nodes.
Dominos: There is an 8x8 chessboard in which two diagonally opposite corners have been cut off. You are given 31 dominos, and a single domino can cover exactly two squares. Can you use the 31 dominos to cover the entire board? Prove your answer (by providing an example or showing why it’s impossible).
- All dominos 8x8 = 64
- minus two diagonally opposite corners = 62
- Does Not work since we can’t place the 31 dominos
Jugs of Water: You have a five-quart jug, a three-quart jug, and an unlimited supply of water (but no measuring cups). How would you come up with exactly four quarts of water? Note that the jugs are oddly shaped, such that filling up exactly “half” of the jug would be impossible.
Easy:
- Fill 3
- Pour 3 into 5
- Fill 3
- Pour 3 until 5 is full -> left 1
- Toss 5
- Pour 1 quart in 5
- Fill 3
- Pour into 5
- Voila 4
The Apocalypse: In the new post-apocalyptic world, the world queen is desperately concerned about the birth rate. Therefore, she decrees that all families should ensure that they have one girl or else they face massive fines. If all families abide by this policy-that is, they have continue to have children until they have one girl, at which point they immediately stop-what will the gender ratio of the new generation be? (Assume that the odds of someone having a boy or a girl on any given pregnancy is equal.) Solve this out logically and then write a computer simulation of it.
Sequence:
G
BG
BBG
BBBG
Can sum probs for G:
0.5, 0.25, 0.125, ….
One way to think about this is to imagine that we put all the gender sequence of each family into one giant
string. So if family 1 has BG, family 2 has BBG, and family 3 has G, we would write BGBBGG
Rows and columns in Python
Matrix multiplication
- cols(A) * rows(B)
- result
