Reading 53 - Option Markets and Contracts

Question 1

What does a fiduciary call portfolio consist of?

Answer 1

• A long position in a European call option
• A long position in a pure-discount riskless bond

**gets its name because it is faithful to the notion of preserving capital**

Question 2

What does a protective put portfolio consist of?

Answer 2

• A long position in a European put option
• A long position in the underlying stock

Question 3

What is the formula for put-call parity for European options?

***Critical Concept****

Answer 3

Question 4

What is the general formula used to solve any “synthetic” options?

Answer 4

Question 5

What are the steps to creating a synthetic European call option?

Answer 5

• Buy a European put option on the same stock with the same exercise price (X) and the same maturity (T)
• Buying the stock
• Short the present value of X worth of a pure-discount riskless bond

Question 6

What are the steps to creating a synthetic European put option?

Answer 6

• Buying a European call option
• Shorting the stock
• Buying (i.e. investing in) the pure-discount riskless bond

Question 7

What are the steps to creating a synthetic stock position?

Answer 7

• Buy a European call option
• Short (i.e. writing) a European put option
• Buying ( i.e. investing in) the pure-discount riskless bond

Question 8

What are the steps to creating a synthetic pure-discount riskless bond?

Answer 8

• Buying a European put option
• Buying the stock
• Shorting (i.e. writing) a European call option

Question 9

A 1 yr call option on Cross Reef Inc. with an exercise price of $60 is trading for $8. The current stock price is $62. The risk-free rate is 4%. Calculate the price of the synthetic put option implied by put-call parity.

Answer 9

Question 10

What are 2 reasons why investors might want to create synthetic positions in securities?

Answer 10

1. To price options by using combinations of other instruments with known prices
2. To earn arbitrage profits by exploiting relative mispricing among the four securities. If put-call parity doesn’t hold, an arbitrage profit is available.

Question 11

What is the equation we use to calulate the the size of the Up (U) or Down (D) of the possible price changes in a binomial option model?

Answer 11

Either the U or D will be given. The equation to solve for the other is:

Question 12

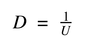
How do you calculate the risk-neutral probability of an up-move or down-move binomial option model?

***Critical Concept****

Answer 12

Question 13

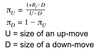
What are the 3 steps in calculating the value of an option on a stock?

Answer 13

1. Calculating the payoff of the option at maturity in both the up-move and down-move states
2. Calculating the expected values of the options in one year as the probability-weighted average of the payoffs in each state
3. Discounting the expected value back to today at the risk-free rate.

Question 14

Use the attached binomial tree to calculate the value today of a one-yr call option on the stock with an exercise price of $30. Assume the risk free rate is 7%, the current value of the stock is $30, and the size of an up-move is 1.333.

Answer 14

Question 15

How is an option’s delta calculated?

***Critical Concept***

Answer 15

Question 16

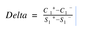
What are the steps in valuing an option using a two period binomial model?

***Critical Concept***

Answer 16

1. Calculate the stock values at the end of two periods
2. Calculate three possible option payoffs at the end of two periods
3. Calculate the expected option values at the end of two periods (t=2) using the up and down move probabilities
4. Discount the expected option values (t=2) back one period at the risk free rate to find the option values at the end of the first period (t=1).
5. Calculate the expected option value at the end of one period (t=1) using up and down probabilities
6. Discount the expected option value at the end of one period (t=1) back one period at the risk free rate to find the option value today.

Question 17

What are the 3 basic steps to valuing an option on a fixed income instrument using a binomial tree?

Answer 17

1. Price the bond at each node using the projected interest rates
2. Calculate the intrinsic value of the option at each node at the maturity of the option
3. Bring the terminal option values determined in step 2 back to today.

Question 18

How do you calculate the expiration value of a caplet of European style options???

**Critical Concept***

Answer 18

Question 19

How do you calculate the expiration value of a floorlet of European style options???

***Critical Concept***

Answer 19

Question 20

What are the 6 assumptions made in the Black-Scholes-Merton (BSM) model?

Answer 20

1. The price of the underlying asset follows a lognormal distribution
2. The (continuous) risk free rate is constant and known
3. The volality of the underlying aset is constant and known
4. Markets are “frictionless” (i.e. no taxes, transaction costs, limits to short selling)
5. The underlying asset has no cash flows
6. The options valued are European options.

Question 21

What are the 5 inputs to the BSM model?

***Critical Concept****

Answer 21

1. Asset price (Delta)
2. Exercise price
3. Asset price volatility (Vega)
4. Time to expiration (Theta)
5. The risk-free rate (Rho)

Question 22

What are the five sensitivity factors (“greeks”) of the BSM?

Answer 22

1. Delta
2. Gamma
3. Vega
4. Rho
5. Theta

Question 23

What does Delta measure?

Answer 23

It describes the relationship between asset price and option price.

* A call option’s delta is positive b/c as the underlying prices increases, so does the call options value

* A put option’s delta is negative b/c the put value falls as the asset price increases.

Question 24

What does Vega measure?

***Critical Concept****

Answer 24

It measures the sensitivity of the option price to changes in the volatility of returns on the underlying asset.

***Since calls and puts are more valuable the higher the volatility, vega is positive for puts and calls.

Question 25

What does Rho measure?

**Critical Concept***

Answer 25

It measures the sensitivity of the option price to changes in the risk free rate.

**Call option is positive

***Put option is negative

Question 26

What does Theta measure?

***Critical Concept***

Answer 26

It measures the sensitivity of the option price to the passage of time.

As time passes and a call option approaches maturity, its value declines, all else equal. aka “time decay”

Question 27

What does Gamma measure?

**Critical Concept***

Answer 27

How well the delta sensitivity measure will approximate the option price’s response to a change in the price of the underlying.

**Is larger when there is more uncertainty about whether the option will expire in or out of the money. This means gamma will tend to be large when the option is at-the-money and close to expiration

Question 28

During the last ten minutes of trading, call option on XYZ Inc common stock have risen from $1.20 to $1.60. Shares of the underlying stock have risen from $51.3 to $52.05 during the same time interval. Calculate the delta of the call option..

Answer 28

Question 29

What is the goal of delta-neutral portfolio (aka delta-neutral hedge) ?

Answer 29

To combine a long position in a stock with a short position in a call option so that the value of the portfolio does not change when the value of the stock changes.

Question 30

What is the formula to calculate the # of options needed to delta hedge?

**Critical Concept**

Answer 30

Question 31

What is a dynamic hedge (aka delta-neutral hedge)?

Answer 31

Since the delta neutral position only holds for very small changes in the value of the underlying stock. **B/c of this the portfolio must be continually rebalanced to maintain the hedge, **

Question 32

All else equal, does the existence of cash flows on the underlying asset increase or decrease the value of a call option?

Answer 32

Decrease

Question 33

All else equal, does the existence of cash flows on the underlying asset increase or decrease the value of a put option?

Answer 33

Increase

Question 34

What are the steps in computing historical volatility for use as an input in the BSM continuous-time options pricing model?

Answer 34

Question 35

What is Implied Volatility?

Answer 35

The value for standard deviation of continuously compounded rates of return that is “implied” by the market price of the option.

Question 36

A stock is priced at 40 and the periodic risk-free rate of interest is 8%. The value of a two-period European call option with a strike price of 37 on a share of stock using a binomial model with an up factor of 1.20 is closest to

Answer 36

First, calculate the probability of an up move or a down move:
U = 1.20 so D = 0.833

P<sub>u</sub> = (1 + 0.08 − 0.833) / (1.20 − 0.833) = 0.673 
P<sub>d</sub>= 1 − 0.673 = 0.327

Two up moves produce a stock price of 40 × 1.44 = 57.60 and a call value at the end of two periods of 20.60. An up and a down move leave the stock price unchanged at 40 and produce a call value of 3. Two down moves result in the option being out of the money. The value of the call option is discounted back one year and then discounted back again to today. The calculations are as follows:

C+ = [20.6(0.673) + 3(0.327)] / 1.08 = 13.745

C- = [3(0.673) + 0 (0.327)] / 1.08 = 1.869

Call value today = [13.745(0.673) + 1.869(0.327)] / 1.08 = 9.13

Question 37

Are American options worth more, less or the same the European options?

Answer 37

American options may be worth more but are never worth less than European options.

Question 38

How do interest rates levels affect call and put options?

Answer 38

When interest rates are higher

• Call option prices are higher
• Put option prices are lower

Question 39

How do you calculate the change in the option price if you have enough information to calculate the delta?

Answer 39

change in option price = Delta x Change in underlying price

Question 40

The risk free rate (Rho) is the continuously compounded rate on the risk free security whose maturity correspond’s to the option’s life.

If the discrete risk free rate quoted in annual terms is 5%, what the continuous rate?

Answer 40

r^c = ln(1+r)

r^c = ln(1.05)

r^c = 0.0488

r^c = 4.88%