Rules of Differentiation Flashcards
(31 cards)
1
Q

A

2
Q

A

3
Q
(csc x)1 =
A
-csc x cot x
4
Q
If f(x) is concave downwards over an interval, what does that tell you
A
f’(x) is decreasing
f’‘(x) is negative
5
Q
The derivative of the inverse of secant
A

6
Q
(ln x)1
A

7
Q
(cot x)1 =
A
-csc2x
8
Q
The derivative of the inverse of f(y)
A

9
Q
What is the chain rule
A

10
Q

A
= 0
11
Q
(cos x)1 =
A
-sin x
12
Q

A

13
Q

A

14
Q
If f(x) is concave upwards, what does that tell you
A
f’(x) is increasing
f’‘(x) is positive
15
Q
(logax)1
A

16
Q

A

17
Q
The derivative of arctan
A

18
Q
What is the slope of the normal line?
A
The negative reciprocal of the tangent line
19
Q

A
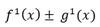
20
Q

A
1
21
Q
The derivative of arcsin
A

22
Q
What is the Extreme Value Theorem?
A
If f contains [a,b] and is continuous over that interval, there exists a maximum and minimum over that interval
23
Q

A
0
24
Q
(sin x)1 =
A
cos x
25
(sec x)1 =
sec x tan x
26


27
If the second derivative of f is negative, what does that say about the derivative
The derivative is decreasing over that interval
28
If the derivative is positive, what does that tell you about the function?
That it is increasing
29
(tan x)1 =
sec2x
30


31
(ex)1
ex


