Tan, cos, sin

Question 1

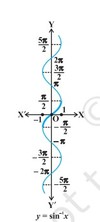
Graph of sin^-1x?

Answer 1

sine : R → [– 1, 1]

sin^-1 : [–1, 1] → [−π/2, π/2]

Question 2

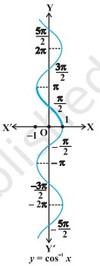
Graph of cos^-1x?

Answer 2

cos : R → [– 1, 1]

cos–1 : [–1, 1] → [0, π]

Question 3

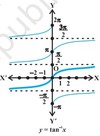
Graph of tan^-1x?

Answer 3

tan : R – { x : x = (2n + 1) π/2 , n ∈ Z} →R

tan–1 : R → [−π/2, π /2]

Question 4

Graph of csc^-1x?

Answer 4

cosec : R – { x : x = nπ, n ∈ Z} →R – (– 1, 1)

cosec–1 : R – (–1, 1) → [-π/2,π/2]-{0}

Question 5

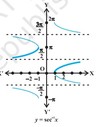
Graph of sec^-1x?

Answer 5

sec : R – { x : x = (2n + 1) π/2 , n ∈ Z} →R – (– 1, 1)

sec^-1 : R – (–1,1) → [0, π] – { π/2 }

Question 6

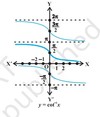
Graph of cot^-1x?

Answer 6

cot : R – { x : x = nπ, n ∈ Z} →R

cot–1 : R → (0, π)

Question 7

Summarize

Answer 7

Question 8

Basics

Answer 8

sin (sin^-1 x) = x, x ∈ [– 1, 1]

sin^-1 (sin x) = x, x ∈ [- π/2, π/2]

Question 9

Properties

1)

(i) sin^-1 (1/x )=
(ii) cos^-1 (1/x )=
(iii) tan^-1 (1/x )=

Answer 9

cosec^-1x, x ≥ 1 or x ≤ – 1

sec^-1x, x ≥ 1 or x ≤ – 1

cot^-1 x, x >0

Question 10

2)

(i) sin^-1 (–x) =
(ii) tan^-1 (–x) =
(iii) cosec^-1 (–x) =

Answer 10

– sin^-1 x, x ∈ [– 1, 1]

– tan^-1 x, x ∈ R

– cosec^-1x, | x | ≥ 1

Question 11

3)

(i) cos^-1(–x) =
(ii) sec^-1(–x) =
(iii) cot^-1 (–x) =

Answer 11

= π – cos^-1 x, x ∈ [– 1, 1]

π – sec^-1 x, | x | ≥ 1

π – cot^-1x, x ∈ R

Question 12

4)

(i) sin^-1 x + cos^-1 x =
(ii) tan^-1 x + cot^-1 x =
(iii) cosec^-1 x + sec^-1 x =

Answer 12

π/2 , x ∈ [– 1, 1]

π/2 , x ∈ R

π/2 , | x | ≥ 1

Question 13

5)

(i) tan^-1x + tan^-1 y =
(ii) tan^-1x – tan^-1 y =
(iii) tan^-1x + tan^-1 y =

Answer 13

tan^-1 (x + y )/(1– xy) , xy < 1

tan^-1 ( x – y)/(1 + xy) , xy > – 1

π + tan^-1 (x + y )/(1– xy), xy > 1; x, y > 0