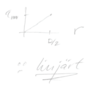Teorifrågor - Gamla tentor Flashcards
(33 cards)
En metod för att uppskatta töjningen 𝜀 i en stång är att dividera förlängningen 𝛿 med dess ursprungslängd L. Vad måste vara uppfyllt för att detta ska vara en pålitlig metod? 𝜀 = 𝛿/L
𝛿 << L
Hos en balk kan man beräkna förskjutningen w(x) vinkelrätt mot balken med bra hjälp av den Elastiska linjens ekvation. Vad krävs för att detta ska vara en bra metod?
Att vinkelförändringarna (rotationerna) i varje punkt längs balken är små (några få grader).
En massiv axel med diametern D, tillverkad av ett linjärt elastiskt ideal-plastiskt material med sträckgränsen 𝜎s, är utsatt för ett vridande moment M. Hur stort moment kan maximalt tillåtas och om säkerhetsfaktorn mot kollaps ska vara lika med 2?
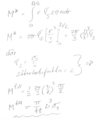
Hur definieras begreppet huvudspänning?
En normalspänning på en skjuvspänningsfri yta.
Antag att vi approximerar en verklig komponent med begreppet stång. Vilken typ av utbredda laster kan isåfall tas hänsyn till?
Enbart laster som verkar i stångens egen riktning. T.ex. egentyngden om stången hänger vertikalt!
Längs en balk varierar tvärkraften linjärt. Hur varierar då det böjande momentet?

En stel detalj bär en vertikal kraft P enlikt figuren nedan. Den stela detaljen hålls på plats av två fjädrar med fjäderkonstanten k. Beräkna den kritiska kraftnivån då anordningen blir instabil.


Vad menas med ett hydrostatiskt belastningstillstånd?
Att belastningen är lika stor i alla riktningar. 𝜎1=𝜎2=𝜎3=𝜎0 där 𝜎0 är den hydrostatiska belastningen.
En lång slank rak verklig detalj med längden L och den konstanta tvärsnittsarean A belasttas av en kraft N i detaljens längdriktning. Använd modellbegreppet “stång” och härled en formel för hur förlängningen 𝛿 kan beräknas på grund av kraften N. Antag vidare att ett linjärt elastiskt beteende enligt Hookes lag är rimligt där elasticitetsmodulen E kan antas vara given.
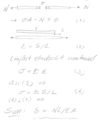
Längs en balk varierar en utbredd last/längdenhet q(x) linjärt. Ange ett generellt matematiskt uttryck för hur förskjutningen i z-led w(x) varierar oavsett randvillkor!

En ihålig axel med ytterdiametern 2D och innerdiameter D är utsatt för ett vridande moment M. Materialet i axeln är linjärt elastiskt ideal-plastiskt med sträckgränsen 𝜎s. Hur många procent större moment kan axeln bära innan kollaps inträffar om den istället görs massiv med samma ytterdiameter som tidigare?

Vilken fråga försöker man svara på med hjälp av en flythypotes?
När plastisk flytning inträffar.
Ett sätt att approximera ett verkligt fackverk är att betrakta detsamma som ett “stångbärverk”. Nämn två utmärkande drag hos en beräkningsmodell som kan kallas för ett stångbärverk?
- Alla knutpunkter betraktas som momentfria leder
- Varje del (stång) kan bara bära en drag- eller tryckkraft
Vid vårt stadium av balkteori begränsade vi oss från allmän 3D-balkböjning, s.k. “plan böjning” där laster och förskjutningar finns i ett och samma plan. För att denna förenkling skall vara tillämpbar krävs också en begränsning med avseende på balkens geometri. Beskriv denna begränsning.
Balkens tvärsnitt måste ha minst en symmeri som sammanfaller med belastningsplanet.
En massiv axel med diametern D utsätts för ett vridande moment. Beräkna det maximala moment som axeln kan bära innan genomplasticering och kollaps inträffar om materialets skjuvsträcksgräns är 𝜏s. Materialet kan antas vara linjärt elastiskt-idealplastiskt.

Hur många obekanta storheter har ett 3D linjärt elasticitetsproblem?
6 spänningskomponenter, 6 töjningar, 3 förskjutningskomponenter ⟹ 15 obekanta storheter och 15 ekvationer
Vid en linjär fjäder pratar man om en fjäderkonstant ofta kallad k. Vid analys av vårt stångbegrepp kan motsvarande konstant identifieras. Hur ser den ut om längden L, tvärsnittsarean A och elasticitetsmodulen E är givna?

En rektangulär balk har i ett visst snitt tvärkraften T. Rita en bild på hur skjuvspänningen i detta snitt varierar m.a.p. z.
För att vid ett fleraxligt spänningstillstånd kunna avgöra om plasticering inträffar har vi i vår kurs diskuterat två olika s.k. flythypoteser. Ange namnen på dessa båda!
Tresca och von Mises flythypoteser.
I den matematiska modell vi kallar stång har vi använt ett linjärt töjningsmått där längdändringen antas vara mycket mindre än ursprungslängden. Visa hur detta töjningsmått ser ut lokalt i tex. En stång med svagt varierande tvärsnittsarea. (Vår makroskopiska töjningsdefinition duger inte längre.

Med hjälp av vår diskuterade balkmodell så kan vi räkna ut hur en förskjutning w(x) vinkelrätt mot balken pga tex en utbredd belastning q(x). Hur påverkas denna förskjutning om balken också påverkas av en axiell belastning N?
Inte alls! I vår modell har vi approximerat så att den effekten inte innehålls!
En cirkulär axel är tillverkad av ett linjärt elastiskt ideal-plastiskt material med skjuvgränsen 𝜏s. Hur stor maximalt vridanden moment kan man då belasta axeln med innan den helt kollapsar om axeln har diametern D?
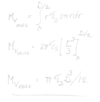
En enaxligt belastad provstav belastas till det att den når sin sträckgräns 𝜎s. Hur stor är då den största sjuvspänningen man kan hitta i provstaven?

En slank verklig detalj har längden L, tvärsnittsarean A, längdutvidgningskoefficienten 𝛼 och elasticitetsmodulen E. Ingen av ändarna kan förflytta sig. Antag att en stångapproximation är lämplig och beräkna hur stor spänning som uppkommer i stången om temperaturen höjs med 𝛥T=T-T0. Antag vidare att stången är spänningsfri då T-=T0.