What Is Bloom’s 2 Sigma Problem? (& Why It Matters In Education)

In high school, I sucked at organic chemistry. Stuffed into a small classroom with 40 other students, I was often distracted by other kids, felt too shy to ask questions, and could easily fly under the radar if I didn’t understand something. So I did.

But my mother wouldn’t have one bar of it. She’d be darned if her otherwise straight-A daughter was going to bomb science. So she hired a tutor for me.

Now it was just me, my tutor, and all the knowledge gaps I had been sweeping under the carpet until then. The tutor quickly assessed my unique strengths and weaknesses and provided instruction that was tailored to bring me up to speed really quickly.

By the end of the semester, I was crushing organic chemistry. And by “crushing”, I mean I scored higher than my nerdy friend whose report card looked more like a battery catalogue.

Bless my mother in all her wisdom.

The astonishing difference between my D grade (pre-tutoring) and A grade (post-tutoring) actually has a name… and it’s Bloom’s 2 Sigma Problem.

It was coined when educational psychologist Benjamin S. Bloom noticed that tutored students routinely perform two standard deviations (“2 σ”) above the average of the conventional class. And the question asked by educators everywhere is: how can we replicate the learning gains of one-on-one tutoring in more scalable teaching settings?

In this article, you and I are going to explore Bloom’s 2 Sigma problem in much greater detail, answering just about every question ever asked about it by frustrated educators, students, and parents.

Importantly, we’ll also address how to overcome the discrepancy in the quality of education between conventionally-taught classes and privately-tutored individuals because few people can afford the latter… and why should they suffer?

So, if you’d like your education (whether you are giving or receiving it) to reflect the gains of private tutoring without the price tag, come along for the ride…

Where Did Bloom’s 2 Sigma Problem Come From?

Bloom’s investigation began in the early 1980s at the University of Chicago, where his doctoral students (Anania and Burke) compared three instructional conditions:

Conventional classroom learning (~30 students per teacher),
Mastery-learning classroom (same class size but with formative testing and corrective feedback), and
One-on-one or very small-group tutoring (one tutor for each student or three students).

The results were striking:

The mastery learning group outperformed the conventional class by roughly one standard deviation (1 σ).
The one-on-one tutoring group outperformed by roughly two standard deviations (2 σ).
The need for corrective work under tutoring was very small; a sign the path to mastery was efficient.

Bloom’s conclusion: while one-on-one tutoring is extremely effective, it is too costly and difficult to provide at scale. Hence, the “problem” is: how do we deliver something like that in a classroom, online, or through scalable systems?

How Does Bloom’s 2 Sigma Problem Work, Cognitively?

At heart, what tutoring or mastery learning gives a student is personalized attention, the kind that adapts in real time to what you actually understand (and what you don’t).

Think of it like having a GPS for your brain. When you veer off course, it doesn’t keep shouting the same directions at you; it reroutes you instantly. That’s what a good tutor does! They slow down when you’re struggling, speed up when you’re cruising, and help you tackle concepts that are just beyond what you can currently do on your own.

Psychologists call this the Zone of Proximal Development (ZPD), the sweet spot where learning feels challenging but still doable. Classroom instruction can’t always hit that target for every student at once, but tutoring and adaptive learning tools can. They meet you right where you are and nudge you just far enough forward to make real progress!

Moreover:

When a learner works one-on-one, the tutor can detect misconceptions early and correct them immediately, reducing wasted time and memory of errors.
The tutor can match instruction to the student’s pace, meaning the working memory load is managed optimally and the student isn’t left grappling with too much or waiting too little.
Frequent formative assessments and corrective work help to strengthen neural pathways via retrieval, feedback, and elaboration more effectively.

Spelled out like this, it’s not hard to see why these processes (reduced error, optimal pacing, and targeted repetition) offer cognitive advantages over “once-size-fits-all” classroom instruction!

In short: the one-on-one condition optimizes the variables that matter for learning: individual attention, immediate corrective feedback, and pacing.

What Are the Key Principles of the 2 Sigma Problem?

Here are the major levers Bloom identified (and which subsequent researchers continue to explore) that contribute to the dramatic performance improvement of one-on-one instruction:

Mastery Learning: Students must achieve a high level of understanding (e.g., 90 %) in prerequisite material before moving on. This prevents cumulative deficits.
Tutoring or Individualized Instruction: The highest-performing group had individualized attention and pace matched to the learner.
Frequent Formative Assessments and Corrective Procedures: These feedback loops keep the learner aligned and prevent wasted effort.
Optimal Pacing and Content Matching: Instruction changes when the student is ready, preventing unnecessary waiting or hurrying, thereby reducing cognitive load, and maximizing learning time.
Scalable Methods Seeking to Replicate Tutoring Gains: As Bloom phrased it, “The problem is not tutoring; the problem is doing as well as tutoring in group settings.”

Great! So why should you give a f— ?

Why Does the 2 Sigma Problem Matter for Learning, Teaching, and Memory?

Because it holds up a mirror to what is possible! And what we fall short of in typical instruction, which should matter a whole lot to you if you’re an educator or student in any group setting.

Here’s why it’s meaningful:

Unlocking Potential: Bloom’s data suggest that the barrier for the average student isn’t necessarily ability, it’s instructional design. Effective tutoring elevated many average students to the level of the top students in conventional classes. (This is exactly what happened to me in organic chemistry!)
Instructional Design Imperative: If one-on-one tutoring yields 2 σ gains, educators and instructional designers must ask: which elements of that condition can we embed into broader instruction?
Memory Implications: Because tutoring and mastery learning include frequent feedback and corrective work, they reduce the encoding of errors, strengthen retrieval pathways, and manage cognitive load: fundamental elements of durable learning.
Equity and Access: The 2 Sigma gap highlights the disadvantage faced by students without access to individualized instruction; and the challenge of scaling high-quality learning for all. If my mom had never hired that tutor, I would have gotten crappy science scores, which would have hurt my application to university. I was privileged to receive this individual instruction. Most people are not.

In short, the 2 Sigma Problem may be framed as a research curiosity, but it has practical significance for anyone designing study systems (you!) or teaching others (educators!).

The real question, then, is this: how can we bring the benefits of one-on-one tutoring to everyone, without needing an army of tutors?

That’s where smart learning tools come in.

Modern study methods like adaptive digital flashcards can’t replace a human teacher, but they can mimic some of tutoring’s most powerful ingredients: constant feedback, personalized pacing, and adaptive review. Here’s how…

How Do Digital Flashcards Leverage the 2 Sigma Problem?

Flashcards alone aren’t tutoring, but when used smartly, they replicate several of the core tutoring features that contribute to the 2 σ effect:

Frequent low-stakes assessment: Every flashcard compels you to retrieve information from memory, akin to the formative questions that a human tutor might ask you along the way.
Immediate feedback: You then “flip” the card, see whether you were correct, and rate yourself according to how well you knew the answer. In flashcard apps like Brainscape, that rating scale would be 1 to 5 with 1 being “I didn’t know this at all” and 5 being “I knew this perfectly.”

Brainscape flashcard mobile study experience

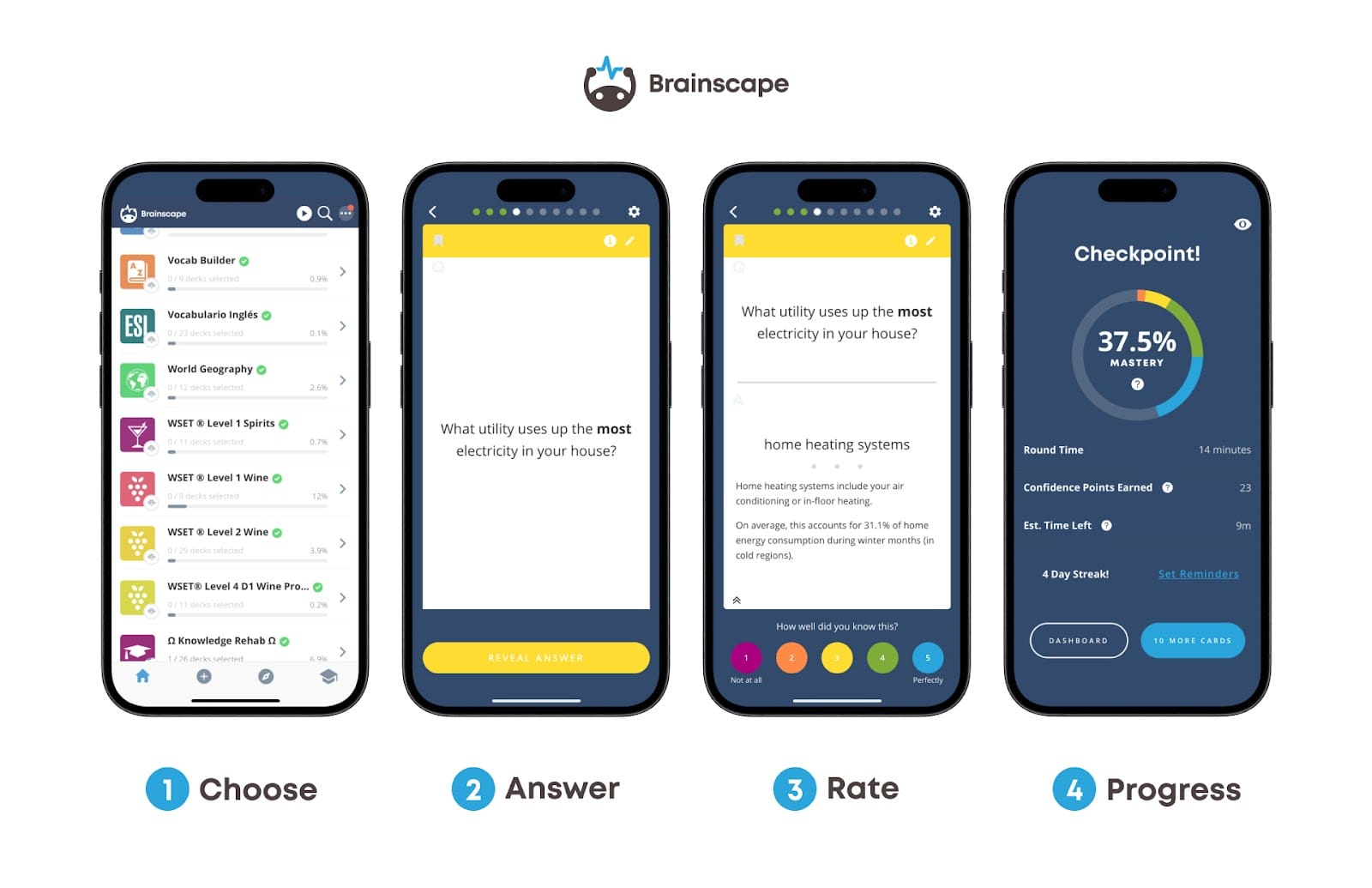
Adaptive pacing: If you struggle with a flashcard (rate it a 1 or 2), the algorithm will show it to you more often; if you know it well (rate it a 4 or 5), you’ll see it less, which mirrors the individualized pacing that a savvy tutor would impose on their students to keep them in the ZOPD.
Focused corrective work: The flashcards you get wrong become opportunities for targeted corrective review, just like a tutor would intervene!

While a digital flashcard system doesn’t replace full tutoring, it captures key levers of what makes tutoring so effective and scales them for solo learners. Platforms like Brainscape and Anki (and many others) embed the same principles Bloom identified: mastery, feedback, pacing, and retrieval.

So, What’s the Takeaway?

Bloom’s 2 Sigma Problem reminds us that the conditions under which you learn matter as much as what you learn. Organic chemistry is hard! Learning it in a classroom full of hormonal teenagers, while beset with a crippling lack of confidence, is even harder.

Teaching fewer students at a time, giving frequent feedback, and pacing to mastery can radically accelerate learning. But since this is not always possible, you—the learner—may have to take matters into your own own hands, which means:

Seek frequent assessment and feedback, even if that means self-quizzing.
Use tools that adapt to your pace and give extra practice where you’re weak (like flashcards).
Embrace methods designed around mastery, not just moving through the curriculum.

And yes, while you may not have a personal tutor beside you 24/7, you can harness tutoring features via smart study strategies and digital tools. One-on-one remains gold-standard, but the science of the 2 σ gap gives you a blueprint for how to study more effectively anyway.

Additional Reading (if you’re a sucker for punishment)

If you loved this, you’ll also love these other nerdy science articles we wrote about:

References

Bloom, B. S. (1984). The 2 Sigma Problem: The Search for Methods of Group Instruction as Effective as One‐on‐One Tutoring. Educational Researcher, 13(6), 4-16. https://doi.org/10.3102/0013189X013006004

Cañigueral, R., Ward, J., & Hamilton, A. F. de C. (2021). Being watched increases task performance through enhanced motivation. Scientific Reports, 11(1). https://doi.org/10.1038/s41598-021-99583-2

de Bruin, A. B. H., & van Merriënboer, J. J. G. (2023). Worth the effort: Start and stick to desirable difficulties to improve learning. Educational Psychology Review, 35. https://doi.org/10.1007/s10648-023-09766-w

Hanushek, E. A. (2020, Fall). Two sigma tutoring: Separating science fiction from science fact. Education Next, 20(4). https://www.educationnext.org/two-sigma-tutoring-separating-science-fiction-from-science-fact/

Tan, S. L., & Tan, A. C. (2021). Peer learning and social motivation in higher education: A meta-analysis. Journal of Educational Psychology, 113(2), 228-244. https://doi.org/10.1037/edu0000473