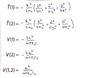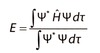4b: Quantum Mechanics

Question 1

What is the schrodinger equation for a particle in one and three dimensions?

Answer 1

Question 2

Define the normalisation constant and give its mathematical definition.

Answer 2

The normalisation constant makes sure the vaule of ψ² is constant over all values.

Question 3

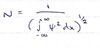
What are the three requirements for ψ?

Answer 3

Single valued at all points

Never infinite

Continuous and smooth (and its derivitive)

Integration over all values must be finite

Question 4

What is Heisenbergs uncertainly principle?

Answer 4

It is impossible to specify simaltaneously, with arbitrary precision, both the momentum and position of a particle.

ΔpΔx >= ½ħ

Question 5

What are the limits of the particle in a box?

Answer 5

The potential energy, Vψ, within the box is 0, and is infinite outside the box walls.

Question 6

What does the energy of a particle in a box depend on?

Answer 6

The mass of the particle and the length of the box.

Question 7

When can particles in a box tunnel?

Answer 7

When the walls are a finite barrier and the potential of the walls aren’t infinite, there is always a chance of tunneling.

Question 8

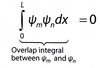
How do you define orthogonal wavefunctions?

Answer 8

Question 9

How does the number of energy levels change when the particle in a box is expanded to three dimensions?

Answer 9

There is an energy level for each dimension, hence when the energy levels are n= 1, 2, 3; 6 different energy levels with the same energy are possible.

Question 10

How is the particle in a ring equation different to the normal equation?

Answer 10

The particle in a ring uses moment of inertia because instead of a distance in x, and angle is used to define its position. The boundary condition is therefore that adding 2π doesn’t change the wavefunctions value.

Question 11

How is a complex wavefunction accounted for?

Answer 11

ψ² is calculated by ψψ*, each energy level has 2 degenerate energy levels with a positive and negative value of m_l.

Question 12

How is the schrodinger equation different for a harmonic oscillator?

Answer 12

The potential energy is defined by the potential energy of a spring and the force constant, V = ½kx²

The vibrational energy here can never be zero. Reduced mass is used in the case of a diatomic to simplify the equation to a single particle oscillating about a centre of mass.

Question 13

What is the energy operator called and what is the general operator for other variables.

Answer 13

The energy operator is the hamiltonian operator.

All observables are defined by their own operator, generally called a hermitian operator and they must all give real eigenvalues.

Question 14

How do you convert from classical variables to quantum?

Answer 14

All observable variables become operators.

Question 15

How do you adjust the schrodinger equation for time dependance?

Answer 15

As time is another dimension, the wavefunction has to include that variable. This means that energy is no longer directly included in the equation.

Question 16

What is the equation for the hydrogenic atom and what assumptions have been made?

Answer 16

Assume nucleus is fixed due to large mass ratio difference. The potential energy is defined by Coulombs potential energy.

To account for the nucleus moving, replace the mass of the electron with a reduced mass.

Question 17

How can the schrodinger equation for the hydrogenic atom be made easier to solve?

Answer 17

By switching from Cartesian (x,y,z) coordinates to spherical polar coordinates (r = radial distance, θ = zenith, φ = azimuth)

This is known as the seperation of variables.

ψ(r,θ,φ) = R(r) Y(θ,φ) = R(r) Θ(θ) Φ(φ)

Where R(r) is the radial wavefunction and Y(θ,φ) is the spherical harmonics/angular components.

Question 18

Define which quantum numbers the seperated variables of the hydrogenic atom depend on.

Answer 18

R(r) depends on

• Principle quantum number, n = 1, 2, 3…
• Orbital angular momentum quantum number, l = 0, 1, 2, …, n - 1

Θ(θ) depends on

• Orbital angular momentum quantum number, l = 0, 1, 2, …, n - 1
• Magnetic quatum number (magnitude), m_l = l, l - 1, l - 2, …, -l

Φ(φ) depends on

• Magnetic quatum number, ml = l, l - 1, l - 2, …, -l

Question 19

What is the definition of an atomic orbital, a shell and a subshell?

Answer 19

An atomic orbital is a one-electron wavefuntion for an atom.

A shell is all AOs that have the same value of n.

A subshell are AOs with the same value of n but different values of l.

Question 20

What is the radial distribution function?

Answer 20

r²R(r)²dr which gives the probablility of finding an electron in a shell of thickness dr. The probability across all values of r is normalised to 1.

Question 21

What values of m_L corrospond to p_z, p_y and p_x?

Answer 21

m_L = 0 corrosponds to p_z.

m_L = ±1 has components in both p_y and p_x. Φ is complex for both p_y and p_x.

Question 22

How can real d orbitals be obtained from the different complex values of p_-1,-2,1,2?

How can the angular components of both d and p orbitals be simplified?

Answer 22

d₀ is real and corrosponds to d_z².

By combining complex orbitals, real orbitals can be found.

By writing them in cartesian coordinates.

Question 23

How is electron spin defined? How is this applied to a spacial orbital?

Answer 23

The spin quantum number, s = ½

The spin magnetic quantum number, m_s = ±½ where the α electron = ½ and the β electron = -½.

The spacial orbital is split from ψ(x,y,z) to ψ(x,y,z)α(ω) and ψ(x,y,z)β(ω).

Question 24

In simple terms, note all the interactions for a single particle and for two particles, then define each term for the equation with two particles.

Answer 24

Single particle: E = T(1) + V(1)

Two particles: E = T(1) + T(2) + V(1) + V(2) + V(1,2)

Question 25

Define the schrodinger equation for a many electron system.

Answer 25

H(1,2,...,N)Ψ(1,2,...,N) = EΨ(1,2,...N) The operator and wavefunction represent a many electron system.

Question 26

Write out and shorten a 1s orbital using wavefunctions.

Answer 26

Ψ(1,2) = 1s(1)α(1) 1s(2)β(2) = 1sα 1sβ = 1s²

Question 27

What is the meaning and what are the implications of the Pauli exclusion principle on writing wavefunctions for many electron atoms?

Answer 27

The Pauli exclusion principle states that: No more than 2 electrons can occupy the same spacial orbital and if they do, they must have opposite spins. This means for many electron wavefunctions, when the electrons change position, the sign must change. This is called being **antisymmetric**. This has to be done by Ψ_A = ψ(1,2) - ψ(2,1) = ψ₁(1)α(1)ψ₁(2)β(2) - ψ₁(2)α(2)ψ₁(1)β(1). This can also be turned into a 2x2 matrix called the slater determinant with corrosponding wavefunctions in opposite corners.

Question 28

How can you estimate the energy of a wavefunction if you only have an approximate value? How does the variation principle apply to this and how can it be accounted for?

Answer 28

Where dt is the product of all the variables in the wavefunction across all values. The variation principle says that the energy of the approximate wavefunction is always higher than the exact solution, E \> E₀. As approximate wavefunctions contain its own adjustable parameters, they should be tested to find the lowest solution as it will be the most accurate.

Question 29

How does penetration and shielding change when moving from a hydrogenic atom to a multi-electron atom?

Answer 29

In the hydrogenic atom, the s and p orbitals are degenerate as energy only depends on the principle quantum number. However s orbitals penetrate closer to the nucleus and experience less shielding than the p orbitals in multi-electron systems.

Question 30

What is the Born-Oppenheimer approximation?

Answer 30

The electrons in an atom are assumed to move round a stationary nucleus and the nuclei slowly move according to the averaged movement of electrons. The schrodinger equation can then be seperated into 2 equations.

Question 31

Define a potential energy curve and a potential energy surface.

Answer 31

A potential energy curve shows how molecular energy depends on internuclear seperation. A surface applies when more than 2 atoms are involved.

Question 32

Give the terms of the schrodinger equation for H₂.

Answer 32

Question 33

How can MO wavefuctions be found from AOs? How does this translate to bonding and antibonding orbitals? How can they be simplified?

Answer 33

MOs can be approximated by LCAO, or liner combination of atomic orbitals. Bonding: ψ₁ = c_Aψ_A + c_Bψ_B where ψ_A = ψ_A1s and ψ_B = ψ_B1s Antibonding: ψ₂ = c_Aψ_A - c_Bψ_B When these functions are squared they have either ±c_Ac_Bψ_Aψ_B which accounts for the difference in probabilities. When the nuclei are identical, c_A = c_B and can be replaced with N₁ for bonding and N₂ for antibonding (as the normalisation for bonding and antibonding are not equal)

Question 34

When are orbitals labelled σ, and when are they labelled with g/u?

Answer 34

They are a σ orbital if the phase doesn't change when reflected in any plane passing through both nuclei. If there is a centre of inversion, if the phases change when they are inverted they have the label u, if not they have the label g.

Question 35

Why doesn't He₂ ever form?

Answer 35

Because its bonding orbitals are less bonding than its antibonding orbitals are antibonding.

Question 36

Describe the general expression for the MO by LCAO for multiple atoms. What should you look out for when describing bonding MOs?

Answer 36

It combines every wavefunction with its normalisation for all atoms. These normalisation values can be calculated for each MO. For the 2nd row diatomics this would include the 1s, 2s, 2px, 2py and 2pz orbitals however the 1s orbitals can often be ignored as they will barely overlap. Also the σ and π orbitals can often be seperated into different functions. Make sure the signs are correct, bonding doesn't mean AOs have to be the same phase!