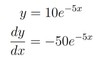Week 10 Flashcards
Find the derivative of the following functions by first principals (i.e. using the definition of the derivative).
y= 2x−5

Find the derivative of the following functions by first principals (i.e. using thedefinition of the derivative).
y= 5x2

Find the derivative of the following functions by first principals (i.e. using thedefinition of the derivative)
y= 4x−3x2

Find the derivative of the following functions by first principals (i.e. using thedefinition of the derivative).
y=x2−2x+√7

Find dydx for each of the following functions
y= 4x−7
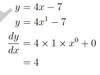
Find dydx for each of the following functions.
y=−7x+ 2
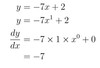
dydx
y= 3x2−4x+ 8

dydx
y= 5x3−8x2+ 9x+ 1
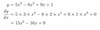
dydx
y=−6x4+ 10x3
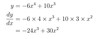
dydx
y= 6 sin(x) +x2
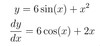
dydx
y= 9 cos(x)−3 sin(x)
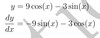
dydx
y=−4 cos(x) + 7 sin(x)
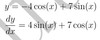
dydx
y=e3x+ 4
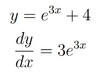
dydx
y= 6e2x+x2

dydx
y= 10e−5x