Tree Strategies Flashcards
Check if Two Binary Trees are Identical
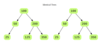
Given the roots of two binary trees, determine if these trees are identical or not. Identical trees have the same layout and data at each node. Consider the following two identical binary trees that have the same layout and data.
It is not necessary that trees that have the same data are identical trees. Trees that have the exact same data may not be structurally identical. For example if you look at the two trees below, although they have the same data, they are not identical.
Runtime Complexity: Linear, O(n).
Memory Complexity: O(h)
The recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary tree h. It will be O(log n) for a balanced tree and in the worst case can be O(n).
This problem can be effectively solved using a recursive solution. The base case of recursion for this solution is if both nodes being compared are null, or one of them is null.
Two trees ‘A’ and ‘B’ are identical if:
- data on their roots is the same or both roots are null
- left sub-tree of ‘A’ is identical to the left sub-tree of ‘B’
- right sub-tree of ‘A’ is identical to the right sub-tree of ‘B’
To solve this problem, we’ll do a depth-first traversal on both trees simultaneously and keep comparing the data at each level.
Write an In-Order Iterator for a Binary Tree
We are given the root node of a binary tree. We have to write an iterator that takes in this root and iterates through the nodes of a binary tree in an inorder way. The expectation is to write two critical methods of any iterator: hasNext() and getNext(). Consider the following binary tree. Repeatedly calling hasNext() and getNext() functions on the above binary tree should return nodes in the following sequence: 25, 50, 75, 100, 125, 200, 300.
Runtime Complexity: Linear, O(n).
Memory Complexity: O(h).
An iterative solution has O(h) memory complexity as it instantiates a stack that has to store information up to the height of the binary tree (h). It will be O(logn) for a balanced tree and in the worst case, can be O(n).
We strongly recommend that you read the solution for iterative inorder traversal. It will help you better understand this solution. In this problem, we will need a stack to help us navigate the binary tree inorder and maintain the necessary state. Let’s see some basic rules for writing this iterator:
- Stack will contain the next element at top, to return on getNext().
- hasNext() will only check whether the stack is empty or not.
To be able to carry out the aforementioned steps, we will need to set up a stack in the correct state at iterator construction. For that purpose, we push all elements from the root up to the leftmost node of the binary tree at iterator construction.
The next task is to implement the getNext() method. It requires returning the next element in inorder traversal. It can be done by just returning the top node from the stack AND also setting up the stack in the correct state for the next getNext() call. For the latter, we look at the right child of the top node of the stack and if it’s non-null, we push all the nodes from this node to its leftmost node on to the stack.
Iterative Inorder Traversal
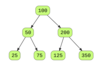
Given a binary tree, write an iterative algorithm to traverse the tree inorder. Let’s look at the tree below as an example.
Inorder traversal of the above tree should visit the nodes in the following order: 25, 50, 75, 100, 125, 200, 350.
Runtime Complexity: Linear, O(n).
Memory Complexity: O(h).
The iterative solution has O(h) memory complexity as it instantiates a stack that has to store information up to the height of binary tree h. It will be O(log n) for a balanced tree and can be O(n) in the worst case.
The inorder traversal of a binary tree starts from the root. First, it visits the left node (L), followed by the current node (N), and finally, the right node (R). This is repeated for every node during the traversal. An easy way to remember this is LNR, the node comes in the middle. For a BST, inorder traversal will always print nodes in an ascending order (based on their values).
For an iterative inorder traversal, a stack is used to track the nodes. Here is the pseudocode.
initialize the current_node as root.
create an empty stack stk.
Push the current_node in stk and set current_node = current_node->left until current_node becomes NULL.
if stk is not empty and current_node == NULL then
Print the top element from stk
Pop the top element from stk and set current_node = element_popped->right
go to step 3
if current_node is null and stack is empty then algorithm terminates.
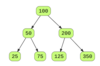
Inorder Successor BST
The inorder successor of a node in a binary Search Tree (BST) is the next node in inorder traversal. Write a method to find the inorder successor of a given value “d” in a BST.
Consider the following BST.
In the above tree
- Inorder successor of 25 is 50
- Inorder successor of 50 is 75
- Inorder successor of 75 is 100
- Inorder successor of 100 is 125
- Inorder successor of 125 is 200
- Inorder successor of 200 is 350
- Inorder successor of 350 is NULL since it is the last node
Runtime Complexity: Logarithmic, O(logn).
Memory Complexity: Constant, O(1).
A naive solution of this problem would be doing an in-order traversal of the BST. Once d is found, it returns the next node in the traversal. The runtime of this approach is linear. We can do better than linear in this problem if we closely look at the possible locations of the in-order successor. Let’s define some rules around that:
Find the value d in BST. If d has a right child then the left most child in right child’s subtree will be the in-order successor of d. This would also be the child with the minimum value in that subtree.
Find the value d in BST. If d has no right child then:
in-order successor is NULL if d is right most node in the BST i.e. last node in the in-order traversal
in-order successor is the node with minimum value higher than d in the parent chain of d
Level Order Traversal of Binary Tree
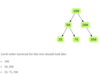
Given the root of a binary tree, display the node values at each level. Node values for all levels should be displayed on separate lines. Let’s take a look at the below binary tree.
Runtime Complexity: Linear, O(n).
Memory Complexity: Linear, O(n).
Iterative solution has O(n) memory complexity as it instantiates queues that can take space upto n/2 nodes.
All we need is an end-of-level marker. It can be an empty queue or a NULL pointer. NULL acts as the end-of-level marker in the current_queue. Here is how the current_queue initially looks like with the NULL marker at level ‘0’.
We will dequeue the nodes from the current_queue, print the node’s data, and enqueue the node’s children to the current_queue. If we see a NULL node at the queue’s head, we have processed all nodes for the current level. In order to indicate a new level, we will print a line break (‘\n’) and add a NULL node (level marker) to the current_queue. When the current_queue is empty, we will terminate the loop since all nodes in the tree have been processed.
Is Binary Search Tree?

Given a Binary Tree, figure out whether it’s a Binary Search Tree. In a binary search tree, each node’s key value is smaller than the key value of all nodes in the right subtree, and are greater than the key values of all nodes in the left subtree i.e. L < N < R.
Runtime Complexity: Linear, O(n).
Memory Complexity: O(h).
Recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary tree h. It will be O(log n) for a balanced tree and in the worst case can be O(n).
One nice property of a Binary Search Tree is that its inorder traversals are always sorted. We can use this property to check whether or not a given binary tree is a BST. Just do a regular inorder traversal and keep track of the last seen node (prev), then check whether the current node’s value is greater than or equal to the previous (prev) node’s value.
Convert Binary Tree to Doubly Linked List
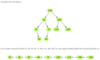
Convert a binary tree to a doubly linked list so that the order of the doubly linked list is the same as an in-order traversal of the binary tree. After conversion, the left pointer of the node should be pointing to the previous node in the doubly linked list, and the right pointer should be pointing to the next node in the doubly linked list.
Runtime Complexity: Linear, O(n). Runtime complexity is based on the number of nodes in the tree.
Memory Complexity: Linear, O(h).
Recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary tree ‘h’. It will be O(log n) for balanced tree and in worst case can be O(n).
In an in-order traversal, first the left sub-tree is traversed, then the root is visited, and finally the right sub-tree is traversed.
One simple way of solving this problem is to start with an empty doubly linked list. While doing the in-order traversal of the binary tree, keep inserting each element output into the doubly linked list. But, if we look at the question carefully, the interviewer wants us to convert the binary tree to a doubly linked list in-place i.e. we should not create new nodes for the doubly linked list.
This problem can be solved recursively using a divide and conquer approach. Below is the algorithm specified in simple words.
Start with the root node and solve left and right sub-trees recursively
At each step, once left and right sub-trees have been processed:
- fuse output of left subtree with root to make the intermediate result
- fuse intermediate result (built in the previous step) with output from the right sub-tree
to make the final result of the current recursive call
Print Tree Perimeter

Given the root node of a binary tree, print the nodes that form the boundary (perimeter).
In the following tree, the highlighted nodes form the perimeter. The expected output for the below tree would be 1, 2, 4, 9, 8, 10, 7, 3.
Runtime Complexity: Linear, O(n).
Memory Complexity: O(h).
Recursive solution has O(h) memory complexity as it will consume memory on the stack up to height of the binary tree h. It will be O(logn) for a balanced tree and in the worst case can be O(n).
We will print the perimeter of the binary tree in three passes. Here is how the algorithm looks:
Print the root node. Print the left boundary in top-down order. Print the leaf nodes in left-right order. Print the right boundary in bottom-up order. We will push the node values in a stack here. Once we hit the leaf node, we will pop all elements of the stack while printing them.

Connect Same Level Siblings

Given a binary tree, connect its siblings at each level.
Runtime Complexity: Linear, O(n).
Memory Complexity: Constant O(1).
A binary tree is a data structure made up of nodes, where each node contains data and up to two children: the “left” reference and the “right” reference. Nodes with the same parent node are called siblings. We need to connect all siblings at each level.
In a level order traversal of a tree, all nodes are processed by depth; first the root, then the children of the root and so on. It is equivalent to a breadth-first-search from the root.
Each node in the above binary tree has one more pointer i.e. next (aka sibling) along with the left and right pointers. ‘next’ is used to connect one node to the other.
Here’s how the algorithm works:
Given the starting node at level ‘x’ (where nodes at level ‘x’ are connected):
Traverse the nodes at level ‘x’ from left to right while connecting the siblings at level ‘x+1’.
Now that siblings at level ‘x+1’ are connected, use the head node (left-most) of level ‘x+1’ and
apply the same approach on ‘x+2’.
Keep running these steps till we run out of levels.
To connect the nodes at a level, given the head of that level, we’ll use a prev pointer along with current to keep track of the previously connected nodes. If the ‘current’ node has both the left and right child, connect them with each other and with the previously connected nodes. Otherwise, if the ‘current’ node has only the left child or the right child, connect it with the previously connected nodes. Return the next level head after connecting each level.

Serialize/Deserialize Binary Tree

Serialize a binary tree to a file and then deserialize it back to a tree so that the original and the deserialized trees are identical.
Serialize: write the tree in a file.
Deserialize: read from a file and reconstruct the tree in memory.
Runtime Complexity: Linear, O(n).
Memory Complexity: Logarithmic, O(logn). Recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of the binary tree h. It will be O(logn) for a balanced tree and in the worst case can be O(n).
There can be multiple approaches to serialize and deserialize the tree. One approach is to perform a depth-first traversal and serialize individual nodes to the stream. We’ll use a pre-order traversal here. We’ll also serialize some marker to represent a null pointer to help deserialize the tree.
Consider the below binary tree as an example. Markers (M*) have been added in this tree to represent null nodes. The number with each marker i.e. 1 in M1, 2 in M2, merely represents the relative position of a marker in the stream.
Connect All Siblings
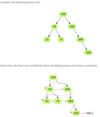
Given the root to a binary tree where each node has an additional pointer called sibling (or next), connect the sibling pointer to the next node in the same level. The last node in each level should point to the first node of the next level in the tree.
Runtime Complexity: Linear, O(n).
Memory Complexity: Constant O(1).
A binary tree is a data structure made up of nodes, where each node contains a “left” reference, a “right” reference, and a data element. The topmost node in the tree is called the root. Every node except the ‘root’ node is connected by a directed edge from exactly one other node. This node is called the parent of that node. On the other hand, each node can be connected to an arbitrary number of nodes, called children. Nodes with the same parent node are called siblings.
Each node in the above binary tree has one more pointer i.e. next along with the left and right pointers. ‘Next’ is used to connect one node to the other. After connecting siblings, a linked-list-like structure is formed whose head is the root node. We keep two pointers current and last. ‘current’ is the node we are working at and ‘last’ is the last node in the linked list already constructed (i.e. siblings already connected). Below are the steps we use to connect all siblings in the tree:
Initially set both current and last as ‘root’
while current node is not null
If current node has a left child, append this left node to the last and make it last node.
If current node has a right child, append this right node to the last and make it last node.
update current node to current’s next node

Inorder Successor BST with Parent Pointers
An inorder successor of a node in a binary tree is the next node in an inorder traversal. Write a method to find an inorder successor of a given binary tree node in a binary search tree given parent pointers.
The following BST has a parent pointer for each node. In the above tree:
- inorder successor of 25 is 50
- inorder successor of 50 is 75
- inorder successor of 75 is 100
- inorder successor of 100 is 125
- inorder successor of 125 is 200
- inorder successor of 200 is 350
- inorder successor of 350 is NULL since that’s the last node

Runtime Complexity: Logarithmic, O(logn).
Memory Complexity: Constant, O(1).
We strongly recommend that you try solving the inorder successor in BST without parent pointers first. Here is the algorithm for finding an inorder successor with parent pointers:
If the given node has a right child, then the left most child in the right child’s subtree will be the inorder successor
If the given node has no right child, then:
Start going up the parent chain. In this chain, keep going until you find a node who is a left child of its parent. This parent node will be the inorder successor
If no such node is found, the inorder successor will be NULL

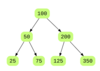
Nth Highest in BST
We are given a Binary Search Tree(BST) and a node number n. We have to find the node with the nth highest value.
Consider the following BST as an example. In this BST:
- Highest node is 350
- 2nd highest node is 200
- 3rd highest node is 125
- 4th highest node is 100
- 5th highest node is 75
Runtime Complexity: Linear, O(n). It will be O(logn) for a balanced tree and in worst can be O(n).
Memory Complexity: Linear, O(h)
The recursive solution has O(h) memory complexity as it will consume memory on the stack up to the height of binary search tree h. It will be O(logn) for a balanced tree and in worst can be O(n).
If each node in the BST has a count of total nodes in its left and right subtrees, then we can find the nth highest in a non-linear way.
The basic algorithm to find the nth highest number with counts populated in BST is as follows:
We start with the root node.
k = current node total count - count of current’s left node (i.e. number of nodes in right subtree + 1)
if k equals n then
node is the nth highest
if k is greater than n then
nth highest node exists in right subtree so find nth node in right subtree
if k is less than n then
nth highest node exists in left subtree so deduce k from n and
find (n - k)th node in the left subtree

Mirror Binary Tree Nodes
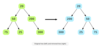
Given the root node of a binary tree, swap the ‘left’ and ‘right’ children for each node. The below example shows how the mirrored binary tree should look like.
Runtime Complexity: Linear, O(n). Every sub-tree needs to be mirrored so we visit every node once and mirror the sub-tree starting there. Hence run time complexity is O(n).
Memory Complexity: Linear, O(n) in the worst case. Recursive solution has O(h) memory complexity, for a balanced tree, as it will consume memory on the stack up to the height of the binary tree. For a skewed tree, it can be O(n).
Here, we will do a post order traversal of the binary tree. For every node, we will swap it’s left child with its right child. The original nodes are shown in green color while the nodes that have been swapped are shown in grey. The node at the top of the stack (current node) is shown in light blue. Note that we are doing DFS on the tree i.e. before returning from a node all its children have been visited (and mirrored).
Delete Zero Sum Sub-Trees
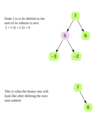
Given the root of a binary tree, delete any subtrees whose nodes sum up to zero. In the below binary tree, we need to delete the subtree starting at node 5 as it’s sum (5 -3 -2) equals zero.
Runtime Complexity: Linear, O(n).
Memory Complexity: O(h).
Recursive solution has O(h) memory complexity as it will consume memory on the stack up to height of binary tree h. It will be O(logn) for balanced tree and in the worst case can be O(n).
We will do a post order traversal of the binary tree. Before moving forward, lets discuss what post order traversal really is:
Post-order
Traverse the left subtree by recursively calling the post-order function.
Traverse the right subtree by recursively calling the post-order function.
Process the data part of the root element (or current element).
For every node, if it’s left or right subtree reports zero sum, we will delete that subtree. Moreover, if the root node returns zero then we will delete the entire tree.