Graph Strategies Flashcards
Clone a Directed Graph
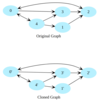
Given the root node of a directed graph, clone this graph by creating its deep copy so that the cloned graph has the same vertices and edges as the original graph.
Let’s look at the below graphs as an example. If the input graph is G = (V, E) where V is set of vertices and E is set of edges, then the output graph (cloned graph) G’ = (V’, E’) such that V = V’ and E = E’.
Linear Runtime, Linear Memory complexity
We use depth-first traversal and create a copy of each node while traversing the graph. To avoid getting stuck in cycles, we’ll use a hashtable to store each completed node and will not revisit nodes that exist in the hashtable. The hashtable key will be a node in the original graph, and its value will be the corresponding node in cloned graph.

Minimum Spanning Tree
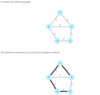
Find the minimum spanning tree of a connected, undirected graph with weighted edges.
Runtime Complexity: Quadratic, O(n2). Here, ‘n’ is the number of vertices.
Memory Complexity: Linear, O(n + e). Here, ‘n’ is the number of vertices and ‘e’ is the number of edges.
A spanning tree of a connected, undirected graph is a subgraph that is a tree and connects all the vertices together. One graph can have many different spanning trees. A graph with n vertices has a spanning tree with n-1 edges.
A weight can be assigned to each edge of the graph. The weight of a spanning tree is the sum of weights of all the edges of the spanning tree. A minimum spanning tree(MST) for a weighted, connected and undirected graph is a spanning tree with a weight less than or equal to the weight of every other spanning tree.
We’ll find the minimum spanning tree of a graph using Prim’s algorithm. This algorithm builds the tree one vertex at a time, starting from any arbitrary vertex. It adds the minimum weight edge from the tree being constructed to a vertex from the remaining vertices at each step.
The algorithm is as follows:
- Initialize the MST with an arbitrary vertex from the graph
- Find the minimum weight edge from the constructed graph to the vertices not yet added in the graph
- Add that edge and vertex to the MST
- Repeat steps 2-3 until all the vertices have been added to the MST
The time complexity to find the minimum weight edge is O(n2). However, it can be improved further by using heaps to find the minimum weight edge.
Word Chaining
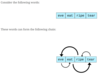
Figure out whether the given words can form a circular chain. Assume that a single word can never form a chain.
Two words can be chained together if the first word’s last letter is equal to the second word’s first letter. We are given a list of words and we need to figure out if all the words can be chained together or not. Let’s assume that all the words are lower case.
Runtime Complexity:
generate_graph: Quadratic, O(n2).
check_cycle_rec: Factorial, O(n!).
The recurrence relation for time complexity is: T(n) = O(n) + nT(n-1)
Memory Complexity: Linear, O(n). A recursive solution will consume memory on the stack as well.
A naive solution for this problem is to find all the permutations of these strings recursively, and then return true once a chain is detected. The run time for this approach will be O(n!), although, practically it will be lesser as we will prune permutations early if they are not conforming with our chaining logic.
A better solution is to do a linear pass of the word list and construct a graph that represents the start and end characters of each word. We need to add an edge from the starting character of a word to its ending character for each word in the list. If there exists a cycle in this graph containing all the nodes, then a chain can be formed.
To form a chain connecting all the strings, the graph must be connected in such a way that if we start traversing it from any vertex, it should end at the same vertex. This ensures that all vertices have been visited and all edges have been traversed exactly once, thus forming a cycle which represents the chain of words.
This leads us to the concept of an Euler circuit of a graph. An Euler circuit is a circuit that uses every edge of a graph exactly once. It starts and ends at the same vertex. Therefore, we can find that a chain exists for a list of words if there exists an Euler circuit for the graph created by them.
To find the Euler circuit of the graph, we need to ensure these two points:
The in-degree of every vertex is equal to its out-degree.
There exists a cycle connecting all the vertices of the graph which starts and ends at the same vertex.
The approach we will use is as follows:
Create Graph:
While not end-of-list
Read a word
Create a node with start char of the word (if not already created)
Create a node with end char of the word (if not already created)
Add an edge from start node to end node by adding the end node to the adjacency list of the start node
Save the start node as an in vertex of the end node
Check Cycle:
current_node = first node
if out degree of every node is equal to its in degree
Call check_cycle for current_node
Visit the node
If all nodes have been visited and starting node is adjacent to the current node,
return TRUE
Otherwise,
For all adjacent nodes of the current node
if(adjacent node has not been visited yet)
current_node = adjacent node
Call check_cycle recursively for current node
if it returns true, return TRUE, otherwise return FALSE
return FALSE
If check_cycle returns TRUE, it tells us that a chain can be formed.