Ajustements / Cotation fonctionnelle Flashcards
(19 cards)
Relation prix / intervalle de tolérance
0,3mm à 0,1mm -> On double le prix

Définition Arbre / Alésage
Alésage MAJUSCULE
Arbre minuscule

Cotation tolérancée
(CN, ES, EI, Cote maxi, Cote mini, Cote moyenne)
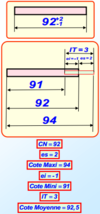
Notation des côtes tolérancées
Chiffrées :
Ecart supérieur au dessus en mm.
Nul -> pas de signe
Tolérance symétrique -> signe ±
Système ISO :
ex : 25 H 7
côte nomianle, lettre tolérance (MAJ/min), chiffre qualité de tolérance
Lire l’intervalle de tolérance pour diamètre 130mm qualité 10

IT = 160 µm
/!\ en µm, 1µm = 0,001mm
/!\ Chiffre grand = qualité mauvaise
Système ISO, lettres de position
A à Z pour alésages
a à z pour arbres
A/a -> état minimal de matière
alésage normal : H
arbre normal : h

Ajustement système ISO
ex : Ø80 H8 f7
côte nominale, alésage, arbre
< h : jeu, h/p : incertain, > h : serré
On commence toujours par l’alésage
Le jeu
jeu maxi = ES - ei
jeu mini = EI - es
- avec jeu / jeu incertain / avec serrage

Système de l’alésage normal H
Plus utilisé et facile à mettre en oeuvre.
Jeu H9e9
Incertain H7k6
Serrage H7p6

Types de conditions fonctionnelles
Jeu, retrait, réserve de filetage

Côte condition (CC)
Vecteur exprimant une exigence fonctionnelle.
Vecteur à double trait orienté positivement ⇒ ⇑
Surfaces terminales
Surfaces auxquelles se rattachent une côte-condition
(perpendiculaires à la direction de la CC)

Surfaces de liaison
Surface de contact entre les pièces assurant la CC.
(perpendiculaires à la direction de la CC)

Chaîne minimale de côte (3 règles + notation)
Chaque côte commence/termine sur la même pièce
Une seule côte par pièce
Passage d’une côte à l’autre par la surface d’appui entre 2 pièces
On nomme la chaîne ai, a nom de la CC, i n° de la pièce

Démarche pour la CC (6)
1 - Repérer les surfaces fonctionnelles
2 - Placer vecteur CC a
3 - Tracer le vecteur qui part de l’origine de a en reprenant à chaque surface de liaison rencontrée
4 - Fermer la boucle : vecteur du dernier appui à l’extrêmité de a
5 - Nommer les côtes fonctionnelles
6 - Vérifier qu’il y a une côte par pièce dans une même CC
7 - Reporter les côtes fonctionnelles sur les dessins de définition
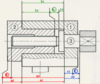
Relation vectorielle
Fermeture vectorielle de la chaîne a = a1 + a2 (/!\ flèches à ajouter !)
On a donc a = a1 - a2
amax = a1max - a2min
amin = a1min - a2max
ITa = amax - amin
ITa = ITa1 + ITa2
Choix des intervalles de tolérance
IT(a) = Somme IT(ai>N)
Pour réduire le coût de fabrication, on fixe IT(a), on cherche IT(ai) respectant la condition** IT(a) ≥ Somme IT(ai>N)**
Infinité de solutions mais une seule optimale par rapport au coût.
Choix IT : Cotation par iso intervalle
Solution simple, on prend IT(ai) ≤ IT(a)/N
/!\ Très coûteux si les côtes fonctionnelles ne sont pas proches
ex : on fixe IT(a) = 0,02
on a a1 = 300 et a2 = 5
Donc a1 = 300 ± 0,01 et a2 = 5 ± 0,01
/!\ a1 $$$ par rapport à a2 !!!
Choix IT : Cotation par iso qualité
Solution optimale : même qualité pour toutes les côtes fontionnelles
Problème complexe
Plusieurs paramètres :
- pour une meme qualité, IT varie en fct de la côte
- liaison : 1 côte intervient dans plusieurs CC (=> résolution globale)
- Parmi N cotes, certaines côtes moyennes / IT sont imposées (composants du commerce)


