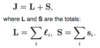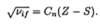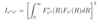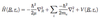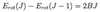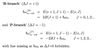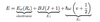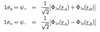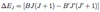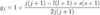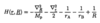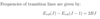Atomic

Question 1

What is meant by reduced mass?

Answer 1

• effective mass of a system once centre of mass motion is separated
  
  • 1 particle orbiting the common centre of mass

Question 2

What is meant by configuration, term and level? Give an example of each

Answer 2

• Configuration
  
  • arrangement of the occupancy of number of e-s for a given orbital
    
    • L
  • Carbon: 1s² 2s² 2p²
• Term
  
  • for a given configuration, arrangement of number of e-s are split into terms to include L and S for e-s outside closed shells & subshells
    
    • L & S
  • ¹D
• Level
  
  • for a given term, arrangement of e-s are split into levels to include J which arises from spin-orbit interaction
  • energy splitting from LS coupling
  • levels are eigenstates of J², J_z, L², S²
    
    • J, L & S
  • ⁵D₂

Question 3

State Hund’s 3 rules

Answer 3

Lowest energy when

1. For a given configuration, term with max. multiplicity 2S+1
   
   1. bigger S => lower E
2. For a given multiplicity, term with largest L
   
   1. bigger L => lower E
3. For a given term
   
   1. outer shell less than half-full
      
      1. lower J => lower E
   2. outer shell more than half-full
      
      1. bigger J => lower E
   3. half full
      
      1. no multiplet splitting (thought it was the lower J….?)

Question 4

What are the dipole allowed transitions for many electron atoms?

Consider rigorous and approximate selection rules.

Answer 4

Rigorous rules: (I changed te order so they’re now in order of strength)

• ΔJ = 0, ± 1 {J=0 => J’=0 Forbidden}
• ΔM_j = 0, ± 1 (no effect unless there is a B or E field)
• Laporte rule - parity must change

Approximate rules:

• ΔS = 0
• ΔL = 0, ± 1 {L = 0 => L’ = 0 Forbidden} (Δl = ± 1 for 1 e-)

Strong transitions:

• atomic transitions are stronger the more dipole selection rules they fulfil

Question 5

Dipole selection rule for Hydrogen.

Answer 5

Laporte rule - parity switch

Δl = ± 1

Δm = 0, ± 1

Δs = 0

If LS coupling is significant:

Δj = 0, ± 1 (but no j = 0 => j’ = 0)

Question 6

List the approximate order of strength of the dipole transitions, including those that are forbidden.

Answer 6

1. ΔS =/= 0 - Weakly forbidden (stronger transition than ΔL =/= 0, ±1)
2. ΔL =/= 0, ±1 - Forbidden (stronger than J and Laporte rule transition)
3. Laporte rule violation - strongly forbidden (weaker transition)
4. J = 0 => J’ = 0 - Most strongly forbidden (weakest transition)

Question 7

What is metastability?

Answer 7

• spontantenous decay from excited state i to all final states f is a forbidden dipole transition i.e. Ai_f ≈ 0
  
  • any transition from i this unlikely to occur
  • e- in metastable state i is trapped there

Question 8

What do the quantum numbers l, s, j, m_l, m_s, m_j represent and what values do they take?

Answer 8

These are the angular momentum quantum numbers.

• l = Orbital ang. mom; l = 0,1,2,…,n-1
  
  • gives magnitude of orb. ang. mom => l(l+1)ħ²
  • m_l = orbital. mag. mom; -l,…,l
    
    • gives component of orb. ang. mom => m_lħ
• s = spin ang. mom; s = 1/2 (fermions), 0 (bosons)
  
  • gives magnitude of spin ang. mom => s(s+1)ħ²
  • m_s = spin mag. mom; -s,…,s
    
    • gives component of spin ang. mom => m_sħ
• j = total ang. mom; j = | l - s |,…, | l + s |
  
  • gives total ang. mom. => j(j+1)ħ²
    
    • m_j = total mag. mom; -j,…,j
      
      • gives component of total ang. mom => m_jħ

Question 9

Sketching the first few spherical harmonics.

Answer 9

Question 10

Which quantum numbers are needed to completely specify the electrons state in hydrogen?

Answer 10

n, l and m

Question 11

How do n, l and m arise from geometrical constraints on the wavefunction.

Answer 11

• n - arises from the need for the radial solution to converge
  
  • => leads to energy quantisation, n is an integer.
• l - need for polar solution to converge, l is an integer.
• m - need for φ(…) = φ(…+2π), m must be an integer.

Question 12

How do we find the radial probability density (measure of finding e- at distance from the nucleus)?

Give the number of peaks for the curve of a particular (n,l) state.

Answer 12

• total probability density for the wavefunction is split into radial and angular parts - don’t forget the spherical coordinates (Jacobian gives r²)
  
  • radial probability density = integral of |R_nl(r)²| r² from 0 to infinity
    
    • spherical harmonics are normalised
• Can sketch the distribution for different quantum states in Hydrogen
• (n - l) peaks

Question 13

Using the hydrogen radial distribution curves, what is meant by “electron penetration”” and what are the consequences for the order in which orbitals are filled?

Answer 13

• Electron penetration describes degree to which e-s in diff. (n,l) states penetrate region occupied by 1s electrons
  
  • varies with l (and n, but less so)
• The more they penetrate this region, the less shielding and the more effective nuclear charge they feel.
  
  • hence more tighly bound by the nucleus
  • => have lower energy levels
• Since orbitals are filled in order of increasing energy, states with lower l are filled first
• For a given n, probability of finding e- near nucleus decreases with increasing l (further from nucleus) since centrifugal barrier pushes e- out so radius of sphere is greater

Question 14

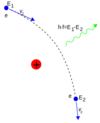
What is the Zeeman effect?

Answer 14

• splitting of spectral lines caused by energy shifts (arise from LS coupling) associated with magnetic dipole moment interacting with an external magnetic field is applied

Question 15

Describe the weak field Zeeman effect.

Answer 15

1. Normal zeeman:

• Atoms have zero net spin: closed shells/subshells
• Consider effect of only orbital angular momentum - μL
• Splitting only from interaction of L with B

2. Anomalous zeeman:

• Net spin is non-zero
• Splitting from both L and S interaction with field
  
  • => ΔE = μ_BBg_JM_J (energy shift between the level splittings)

Question 16

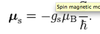
Describe the Paschen-Back case.

Answer 16

• B field is strong enough to uncouple L and S which then precess independently about the direction of the B field.
• Energy splitting now just the sum of the splitting due to L and S independently
• Can determine if field is strong by comparing it to LS splitting - if zeeman splitting is > the smallest LS splitting => strong field.
  
  • ΔE_L = μ_BBg_LM_L
    
    • gL = 1
  • ΔE_S = μ_BBg_SM_S
    
    • g_S = 2

Question 17

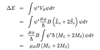
What is the Stark effect?

Answer 17

• Splitting of energy levels due to the application of an external E field.

Question 18

What is the Quadratic Stark effect?

Answer 18

• atoms with no intrinsic dipole moment
• field polarises e- density inducing dipole moment p
  
  • which is proportional to E_ext
  • so interaction energy VE = -p.E_ext = -(1/2)αE²_ext
    
    • α = dipole polarisability
  • hence varies quadratically with field
  • interaction of dipole moment with E field => energy splitting
• energy shift given by eqn
  
  • ​where A & B are level dependent constants

Question 19

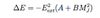
What is the linear stark effect?

Answer 19

• Atoms with intrinsic dipole moment (e.g. excited states of H & H-like atoms which have l-degeneracy)
• E field causes mixing of states with m =/=0
  
  • applied E field in z direction connects states with Δl = ±1 & Δm_l = 0
    
    • due to electric dipole selection rules
• States with m=0 are centre on x-y plane but E in z direction
• E field pulls e-s to left or right and causes a mixing eigenstates of s and p states which then experience a +ve or -ve energy shift of ΔE
• Perturbing potential does not act on states where e- distributions are concentrated in x-y plane
• eigenstates of H = H₀ + eE_extz are also eigenstates of H₀ so no work in mixing wavefns => energy is linear in E_ext
• exctied state behaves as if it had electric dipole of magnetic 3ea₀

Question 20

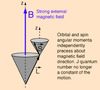
Describe the Stern-Gerlach experiment

Answer 20

• demonstrated the quantisation of e- spin in 2 orientations
• silver atoms beam in the s state placed in non-uniform B field
• atoms experience a force along B field direction
• Since mag. moment of atoms can classically point in any direction => spread expected?
• 2 beams in opp directions observed

Question 21

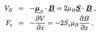
Linear stark energy diagram

Answer 21

• ψ+ ( sum of states) has e- density shifted towards -z, so mag. dipole is direction of E => ΔE < 0
• ψ- (diff. of states) has e- density shifted towards +z, so dipole antiparallel to E => ΔE > 0

Question 22

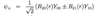
What is the quantum defect and how does it vary with the quantum numbers n and l?

Answer 22

• Quantifies departure from Hydrogenic behaviour - correction term to n.
• Alkali atom has single optically active (valence) electron
  
  • further out it is (higher l), the smaller the effective nuclear charge it feels (due to inner e-s & their shielding effects)
    
    • and the closer to a hydrogenic e- it is
• Quantum defect decreases with l and n, although more slowly with n.

Question 23

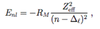
What is jj coupling?

Answer 23

• high Z atoms where spin-orbit interactions >> e-e interaction ( spin-spin or orbit-orbit interactions)
• individual orbital angular momenum combines with corresponding individual e- spin to from individual total angular momentum

Question 24

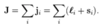
How to calculate the quantum defect

Answer 24

• Note in the original quantum defect formula, the energy represents the energy above the ground state
  
  • => this is equivalent to the energy of the particular (n,l) state subtracting the ionisation energy (ground state energy)
• Replace the E in the formula with E_nl with (E_nl - E_ion)
  
  • E_observed = E_ion + E_{nl(outer electron)}
  • => E_obs - E_ion/hc = -R_MZ_eff²/n_eff²
• Z_eff = 1 for alkali metal atoms

Question 25

What is L-S coupling (Russell-Saunders coupling)?

Answer 25

• low Z atoms when e-e interaction dominates
  
  • individual e- spin combines to form S
  • individual orbital angular momenta combines to form L
  • L & S couple to form J

Question 26

How to calculate the limit when an external B field considered to be strong?

Answer 26

• When spin orbit splitting ≈ separation of the sub-levels due to weak B field
  
  • ΔE_SO ≈ g_Jμ_BB

Question 27

What is meant by hyperfine structure?

Answer 27

• energy level splitting from coupling of net nuclear spin I and J (F = I + J)
  
  • Inclusion of net nuclear spin causes further energy perturbation besides spin-orbit coupling
    
    • interaction of net nuclear spin I with atom’s internal magnetic field

Question 28

What is Pauli exclusion principle for multielectron atoms? And what does this imply about their wavefunctions? Why can’t electrons have the same quantum numbers?

Answer 28

• e-s are fermions so each e- in multi e- atom must be described by a different spin-orbital
• total wavefns must be antisymmetric wrt exchanged of e-s
  
  • since no 2 fermions can occupy the same quantum state
• if nlm = n’l’m’ then it would not satisfy the antisymmetry of the total wavefn

Question 29

What are the 3 processes that occur when a 2 level system is in eqm with a radiation field?

Answer 29

1. Absorption
   
   1. atom absorbs photon from field & is excited to higher E state
      
      1. rate of absorption is proportional to pop. of ground state (N) & energy density U
2. Spontaneous emission
   
   1. atom decays from excited state emitting a photon
      
      1. rate of decay is proportional to excited state pop. (N₂)
3. Stimulated emission
   
   1. photon from field causes excited atom to decay and emit photon
      
      1. rate of emission proportional to excited state pop. N₂ & energy level U

Question 30

How can alkali atoms be cooled to sufficiently low temps to form Bose-Einstein condensate?

Answer 30

• To achieve cooling, atoms must be sufficiently slowed to about 1cms^-1
  
  • ^​(at room temp. atoms have velocities of several hundred ms^-1)
• atoms are bombarded with many photons with energies close to transition frequency
  
  • many since one has too little effect as p_photon << p_atoms
• atoms subjected to pair of counterpropagating (photon) laser beams
• Atoms see photons as doppler shifted
  
  • beam towards (opposite direction to) atom will be blueshifted (higher frequency)
  • beam in (same) direction of atoms motion will be redshifted (lower frequency)
• probability of scattering (absorption + re-emitting) a photon depends exponentially on how close a laser is tuned to resonance
  
  • blueshifted [v’= v_L(1-v/c)] => closer to resonance so probability increases (mainly absorbed)
  • redshifted [v’ = v_L(1-v/c)] => further from resonance so probability decreases
• Upon scattering, net momentum of p = hv_L/c transferred to atom
  
  • atom decays and emits photon causing atom to recoil
• Direction of emission random so effect of recoil averages to 0 => net momentum transfer to atoms against atoms direction of motion
• Frictional force on atoms depends on velocity (viscous damping)
  
  • faster atoms experience larger force slowing them down
  • => narrowing of momentum distribution as T decreased to around 10^-6 K
• atom trap wtih 3 lasers along each x, y, z axis, and inhomogenous B field added to confine atoms
• BEC (all atoms occupy & is described by same wavefn) formed at around 10^-7 ~ 10^-9 => requires further techniqe of evaporative cooling (letting “hotter” atoms escape)

Question 31

What is Moseley’s law? And when does the law apply?

Answer 31

• v_if = frequency of main x-ray emission line
• Z = atomic number
• S = screening constant (depends on series)
  
  • Z_eff = Z -S
  • S_K = 1
  • S_L = 7.4
• C_n = empirical constant independent of Z
• This law is used to find the frequencies of characteristic x-rays => applied in characteristic x-ray spectra

Question 32

What are the K-series, L-series and M-series? And what are the subscripts within each series?

Answer 32

Transitions form series (groups of lines) which are defined by final state of transitions n_f

• n_f = 1 => K-series
• n_f = 2 => L-series
• n_f = 3 => M-series

Within each series, Δn = n_i - n_f is denoted by subscripts

• Δn = 1 => α
• Δn = 2 => β
• Δn = 3 => γ

Question 33

What are the selection rules for vibration-rotation transitions for (ground electronic state of a heteronuclear) diatomic molecule? What frequency range do these transitions occur?

Answer 33

• Δv = ±1 (vibrational - from selection rules of harmonic oscillator)
• |J - J’| = 1 (rotational)
• Infra red frequencies

Question 34

What is the Franck-Condon principle? How does it account for relative intensities of various vibrational bands in transitions between different molecular electronic states? What is the Frank-Condon factor in terms of initial and final state wavefns?

Answer 34

• distribution of final vibrational states after transitions between molecular eelctronic states are determined by overlap of vibrational wavefns between ground and excited state (vibrational energy levels)
• transitions between vibrational states typically occur for states in which overlap is greater since transition is much faster than nuclei speed, therefore nuclei don’t move far in this time
  
  • hence smaller difference in nuclear coordinates of these states
  • so states with bigger overlaps have higher transmission probability
  • => higher intensity bands
• I = Franck-Condon Factor
  
  • v” = vibrational wavefn of lower state (final)
  • v’ = vibrational wavefn of upper state (initial)

Question 35

What are the singlet and triplet spin wavefns for a 2 e- atom? And give their symmetry

Answer 35

• state S = 0
  
  • gives M_s = 0
    
    • => singlet state
  • Antisymmetric w.r.t exchange
• S = 1
  
  • gives M_s = -1, 0, 1
    
    • => triplet state
  • Symmetric w.r.t exchange.
• spin-up × spin down cancels

Question 36

What condition does symmetry of spin part of wavefn place on spatial part of wavefn? Why is ground state of helium a spin singlet?

Answer 36

• e-s are fermions hence total wavefn is antisymmetric
  
  • if spin = antisymmetric then spatial = symmetric; vice versa
• e-s in ground state of helium have same n, l and m numbers
  
  • so the spatial part is symmetric (since the antisymmetric part is 0)
  • hence spin part has to be antisymmetric => spin singlet

Question 37

What is meant by total collision cross-section and differential cross-section in particle scattering experiments?

Answer 37

• total (σ_T): effective area (normal to direction of incidence) provided by a target to an incoming projectile
• differential: particle flux cattered by each target nucleus into solid angle dΩ divided by incoming intensity
  
  • flux = particles per unit time
  • intensity = particles per unit time per unit area = flux per unit area

Question 38

What is Beer-Lambert law?

Answer 38

• n = density
• l = length of cell
• I/I₀ = 100% - %attenuation
• σ_T = total collisional cross-section

Question 39

State the Pauli exclusion principle.

Answer 39

• Wave-functions are anti-symmetric w.r.t exchange of identical fermions
• and symmetric w.r.t exchange of identical bosons.

Question 40

Why are (L + S) odd forbidden by the Pauli exclusion principle?

Answer 40

• If L is odd => odd pairing of e-s with the same l
  
  • so there maybe an e- which doesn’t have a pair e- with the same n and l value
  • therefore under exchange, the set up is now different
  • => spatial wavefunction is antisymmetric
    
    • forces the spin part to be symmetric.
• But L+S is odd so S is even
  
  • spin wavefunction is antisymmetric
  • if both spin and spatial are antisymmetric
  • then total wavefunction is symmetric
    
    • => forbidden by Pauli

Question 41

When is the magnetic field in Zeeman effect considered strong?

Draw uncoupled LS diagram.

Answer 41

• If the splitting due to B field is bigger than the splitting due to LS coupling.

Question 42

Sketch qualitatively the main features displayed in a typical X-ray spectrum

Answer 42

Question 43

A diatomic molecule absorbs light in 3 different wavelength regions, what are the regions and the changes that give rise to the absorption of light.

Answer 43

1. Microwave - Transitions between rotational levels only
2. Infrared - Transitions between rotational and vibrational states together
3. Ultraviolet - Transitions between rotation, vibrational and electronic states. So high energy as electronic energy level differences are much greater.

Question 44

What are the steps needed to achieve laser action? Why is this not possible in a two-level system?

Answer 44

• ​2 photons from stimulated emission have same frequency (coherent)
  
  • each photon can stimulate further transitions => monochromatic waves coherent on a large scale
• stimulated emission to be dominant need population inversion
  
  • but cannot be produced in 2 level system where population of state 2 is increased until N₁ = N₂ (saturated transition so absorption & stimulated emission are equally likely but stimulated emission cannot become dominant process)
• To obtain population inversion, need at least 3-level system

1. atoms pumped with photon of frequency v₁₃
2. atoms accumulate in level 3 which spontaneously decays to level 2
3. atoms accumulate in metastable level 2
4. so levels 2 & 1 have inverted populations
5. incoming v₁₂ photons result in laser light at frequency v₁₂

Question 45

Give one example of a specific system which exhibits laser action showing how it meets requirements for laser action.

Answer 45

Ruby laser:

• Green light (550 nm) pumps Cr3+ ions in Ruby crystal (Cr3+ is impurity in Al2O3).
• Rapid (non-radiative) de-excitation to lower energy, metastable state => population inversion
• This can lase in red at 694 nm.
• Set-up requires > 50 % of ground state to be pumped ie large pumping power.
• Atoms in level 1 will absorb laser photons. This type of laser not very efficient.

Question 46

How does PEP lead to exclusion for electrons with identical quantum numbers?

Answer 46

Consider the a and b that label the wavefuction to be a given set of quantum numbers n, l, m and n’, l’, m’.

Question 47

State the Born-Oppenheimer approximation.

Answer 47

• Nuclei move much more slowly than electrons since they are much heavier => m_e/M_N << 1
• Consider the nuclei as fixed and find the reduced mass of the system of nuclei.
• For simplicity, consider also ideal diatomic molecules.

Question 48

Selection rules for rotational transitions and energy difference

Answer 48

ΔJ = ±1

(for molecules with per. dip. mom. => can be rotated by external E field)

ΔJ = 0 => Possible for non-linear molecules

Question 49

Nuclear motion

Answer 49

1. Rotation - dictated by spherical harmonics
2. Vibration - Radial eqn

Question 50

Difference in intensity of rotational transitions for covalent and Ionic molecules

Answer 50

• Ionic molecules have a permanent electric dipole moment => obey ΔJ = ±1
• Purely covalent molecules, like homonuclears, have no electric dipole moment => ΔJ = 2 forbidden transitions which are much weaker.
• Ionic molecules have much stronger rotational transition intensities

Question 51

Draw the energy level diagram and energy level spectrum for pure rotational transitions.

Answer 51

• Note that the spacing in the ENERGY SPECTRUM is 2B.

Question 52

At which frequencies do rotational transitions occur?

Answer 52

Microwave

Question 53

At which frequencies do vibration-rotational transitions occur?

Answer 53

Infrared.

Question 54

What are the selection rules for vibration-rotation transitions?

Answer 54

• v is the vibrational quantum number
• For harmonic approximation:

Δv = ±1 , |J - J’| = 1

• Δv = ±1 comes from harmonic oscillator approx., and Δv = ±2,±3,±4,.. (overtones) are much weaker transitions.

Question 55

Explain the branches that arise in rot-vib transitions.

Answer 55

Question 56

Give the total energy for an ideal diatomic molecule.

Answer 56

Question 57

When is the total energy for an ideal diatomic molecule valid for real molecules?

What causes it to become invalid?

Answer 57

• v small: harmonic approximation is best near bottom of well
• J small: centrifugal distortion tends to stretch molecule and lower rotational energy.
• Rotational constant B depends on v. Since molecules vibrate, effective bondlength =/= R_e => error when only considering rotation
• Potential V only approximately parabolic, for low v. For high v, corrections due to anharmonicity of potential needed.

Question 58

Draw the rot-vib energy level diagram and spectrum.

Where is the line at Hbar*w₀ missing?

Answer 58

• Since ΔJ = 0 is not allowed, the line at Hbar*w₀ is missing.

Question 59

Give the electronic transition selection rules

and which frequency range they occur in?

Answer 59

• Electronic transitions are always accompanied by vibrational and rotational.
• Selection rules: Δ Λ = 0, ±1 ΔS = 0, parity change g => u
• Since energy diff in electronic energy levels are much larger, transitions occur in ultraviolet.

Question 60

What are molecular orbitals and electronic spectroscopic notation?

Answer 60

• Linear combination of H₂⁺ orbitals
• Sum gives symmetric wavefunction, diff gives antisymmetric wavefunction.
• Electronic energy levels labelled by total electronic angular momentum Λ, similar to L in atoms. In the same way as with S, P, D, F,… we have for molecules Σ,

Π, Δ, Φ,…

Question 61

What are the electronic-vib-rot transition selection rules?

Answer 61

• Δv can take any value - vib energy levels
• ΔJ = 0, ±1 - rot energy levels
• Since bond length R_e can change, B (rot. constant) can also change and we don’t get evenly spaced roational spectrum lines.
• Also, since E_n, E_v >> E_J - spreads electronic-vibration frequency into band of closely spaced lines.

Question 62

How are x-ray spectra produced?

Answer 62

• Bombard high Z atoms ( make up the anode) with energetic electrons from the heated cathode which are accelerated across the potential difference V between the anode and cathode => K.E = eV

Question 63

Name 2 types of X-ray spectra

Answer 63

1. Continuous x-ray spectra
2. Characteristic x-ray spectra

Question 64

Describe the formation of continuous x-ray spectra

Answer 64

• Fast moving electrons are deflected by the coulomb field of heavy atoms
• Charged particles emit radiation when accelerated (or decelerated)
• This is continuous background radiation => Bremsstrahlung (braking radiation)
• X-rays produced
• Limiting case when electrons brought to a stand still and all energy is given up => cut off wavelength

Question 65

Describe the formation of characteristic x-ray spectra

Answer 65

• Some of the energetic electrons are able to collide with inner shell electrons with enough energy to cause ionisation of the electron.
• These electrons leave “gaps/or holes” behind which are filled by higher energy state electrons making the transition to the lower state.
• This results in the emission of characteristic x-rays

Question 66

Describe what leads to laser action.

Answer 66

• When population of level 1 state is smaller than level 2, N₁ < N₂ - Photon more likely to be absorbed.
• If level 2 more populated than 1, N₂ > N₁ photon likely to stimulate emission.
• Atoms from emission goes on to cause further stimulated emission and cascade of photons produced - LASER
• Therefore, population inversion where N₂ > N₁ is a necessary requirement of laser action.
• However, population inversion is not possible in a 2 level system.

Question 67

Describe laser action in a hypothetical 3 level system.

Answer 67

1. Atoms pumped with photons of frequency ν₁₃.
2. Atoms accumulate in level 3 which decays spontaneously to level 2.
3. Atoms accumulate in metastable level 2.
4. Levels 2 and 1 have inverted populations.
5. ν₁₂ photons result in laser light at frequency ν₁₂.

Question 68

Discuss briefly 2 main types of bonding found in diatomic molecules explaining the interaxtions that lead to this bonding.

Give an example molecule for each.

Answer 68

1. Covalent bonds - Sharing of electrons between atoms of similar electronegativity. H₂ as example.
2. Ionic bonds -Electron found predominantly close to one atom. Atoms have very diff. electronegativity. Normally occurs for alkali-halogen pairs, i.e. LiF, NaCl, etc.

Question 69

Define electron affinity and ionisation potential.

Answer 69

• Electron affinity A - Energy required to add an electron
• Ionisation I - Energy to remove an electron (binding energy of valence electron)
• Calculating cost of removing electron from alkali atom and adding it to Halogen: e.g. NaCl

I(Na) - A(Cl)

Subtract since A is the energy gained by the Chlorine atom.

Question 70

How can the bound energy levels of a hydrogen-like atom E_n = -R_infinity Z²/n² be modified to include effective nuclear charge, quantum defect and finite nuclear mass? How does quantum defect vary as a function of n and l, and why?

Answer 70

• change Z to Z_eff
  
  • Z_eff = nuclear charge + charge of inner e-s
  • since outer e- may have many e-s between it & the nucleus
• change n to n_eff = n - Δ_nl
  
  • Δ_nl is quantum defect
    
    • quantifies departure from hydrogenic behvaiour to account for shielding effects of inner e-s on nuclear attraction experienced by outer e-
• change R_infinity to R_M
  
  • nucleus no longer assumed to be infinitely heavier than the e-
• Δ_nl increases with l and n
  
  • since less nuclear attraction experienced for outer e- at high l
    
    • so more hydrogenic like
  • varies slower with n for a given l

Question 71

Explain the origins of spin orbit interaction and Zeeman effect correction terms in the Hamiltonian for an atom in a B field (in terms of interaction between magnetic dipole moment and a magnetic field). What is the effect of each of the terms on energy levels of the atom?

Answer 71

• spin orbit correction term H_LS
  
  • due to internal atomic magnetic fields
    
    • rest frame of e-, nucleus moves around it acting like an effective current loop => generates its own magnetic field
    • e- has own magnetic dipole moment due to its spin
    • magnetic field of nucleus interacts with magnetic dipole moment of e- so e- experiences a torque => energy cost depending on relative orientation of nucleus and e-
      
      • hence energy correction term corresponding to H_LS
• Zeeman effect correction term H_B
  
  • magnetic moments due to spin & orbital angular momentum interact with external B field
    
    • => potential energy V_B (perturbation due to external B field) corresponding to H_B
• effect:
  
  • LS causes splitting of terms to give levels
  • B causes further splitting of these levels

Question 72

What are the limiting cases where H_LS >> H_B and H_LS << H_B? Also which are the good quantum numbers (operators commute) in each case?

Answer 72

• H_LS much greater => LS remain coupled & external B field is weak
  
  • good quantum numbers: J, M_J, L, S
• H_B much greater => strong external B field causes LS to uncouple
  
  • good quantum numbers: L, M_L?

Question 73

Vector diagram for weak B field in Zeeman effect

Answer 73

Question 74

Calculate separations of all the components of a state given the energy separation between highest and lowest energy levels in 0 magnetic field

Answer 74

• find J values
• ΔE_max given by Lande interval rule with sum of all the separations of components J₁, J₂, …, J_n (higher Js of separations where ΔJ = 1)
  
  • ΔE_max = A(L,S) J₁ + A(L,S) J₂ + … + A(L,S) J_n
    
    • => ΔEmax = A(L,S) Σ_i J_i
    • obtain A(L,S)
• then separations of each individual component is
  
  • ΔE_i = A(L,S) J_i

Question 75

Estimate magnitude of an external magnetic field that is considered strong

Answer 75

• when energy level splitting due to weak field = that due to LS
  
  • ΔE_{weak field} = g_JM_Jμ_BB > smallest splitting (separations of components) due to LS coupling
  • ignore M_J since only considering energy separation between levels

Question 76

Which type of diatomic molecules undergo dipole-allowed vibrational transitions, and why? Give examples of these molecules

Answer 76

• heteronuclear molecules
  
  • hence have some electronic distortion and so have electric dipole moment
  • compared to linear molecules like H₂ whose displacement is 0
• e.g. HCl and CO

Question 77

Sketch Morse potential, marking D_e and R_e, also include a parabolic potential that approximates the Morse potential near potential minimum

Answer 77

• R_e = equilibrium bond length
• D_e = potential minimum (dissociation energy) = V(R_e)
• What’s D₀?

Question 78

How to tell if potential is in harmonic form (Morse potential is approximately harmonic for small displacements from R_e)?

Answer 78

• if V(R) is approximately parabolic => motion is approximately harmonic
• Taylor series expansion of V(R) about R=R_e
  
  • can neglect terms higher than quadratic
  • at minimum dV/dR (at R=R_e) = 0
  • giving the eqn (to 2nd order)

Question 79

How to calculate photon frequency between vibrational levels near bottom of potential well from spring constant of bond?

Answer 79

• ω² = k/m usually
• for bonds, replace m with μ
  
  • hence ω = sqrt (k/μ)
• remember mass of hydrogen = mass of proton
• and divide by 2π for answer in Hz unless stated to give in s^-1

Question 80

How does the spectrum of a

1. one-electron atom
2. rotating molecule
3. vibrating molecule

depends on reduced mass of the system? Which one is most sensitive to isotopic changes?

Answer 80

1. R_M correction term for R_infinity depends on μ
   
   1. E proportional to μ
2. B depends on μ
   
   1. E proportional to 1/μ
3. ω depends on μ
   1. E proportional to 1/sqrt(μ)

So rotating most sensitive to isotopic changes since E decreases rapidly for increasing μ

Question 81

Explain each of the 5 terms in the Hamiltonian for H2+ molecular ion in atomic units.

Answer 81

• 1st = sum of KE of each nuclei
• 2nd = KE of single e-
• 3rd = attraction between e- and nucleus A
• 4th = attraction between e- and nucleus B
• 5th = internuclear repulsion
  
  • 2nd to 5th terms make up electronic Hamiltonian

Question 82

What are the Schrodinger equations for electronic and nuclear motion in Born Oppenheimer approximation?

Answer 82

• terms with ∇_Rψ(r_i) do not feature in electronic Schrodinger eqn since electronic wavefn is assumed to be indt of changes in position of nuclei (nuclei positions fixed)

Question 83

Spectroscopic notation for single electron

Answer 83

Question 84

What further quantum numbers needed to completely specify state of electron in hydrogen?

Question 85

What makes a magnetic field “strong” or “weak”?

Question 86

What is the Hamiltonian for a molecule?

Answer 86

Question 87

How to calculate average rotational constant B?

Answer 87

• E_rot = BJ(J+1)
• calculate B for each transition
• and calculate the average B from those Bs

Question 88

Converting between joules and cm^-1.

Answer 88

• Divide through by hc to get cm^-1

Question 89

How do you expect the intensities of the rotational transitions in HD and HT to compare to those of rotational transitions in an ionically bound molecule, such as LiF?

Question 90

How Stark effect in n=1 ground state of hydrogen differs from that in excited states with n>1?

Answer 90

• n=1 of H (only has s state) has atoms with no intrinsic dipole moment
  
  • since H ground state is a non-degenerate state (has definite parity) & cannot possess an intrinsic electric dipole moment
  • induced dipole moment by E_ext
  • V_E = (-1/2)α(E_ext)² hence quadratic Stark effect
  • ΔE = -E²_ext(A+BM²_J)
• n>1 have atoms with intrinsic dipole moment
  
  • atoms have l-degeneracy i.e. all l levels for a given n have same energy
  • ΔE = ∓3eE_exta₀
    • new eigenstates of new H are also eigenstates of unperturbed H₀ so no WD in mixing wavefns so energy is linear in E_ext

Question 91

Electric field difference moved through to be decelerated from v_i to v_f (stark effect)

Answer 91

• The stark energy change is equal to the change in kientic energy. Equate them to find the magnitude of the electric field, dF.

Question 92

Draw an energy level diagram indicating dependence of energies of each of the four n=2 states in the presence of an applied E field along z. Label each state with its approximate wavefn expressed as Ψnlm

Question 93

Give expression of the forces acting on Stark states of H atom in an inhomogenous E field

Question 94

How to find most probable radius and mean radius of a (n,l) orbital given the wavefn?

Answer 94

• most probable radius from maximum of radial prob. distribution i.e. dPnl(r)/dr=0
  
  • Include 4π in Pnl(r)=r²|Rnl|² if wavefn is not normalised
• average radius
  
  • integrate from 0 to infinity of rP(r)dr

Question 95

What is the total number of states with same En i.e. total degeneracy wrt l and m?

Answer 95

• degeneracy wrt m is a feature of central potential (i.e. V = V(r)) which depends on |r|
  
  • hence potential has spherical symmetry
• degeneracy wrt l is characteristic of 1/r potential

Question 96

What is the Hamiltonian for N-electron atom?

Answer 96

Question 97

When does central field model make most sense?

Answer 97

• most alkali atoms
• one loosely bound outer e- which is optically active

Question 98

Why is spin singlet higher in energy than triplet state with same configuration?

Answer 98

• spin singlet e-s are closer together and experience stronger repulsion
• spin triplet keeps electrons apart (tend to avoid each other and Coulomb repulsion reduced)
• spatial separation is a result of spin orientation

Question 99

What is the exchange force?

Answer 99

• behaviour of sign dependency on orientation of e- spins
• consequence of Pauli Principle which couples spin and space states (one depends on the other)

Question 100

• Visualisation of spin-orbit coupling

Answer 100

• Orbital electron motion causes magnetic field within atom whose direction depends on L;
• Internal magnetic field causes torque on electron’s spin magnetic moment with direction determined by S;
• Torque doesn’t change magnitude of S, and reaction torque doesn’t change magnitude of L;
• Torques cause precessional motion of S and L with orientation dependent on each other;
• S and L precess about their sum J =L+S;
• Sz and Lz are not constants of motion.

Question 101

What is the energy shift due to spin-orbit interaction? What is the Lande interval rule?

Answer 101

Question 102

Total inelastic cross-section.

Answer 102

Total inelastic cross-section σ_ij gives probability (effective area) for scattering changing internal state of target from level i to level j. Change accompanied by corresponding loss in (gain of) energy by the projectile. σ_ij can be calculated from the Schr¨odinger equation.

Question 103

For a perfect gas, number of atoms/molecules per unit volume is constant=Loschmidt’s number, L = 2.69x10²⁵ (should be given)

• Q from ps: need to find n for Beer Lambert: n=(Lp)/p₀*
• _{where p = pressure they give}*
• _{p0= atomspheric pressure 10⁵}*
• Then sub what you get into Beer Lambert*

Answer 103

LOL what card, that is the card

Question 104

Question: DCS depends on, in this case, cos²(theta):

means: Intensity=Ccos²(theta) _{where C=constant}

to find constant they give you a way

e.g. we know at theta=45^o and 2x10⁹ intensity is collected.

you find C, then sum over cylindrical angles to get total beam not just at 45^o

^{insert into Beer Lambert!!!!!!}

Answer 104

no card