Back-tracking strategies

Question 1

Boggle

Given an NxN grid of characters and a dictionary, find all words which can be made from the characters in the grid and are present in the given dictionary. A word can start and end at any character in the grid. The next character must be adjacent to the previous character in any of the directions i.e. up, down, left, right and diagonal. The character at each position in the grid can be used only once while making a word.

Suppose we have a 3x3 grid and a dictionary as input. Six words can be made from the grid which are present in the dictionary. Green highlighted characters indicate that they form the word ‘eat’ in the grid which is also present in the dictionary. In the grid we start at character ‘E’, then move to upper diagonal for ‘A’ and then right to ‘T’ to make ‘EAT’.

Answer 1

Exponential O(Nⁿ) Runtime Complexity, where ‘N’ is the dimension of the grid.

The recurrence relation for time complexity is T(N)=N​²​​T(N-1)

Quadratic, O(N²) Memory Complexity, where ‘N’ is the dimension of the grid. Recursive solution will consume memory on the stack as well.

This is a backtracking problem. We start with one character in the grid and try to make as many words as possible starting with that character. We repeat the same process for all characters in the grid.

To find all the words starting with a character, we use an algorithm very similar to depth-first search. As every character from the grid can appear only once in a word, we’ll need to maintain a boolean matrix to indicate if the corresponding character in the grid is used to make this word.

We can really speed up our algorithm if we have a prefix method available for our dictionary.

Question 2

All Possible Braces

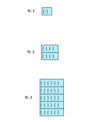
Print all braces combinations for a given value n so that they are balanced.

Here are a few examples:

Answer 2

Exponential Runtime Complexity, linear memory complexity (recursion stack).

The solution is to maintain counts of left and right braces. The basic algorithm is as follows:

left braces count: 0
right braces count: 0
if left braces count is less than n:

add left braces and recurse further
if right braces count is less than left braces count:
add right braces and recurse further
stop recursing when left and right counts are both equal to n

Question 3

Solve N-Queens Problem

Given a chess board of size N x N, determine how many ways N queens can be placed on this board so that no two queens attack each other.

Below is a valid placement of 4 queens on a 4x4 chess board, ‘X’ on the board represents a square where a queen is placed.

Answer 3

Exponential Runtime (Factorial if no Stack), Exponential Memory (recursive).

A queen can move horizontally, vertically and diagonally on a chess board. One queen can be attacked by another queen if it is present in the same row, column, or diagonal of that queen.

One very simple solution is to find all configurations with all possible placements of n-queens on the chess board and then determine for every configuration if it is valid or not. But it is very expensive, and we don’t need to do all that. It will be equivalent to choose N such configurations from NxN configurations. It is not required to try all possible configurations. We know that if we place one queen in a row, we can’t place another queen in the same row, so a lot of configurations can be easily discarded. We’ll prune unnecessary configurations and use backtracking to try another configuration.

The backtracking algorithm to solve the n-queens problem is very similar to a depth-first search of a tree. Below is the algorithm.

• Place a queen in the first column of the first row
• Now place a queen in the first such column of the 2nd row where placement is permissible i.e. the current queen is not being attacked by any queen already on the board. If no such column is found, we’ll backtrack to the previous row and try to place the queen in the next column of that row.
• We’ll continue this until we reach the last row of the board.
• When we have successfully placed a queen in the last row, that is a solution. After finding a solution, we’ll backtrack to the previous row to find the next solution. We’ll try to find another column in the previous row where placement is permissible.

We’ll use a stack to store the solution. The stack will hold only the column values and one solution will be stored in the stack at a time. When one solution is complete, we’ll backtrack using the top value from the stack and find the next solution.

Question 4

Find All K-sum Subsets

We are given a set of N positive integers and we have to find all the possible subsets of this set of integers that sum up to the number K. The following example elaborates on this further.

Answer 4

Exponential O(2n) runtime, where ‘n’ is number of integers in the given set.

Constant Memory Complexity, O(1)

n = size of given integer set
subsets_count = 2^n
for i = 0 to subsets_count
form a subset using the value of ‘i’ as following:
bits in number ‘i’ represent index of elements to choose from original set,
if a specific bit is 1 choose that number from original set and add it to current subset,
e.g. if i = 6 i.e 110 in binary means that 2nd and 3rd elements in original array need to be picked.
if subset elements sum up to K (required sum), add current subset to list of all subsets

Note that the ordering of bits for picking integers from the set does not matter i.e. picking integers from left to right would produce the same output as picking integers from right to left.