Calculus Flashcards
Definition of a derivative
Top Derivatives and Integrals
Product Rule and Quotient Rule
Inverse functions derivative rule
Inverse functions are symmetrical about the line y = x
Chain Rule Differentiation
Implicit vs. Explicit Differentiation
explicit: y = 2x
implicit: y = 2x + y2 (def of y involves y)
To solve implicit derivatives, put in (y’) where appropriate and solve for y’
example:
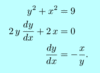
What are critical values of a derivative, and what is their importance?
Where the derivative equals zero. They can be relative/global maximums/minimums.
Use the first derivative test to determine if they are max or min.
Use the second derivative test to determine if they are concave up or concave down (which tells you max or min)
The second derivative test also tells you if a point is an inflection point or not (the 2nd derivative will equal zero).
Inflection points are where functions transition between concavity.
These tests can be applied to any order of a derivative
At what points are derivatives undefined in a function?
A cusp, a vertical tangent, and discontinuity
Mean Value Theorem
If f is continuous on the closed interval [a, b] and differentiable on the open interval (a, b), then there exists at least one number c in (a, b) such that: (view image)
Explanation: a secant line that is drawn from point a to b has a slope, m
There has to be some point, c, whose tangent line slope is also equal to m
Visual depiction of the mean value theorem
How to optimize dimensions (and other stuff) through differentiation
- Express the problem as a formula
- Determine the domain
- Find the critical numbers of the derivative
- Test the critical numbers and the endpoints of the domain for the maximum value of the original formula
What are related rates?
Example: filling up a pool with a water hose
The rate of depth in the pool is related to the rate of water out of the hose
The key is to set up an equaiton, then differentiate both sides, then solve implicitly to get your desired rate
How to use linear approximation at a point
Find the slope (through the derivative)
plug into:
y - y1 = m (x - x1)
Gives you a line to process local approximations
m is the same as f ’ (x)
What is the meaning of “marginal” in these cases: marginal cost, marginal revenue, marginal profit
The increase or decrease per 1 unit over (x + 1)
Linear approximation works great for this
Left, Right, and Midpoint area calculation formulas (All are considered Riemann sums)
n is the number of rectangles, (b-a)/n is the width of each triangle, function values are the height of each rectangle
Summation Notation
Definition of an integral
Where delta x is the withd of the ith rectangle and xi is the x-coordinate of the point where the ith rectangle touches f(x)
Another way to calculate the area under a curve that isn’t Reimann sums is the trapezoid rule
The trapezoid rule is basically the average of the left and right reimann sums
Where n is the number of trapexoids, x0 equals a, and x1 through xn are the equally-spaces x-coordinates of the right edges of trapezoids 1 through n
Simpson’s rule for calculating the area under a curve
The most accurate against the riemann sums and the trapezoid sums.
Bassically, its an average of the midpoint sum counted twice, and the trapezoid sum.
n is twice the number of “trapezoids” and x0 ans xn are the n + 1 evenly spaced points from a to b
Each “trapezoid” spans two intervals instead of one; in other words, “trapezoid” number 1 goes from x0 to x2 “trapezoid” 2 goes from x2 to x4. Because of this, the total span must always be divided into an even number of intervals
When calculating, multiply the outside term of the brackets by each inside the brackets
Fundamental Theorem of Calculus
Substitution Method for integration
It’s so natural in your mind, it seems pointless when you read the explanation
Integration by parts
The Mean Value Theorem for Integrals
Useful for finding the average value of the funciton over a particular interval
f(c) is the average value of f(x) over the interval [a, b]
How to find the area between two curves
Find the two intersection points.
Evaluate the top function’s integral over that interval.
Evaluate the bottom function’s integral over that interval.
Find the difference. That difference equals the area between the curves.
How to find the volume of weird shapes using integration
- Find the area of a normal “slice”
- Tack on the “dx” to the equation for the area
- Integrate that whole expression over the desired interval = volume
This method can be used to solve the difference in volumes of two shapes as well
Good test: Find the volume of the solid bounded by x = 2, x = 3, and y = ex. Rotated around the y-axis. Answer: 206.
Explanation: Each “slice” is 2*pi*x * ex (think wrapper around can). Add the “slices” from radii 2 to 3
How to calculate the arc length of a curve with an integral
How to find the surface area of a shape created through revolutions
Take the tiny cylinder wrapper area, integrate it over the desired axis
Notice the expression for arclength is included
How to simplify constants within an integral
Remember you can take the constant outside of the integral
L’Hôpital’s Rule
Great shortcut for doing limit problems
Let f and g be differentiable functions. If the limit of (f (x) / g (x)) must be 0/0 or infinity / infinity for this to apply. Call this “indeterminate.” The limit will equal this:
For limits, what are some unacceptable forms
+ / - infinity * 0
infinity - infinity
1 + / - infinity
00
infinity 0
For the last three cases, you can use the natural log trick:
Set the limit to “y” , then take the natural log of both sides until you can get it to an acceptable condition of L’Hospital’s rule, then solve for y.
What makes a definite integral improper
If they go infinitely up, down, right, or left and can’t be calculated
Special notes about determining area for improper integrals that have vertical asymptotes
Some you can, some just go to infinite… Here’s how you do it
Overall, you need to durn the definite integral into a limit
The first improper integral diverges, the second integral converges (there is an actual finite number as the answer)
These examples are ones where the vertical asymptotes are at the limits of integration. If the vertical asymptote is in between the limits of integration, you need to split it up into two separate limits about the undefined point. Be sure one limit is evaluated from the left, and the other limit is evaluated from the right. If any component of this divided integral diverges, the original whole version diverges.
Another way for improper integrals to converge or diverge
Besides having vertical asymptotes, improper integrals can diverge or converge from infinty set as one of the limits of integration
(The example converges)
If both of the limits of integration are negative infinity and positive infinity, then split it up into two integrals at 0 and solve. Doesn’t have to be 0…
Difference between a sequence and a series
Series is sum of the terms
What does it mean for a sequence to converge
The sequence approaches a finite term as n approaches infinity.
If it doesn’t, it’s considered divergent. This happens when the sequence increases forever, oscillates, or has no pattern at all
Using L’Hopital’s rule with sequences
Use the rule twice over (find the 2nd derivative of the numerator and denominator). Evaluate the limit at infinity, and it will show you where the sequence will converge, if at all.
What are partial sums of an infinite series
A lot of times you’re asked to find the limit of the partial sums (as their own sequence)
What’s special about a sequence of partial sums
Every series and its related sequence of partial sums are either both convergent or both divergent, moreover, if they’re both convergent, it’s to the same number
Divergence test example
If the individual terms of a series do not converge to zero, then the series must diverge
P-series rule
Telescoping series rule
The sum ends up being 1 + 1 / (n + 1)
Which is either some number between 1 and 0, or 1
Limit comparison test
Direct comparison test
This tells you nothing if the series is bigger than a known convergent series or smaller than a known divergent series
Integral Comparison test
Basically, if you can integrate the series expression, do so, and see if the integral converges or diverges
Ratio test
The ratio of a geometric series has to be less than 1 to converge
Root test of a series
How to integrate difficult polynomial expressions
Do partial fraction expansion, and integrate each individual part
Alternating series: absolute vs. conditional convergence
Alternating series change signs every term. If left alone, and if the series converges, the series is said to be conditionally convergent. If all the terms were made into the same sign, and the series was still convergent, then the series would be called absolutely convergent
The alternating series test
The nth term test for series divergence
Keeping all the series tests straight
10 tests mentioned total
Geometric series, p-series, and telescoping series. A geometric series convergesif r is between 0 and 1. A p-series converges if p > 1. A telescoping series converges if the second “half term” converges to a finite number.
Comparison tests: direct comparison, limit comparison, and integral comparison tests. All three compare a new series to a known benchmark. If the benchmark converges, so does the series you’re investigating; if the benchmark diverges, so does your new series.
Two “R” tests. Ratio and root. No benchmark comparison, Both involve taking a limit, and the results are analyzed. If the limit is less than 1, the series converges; if the limit is greater than 1, the series diverges, and if the limit equals 1, the test is inconclusive.
The nth term test of divergence and the alternating series test.
Taylor series wordy explanation
The taylor series is a specific form of the power series. It can be thought of a polynomial with an infinite number of terms. The interval of convergence of a power series is the interval of x values that will converge to a number.
The Maclaurin series is a simplified version of the Taylor series.
Format of a power series
Power series general form
Centered around “a”
Properties of the interval of convergence
Every power series converges for some value of x. The interval is never an empty set
Use the ratio test to determine if so (taking limits)
Maclaurin Series
- Find the first few derivatives of the function until you recognize a pattern
- Substitute 0 for x into each of these derivatives
- Plug these values, term by term, into the formula for the Maclaurin series.
- If possible, express the series in sigma notation
Taylor Series
