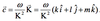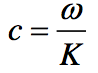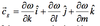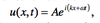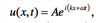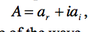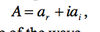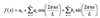Chapter 1 Flashcards
…………………. support many wavelike motions
The governing equations
waves are broadly defined as
oscillations of the dependent variables
Some of the waves supported by the equations are:
- External (surface) gravity waves
- Internal gravity waves
- Inertia-gravity waves
- Acoustic waves (including Lamb waves)
- Rossby waves
- Kelvin waves
- Kelvin-Helmholtz waves
Some of these waves are important for the
dynamics of synoptic scale systems
Some of these waves are important for the dynamics of synoptic scale systems, while others are merely
noise
In order to understand dynamic meteorology, we must understand
the waves that can occur in the atmosphere.
what are the governing equations?
set of equations that controls processes in the atmosphere
ex: momentum
what does a wave mean? (particles)
particles are not moving (stationary)
- long wave (look like oscillation)
- wide wave (ring)
what is the difference between oscillations and waves?
oscillations
- No wavelength
- can be part of the wave
sin and cosine can be applied to both
whenever you see sin and cosine think of
waves
define amplitude
half of the difference in height between a crest and a trough
define wavelength
(,) – the distance between crests (or troughs)
define wavenumber
K= 2pi/lamda
the number of radians in a unit distance in the direction of wave propagation. (sometimes the wave number is just defined as 1/lamda, in which case it is the number of wavelengths per unit distance.)
A higher wave number means
a shorter wavelength.
units of wavenumber
Units are radians m-1, or sometimes written as just m-1
We can also define wave numbers along each of the axes.
- k is the wave number in the x-direction (k = 2pi/,<sub>x</sub>).
- l is the wave number in the y-direction (l = 2pi/,\y).
- m is the wave number in the z-direction. (m = 2pi/,\z).
The wave number vector is given by
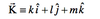
define angular frequency
(w) 2 pi times the number of crests passing a point in a unit of time.
angular frequency units
radians s-1, sometimes just written as s-1.
define phase speed
(c) the speed of an individual crest or trough.
phase speed for a wave traveling solely in the x-direction
c = w/k.
phase speed for a wave traveling solely in the y-direction
c = w/l.
phase speed for a wave traveling solely in the z-direction
c = w /m
phase speed for wave traveling in an arbitrary direction
c = w /K, where K is the
total wave number given by K2= k2+ l2+ m2
For a wave traveling in an arbitrary direction, there is a
phase speed along each axis, given by cx = w/k, cy = w/l, and cz = w/m. Note that these are not the components of a vector!
The phase velocity vector is actually given by
The magnitude of the phase velocity (the phase speed) is given by
group velocity
(cg) the velocity at which the wave energy moves
group velocity components are given by
The magnitude of the group velocity (……………….) is given by
the group speed
define frequency
number of waves passing through a unit time
f=1/T
unit s-1 or HZ
define period
he time needed for one complete cycle of vibration to pass a given point.
As the frequency of a wave increases, the time period of the wave
decreases.
define dispersion relation
an equation that gives the angular frequency of the wave as a function of wave number and physical parameters,
w=F(k, l, m, physical parameters)
Each wave type has a
dispersion relation
One of our main goals when studying waves is to determine
the dispersion relation.
Wave dispersion
1.
2.
- Dispersion wave
- non dispersive wave
when are the waves non dispersive
if the group velocity is the same as the phase speed of the individual waves making up the packet
if waves are non-dispersive then
the shape of the wave packet never changes in time
when are the waves dispersive
if the group velocity is different than the phase speed on the waves making up the packet
if the waves are dispersive then
the shape of the wave packet will change with time
waves are dispersive if
the phase velocity is not equal to the group velocity
waves are non dispersive
if the phase velocity is equal to the group velocity
expression of wave by wave number and angular frequency in x- direction with time
expression of wave by wave number and phase speed in x- direction with time
Eulerian formula
what is the difference between even function and odd function
apply the even and odd function in the eulerian formula
express sin (t) and cos(t)
Using Euler’s formula a wave traveling in the positive x-direction can be written as
a wave traveling in the negative x-direction can be written as
where the amplitude A
and gives information about
the phase of the wave
We will frequently use this complex notation for waves because it
makes differentiation more straightforward because you don’t have to remember whether or not to change the sign (as you do when differentiating sine and cosine functions).
Spectral analysis is
working with wave in the frequency domain instead of the time domain
It is rare to find a wave of a single wavelength in the atmosphere. Instead, there are
many waves of different wavelengths superimposed on one another.
t is rare to find a wave of a single wavelength in the atmosphere. Instead, there are many waves of different wavelengths superimposed on one another. However, we can use the concept of spectral analysis to
isolate and study individual waves, recognizing that we can later sum them up if need be
So, keep in mind that real atmospheric disturbances are
a collection of many individual waves of differing wavelengths.
A fourier series is
a way to represent a function as the sum of simple sine waves.
A fourier series is a way to represent a function as the sum of simple sine waves. more formally, it (what does it do?)
decomposes any periodic function or periodic signal into the sum of a (possibly infinte) set of simple oscillating functions, namely sine and cosine (or equivalently, complex exponentials)
Most continuous periodic functions (period = L) can be represented by
an infinite sum of sine and cosine functions as
the Fourier coefficients are given by
The Fourier coefficients give
the amplitudes of the various sine and cosine waves needed to replicate the original function.
The coefficient a0 is
just the average of the function
The coefficients an are the
coefficients of the cosine waves (the even part of the function).
The coefficients bn are
the coefficients of the sine waves (the odd part of the function).
Smoother functions require
fewer waves to recreate, and have fewer higher frequency components.
Sharper functions require
more waves to recreate, and have more higher frequency components.
Broad functions require
fewer waves to recreate, and have fewer higher frequency components.
Narrow functions require
more waves to recreate, and have more higher frequency components.
In general, the narrower the function, the
broader the spectrum, and vice versa.
