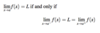Chapter 2 Flashcards
(15 cards)
Slope-Intercept Form
y = mx + b
Slope (m)
Rise / Run
y2-y1/x2-x1
Point-Slope Form
y - y1 = m(x-x1)
What happens to the slope of the secant line as b approaches a?
It approaches the slope of the tangent line
msec –> mtan
What is a secant line?
A straight line joining two points on a function.
What does the secant line represent?
The average rate of change of a function between two points.
Average Velocity =
Total Distance / Total Time
Change in distance over time
Instantaneous Velocity
Velocity at a specific time
Definition of a Limit
Suppose f(x) is defined when x is near the number a (This means that f is defined on some open interval that contains a, except possibly a itself.)
The limit of f(x), as x approaches a equals L if we can make the value of f(x) arbitrarily close to L by taking x to be sufficiently close to a (on either side of a) but not equal to a
Basic Limit Formula

What are the two ways to estimate a limit?
- Evaluate f(x) at points near a.
- Trace the graph and see y values
When are cases when a limit does not exist?
- Oscillating functions
- When the value of L is different on two sides
L is a unique value
Definition of a Left-Handed Limit
The left-handed limit of f(x) as x approaches a (or the limit of f(x) as x approxhes a from the left) is equal to L if we can make the values of f(x) arbitrarily close to L by taking x to be sufficiently close to a and x less than a.

Definition of a Right-Sided Limit
The right-hand limit of f(x) as x approxhes a (or the limit of f(x) as x approaches a from the right) is equal to L if we can make the values of f(x) arbitrarily close to L by taking x to be sufficiently close to a and x greater than a.

Limit Theorem