Chapter 2: Metric Spaces

Question 1

What is a metric space?

Answer 1

a set M and a distinace metric d that’s

* symmetric

* definite

* triangle

Question 2

What’s an open ball?

Answer 2

B(a; r) is

{x in M | d(a, x) < r}

“points less than r distance from a”

Question 3

a set E is open if…

Answer 3

for each point in E, there is a ball around the point

entirely contained in E

Question 4

U closed is closed, true?

Answer 4

No,

only interesection of closed

are closed

(or finite unions)

Question 5

E⁰ the interior of E

Answer 5

all points not on the boundary of E

or

U open sets in E

(or largest open set contained in E)

Question 6

the closure of E

Answer 6

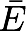
E U limit points

alternate: intersection of closed sets containing E

Question 7

What can we say about Compactness

and subspaces/superspaces?

Answer 7

compact in one means

compact in the other!

Question 8

a set A is Closed/Open

in subspace (S, d)

iff

Answer 8

there is set A* in M such that

A = A* n S

where A* is closed/open

Question 9

What’s an alternate def of Cauchy?

Answer 9

For any subsequences xni, xnj,

lim d(xni, xnj) = 0

Question 10

“Sheep Lemma”

Answer 10

For a_n Cauchy, if some subseq a_i –> a,

then a_n –> a

Question 11

Preimages f^-1 preserve

Answer 11

U, complements, and intersections

(f only preserves unions)

Question 12

Definitions of continuity?

Answer 12

• epsilon
• f^-1(open) is open
• if a_n –> a, then f(a_n) = f(a)

Question 13

Continuous images preserve

Answer 13

compactness

(not open/closed)

Question 14

What does sequentially compact mean?

Answer 14

every sequence has a

convergent subsequence

Question 15

Sequentially compact

iff

Answer 15

compact

Question 16

a totally bounded set

Answer 16

is a set A covered by finitely many

open balls in A of radius epsilon

Question 17

What is an open cover?

Answer 17

a collection of open sets

(possibly infinite)

Question 18

Heine-Borel

Answer 18

In Rⁿ,

compact

means closed and bounded

Question 19

Bolzano-Weirstrauss

Answer 19

In Rⁿ, every bounded sequence

has a convergent subsequence

Question 20

K is compact

iff

what about accumulation points?

Answer 20

every infinite subset

has an accumulation point in K

“Bolzano-Weirstrauss Property”

Question 21

A’ the derived set of A is…

Answer 21

set of accumulation points

Question 22

How do we know d(x, E) is continuous?

Answer 22

b/c

d(x, E) - d(y, E) | ≤ d(x, y)

Question 23

Lebesgue Covering Lemma

Answer 23

O an open cover of K (compact)

Lemma says

there exists r > 0, such that for any x in K,

B(x, r) is in some open set of O

“key: r doesn’t depend on the point

Question 24

Continuous on a compact set

implies….

Answer 24

uniformly continuous

Question 25

Connected

iff

about two-valued functions…

Answer 25

every two-valued function (these are continuous)

is constant

Question 26

Intervals in R, even with ∞ are…

Answer 26

connected

use IVT and two-valued function

to show contradiction

Question 27

U connected is connected if…

Answer 27

intersection is nontrivial

Question 28

What is a component of a space?

Answer 28

a connected set A such that

no other connected set contains A

Question 29

What are nice properties of components?

Answer 29

• every point is in a unique component
• components are disjoint (or the same)

Question 30

closed

iff

what about limit points?

Answer 30

contained in the set

Question 31

What is a path?

Answer 31

It’s a continuous function from [0, 1] to M

* domain uses | | metric

Question 32

path connected implies…

Answer 32

connected

but not the inverse!

Question 33

a is connected to b

“a ~ b”

Answer 33

if there is cont f on [0, 1]

such that f(0) = a and f(1) = b

Question 34

a closed interval in C is….

Answer 34

[z, w]

=

{ (1-t) z + t w | 0 ≤ t ≤ 1 }

Question 35

a convex set in C is…

Answer 35

a set such that any interval with endpoints

in the set

is entirely contained in the set

Question 36

what is a polygonal path?

Answer 36

a path whose image is

U [z_i , z_i+1]

for i = 1 to n

Question 37

Open and connected implies…

Answer 37

there is a polygonal path between any two points

Question 38

What is a characterization of

f differentiable at p?

Answer 38

there exists f* such that

1. f(z) - f(p) = f*(z) (z - p)

for some z

2. f* is cont at p

Question 39

Weirstrauss M-Test

Answer 39

If |fn| < Mn and ∑ Mn < ∞, then

∑ fn converges uniformly

(and if each fn is cont, then converge f cont.)

Question 40

fn —> f uniformly means…

Answer 40

for all n > N and any x,

fn(x) is close to f(x)

Question 41

Power series converges to a continuous func when?

Answer 41

on z < |z0|

where z0 is some point where series converges

to a number

(sup of all z0 is the radius of convergence)

Question 42

Show a space is connected

using “induction”

Answer 42

Need subset E such that

• E open (nonempty)
• for all x in E^c, B(x, r) n E is empty

“don’t even need E to be connected!”

Question 43

Equivalent ways ot thinking about

K compact?

Answer 43

• K has BWZ property
• sequentially compact
• totally bounded & complete

“BWZ” every infinite subset has a limit point in set

“totally bounded” for all e, K covered by finitely many balls

of radius epsilon (same balls)