Chapter 2: Statistics Revisited

Question 1

• What is inferential statistics?
• Why is the Normal Distribution so important?
• What is an i.i.d random sample?
• How does sample size impact the confidence interval? What is a paired t-test?
• What is the OLS estimator all about?

Question 2

What is descriptive statistics and inferential statistics?

Answer 2

Descriptive statistics can be used to summarize the data, either numerically or graphically, to describe the sample (e.g., mean and standard deviation). Taken from all data

for randomness and drawing inferences about the larger population.

Sample

Inferential statistics is used to model patterns in the data, accounting for randomness and drawing inferences about the larger population. Taken from a sample

These inferences may take the form of:

• estimates of numerical characteristics (estimation)
• answers to yes/no questions (hypothesis testing),
• forecasting of future observations (forecasting),
• descriptions of association (correlation), or
• modeling of relationships (regression).

Data Mining is sometimes referred to as exploratory statistics generating new hypotheses.

Question 3

What are random variables?

Answer 3

𝑋 is a random variable if it represents a random draw from some population, and is associated with a probability distribution.

• a discrete random variable can take on only selected values (e.g., Binomial or Poisson distributed), Person height
• a continuous random variable can take on any value in a real interval (e. g., uniform, Normal or Chi-Square distributions) 0-180 Grad

For example, a Normal distribution, with mean 𝜇 and variance 𝜎2 is written as 𝑁(μ, σ²) has a pdf of

f(x) = (1 / σ sqrt(2π)^e)^{-(x-μ)^2/2σ^2}

Question 4

The Standard Normal

Answer 4

Any random variable can be “standardized” by subtracting the mean, 𝜇, and dividing by the standard deviation, 𝜎 , so
𝐸𝑍 =0,𝑉𝑎𝑟𝑍 =1.

Thus, the standard normal, 𝑁 0,1 , has probability density function (pdf):

Question 5

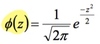
Statistical Estimation

Answer 5

Populiation with parameters -every member of the population has the same chance to be selected-> Random sample

Random sample -estimation-> Population

Question 6

Expected Value of X: Population Mean E(X)

Answer 6

• The expected value is a probability weighted average of 𝑋
• 𝐸(𝑋) is the mean or expected value of the distribution of 𝑋, denoted by u_𝑥
• Let 𝑓(𝑥_𝑖) be the (discrete) probability that X = 𝑥_𝑖, then
  
  • u_x= 𝐸(𝑋)=(n bis i=1)Σx_i f(x_i)
• Law of large numbers: the average of the results obtained from a large number of trials should be close to the expected value, and will tend to become closer as more trials are performed.

Question 7

Sampling Distribution of the Mean

Answer 7

• We can say something about the distribution of sample statistics (such as the sample mean)
• The sample mean is a random variable, and consequently it has its own distribution and variance
• The distribution of sample means for different samples of a population is centered on the population mean
• The mean of the sample means is equal to the population mean
• If the population is normally distributed or when the sample size is large, sample means are distributed normally

Question 8

Examples of Estimators

Answer 8

• Suppose we want to estimate the population mean
• Suppose we use the formula for 𝐸(𝑋), but substitute 1/𝑛 for 𝑓(𝑥𝑖) as the probability weight since each point has an equal chance of being included in the sample, then we can calculate the sample mean:
• 𝑋 describes the random variable for the arithmetic mean of the sample, while 𝑥 is the mean of a particular realization of a sample.

Question 9

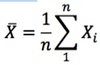
Estimators should be Unbiased

Answer 9

An estimator (e.g., the arithmetic sample mean) is a statistic (a function of the observable sample data) that is used to estimate an unknown population parameter (e.g., the expected value)

Question 10

Standard Error of the Mean: Standard Deviation of Sample Means

Answer 10

The standard deviation of the sample means is equal to the standard deviation of the population divided by the square root of the sample size.

σ / sqrt(n)

Rule:Var[aX + b] a² Var[X]

Question 11

Random Samples and Sampling

Answer 11

• For a random variable 𝑋, repeated draws from the same population can be labeled as 𝑋1, 𝑋2, . . . , 𝑋𝑛
• If every combination of 𝑛 sample points has an equal chance of being selected, this is a random sample
• A random sample is a set of independent, identically distributed (i.i.d) random variables

Question 12

Central Limit Theorem

Answer 12

• The central limit theorem states that the standardized average of any population of i.i.d. random variables 𝑋_𝑖 with mean 𝜇_𝑋 and variance 𝜎² is asymptotically ^_~𝑁(0,1), or
• Asymptotic Normality implies that 𝑃(𝑍 < 𝑧) Φ(𝑧) as
  𝑛 –> unendlich , 𝑜𝑟 𝑃(𝑍 < 𝑧) ≈ Φ(𝑧)
• In other words:
• 𝑋₁, … , 𝑋_𝑛 be 𝑛 i.i.d. random variables with mean μ and standard deviation σ.
• If 𝑛 is sufficiently large, the sample mean X is approximately
  
  • Normal with mean μ and standard deviation 𝜎/√𝑛
    
    • i.e., the mean of the sample means is equal to the population mean
    • i.e., the standard deviation of the sample means is equal to the standard deviation of the population divided by the square root of the sample size

Question 13

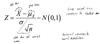
Statistical Estimation

Answer 13

• Population with mean: μ= ? –>
• A simple random sample of 𝑛 elements is selected from the population. –>
• The sample data provide a value for the sample mean 𝑥 –>
• The value of 𝑥 is used to make inferences about the value of μ.

Question 14

Student‘s t-Distribution

Answer 14

• When the population standard deviation is not known, or when the sample size is small, the Student‘s t-distribution should be used
• This distribution is similar to the Normal distribution, but more spread out for small samples
• The formula for standardizing the distribution of sample means to the t-distribution is similar, except that the sample standard deviation 𝒔 is used

Question 15

Student t-Distribution

Answer 15

Question 16

Statistical Estimation (Types)

Answer 16

• Point estimate
  
  • sample mean
  • sample proportion
• Point estimate
  • sample mean
  • sample proportion
• Point estimate is always within the interval estimate

Question 17

Confidence Interval (CI)

Answer 17

Provide us with a range of values that we believe, with a given level of confidence, contains a population parameter CI for the population means:

Pr(X - 1.96SD <= µ <= X + 1.96SD) = 0.95

lower bound and upper bound.

There is a 95% chance that your interval contains 𝜇.

Question 18

Example: Standard Normal Distribution

Answer 18

Suppose sample of 𝑛=100 persons mean = 215, standard deviation = 20

95% CI = X +- 1.96s / sqrt(n)

• Lower Limit: 215 – 1.96*20/10
• Upper Limit: 215 + 1.96*20/10
• = (211, 219)

“We are 95% confident that the interval 211-219 contains 𝜇”

Question 19

Effect of Sample Size

Answer 19

Suppose we had only 10 observations What happens to the confidence interval?

X +- 1.96s / sqrt(n)

• For n = 100, 215 1.96(20) / 100 (211,219)
• For n = 10, 215 1.96(20) / 10 (203,227)
• Larger sample size = smaller interval

Question 20

Suppose we use a 90% interval
What happens to the confidence interval?

Answer 20

X +- 1.645s / sqrt(n)

90%: 215 1.645(20) / sqrt(100) = (212,218)

Lower confidence level = smaller interval (A 99% interval would use 2.58 as multiplier and the interval would be larger)

Question 21

Effect of Standard Deviation

Answer 21

Suppose we had a SD of 40 (instead of 20) What happens to the confidence interval?

X 1.96s/ sqrt(n)
215 +- 1.96(40)/ sqrt(100) = (207,223)

More variation = larger interval

Question 22

Statistical Inference

Answer 22

1. Formulate hypothesis
2. Collect data to test hypothesis <– Systematic error
   
   1. Accept hypothesis
   2. Reject hypothesis

Random error (chance) can be controlled by statistical significance or by confidence interval

Question 23

Hypothesis Testing

Answer 23

• State null and alternative hypothesis (H_o and H_a)
  
  • H_o usually a statement of no effect or no difference between groups
• Choose α level (related to confidence level) } how much do
  
  • Probability of falsely rejecting H_o (Type I error), typically 0.05 or 0.01
• Calculate test statistic, find p-value (p)
  
  • Measures how far data are from what you expect under null hypothesis
• State conclusion:
  
  • 𝑝 ≤ 𝛼, reject H_o
  • 𝑝 > 𝛼, insufficient evidence to reject H_o

Question 24

Possible Results of Tests

Answer 24

• Null true and Reject Null = Type I (alpha error)
• Null true and Fail to reject Null = Correct
• Null false and Reject Null = Correct
• Null false and Fail to reject Null = Type II error (ß)

Question 25

Hypothesis Testing

Answer 25

Hypothesis: A statement about parameters of population or of a model (𝜇 = 200 ?)

Test: Does the data agree with the hypothesis? (sample mean 220)

Simple random sample from a normal population (or n large enough for CLT)

Ho: 𝜇 = 𝜇𝑜
Ha : 𝜇 ≠ 𝜇𝑜 , pick 𝛼

Question 26

Z-Test

Answer 26

• Der Einstichproben-t-Test (auch Einfacher t-Test; engl. One-sample t-Test) prüft anhand des Mittelwertes einer Stichprobe, ob der Mittelwert einer Grundgesamtheit sich von einem vorgegebenen Sollwert unterscheidet. Dabei wird vorausgesetzt, dass die Daten der Stichprobe einer normalverteilten Grundgesamtheit entstammen bzw. es einen genügend großen Stichprobenumfang gibt, so dass der zentrale Grenzwertsatz erfüllt ist.
• Der Zweistichproben-t-Test (auch Doppelter t-Test; engl. Two-sample t-Test) prüft anhand der Mittelwerte zweier unabhängiger Stichproben, wie sich die Mittelwerte zweier Grundgesamtheiten zueinander verhalten. Dabei wird vorausgesetzt, dass die Daten der Stichproben einer normalverteilten Grundgesamtheit entstammen bzw. es genügend große Stichprobenumfänge gibt, so dass der zentrale Grenzwertsatz erfüllt ist. Der klassische t-Test setzt voraus, dass beide Stichproben aus Grundgesamtheiten mit gleicher Varianz entstammen. Der Welch-Test oder t-Test nach Satterthwaite ist eine Variante, die die Gleichheit der Varianzen nicht voraussetzt.

Question 27

CI and 2-Sided Tests

Answer 27

• A level 2-sided test rejects H₀: = 𝜇₀ exactly when the value 𝜇₀ falls outside a level 1 − alpha confidence interval for.
• Calculate 1 − 𝛼 level confidence interval, then
  
  • if 0 falls within the interval, do not reject the null hypothesis, 𝑡 < 𝑡 /2
  • Otherwise, |𝑡| ≥ 𝑡 /2 =>reject the null hypothesis.

Question 28

Definition of a p-Value

Answer 28

The p-value describes the probability of having t=3.1 (or larger), given the null hypothesis. The smaller the p-value, the more unlikely the null hypothesis seems.

p-value and significance level are the same.

Question 29

Unpaired Samples - p-value

Answer 29

2 independent samples:

Does the amount of credit card debt differ between households in rural areas compared to households in urban areas?

• Population 1: All Rural Households 𝑚1
• Population 2: All Urban Households 𝑚2
• Null Hypothesis: H0 : 𝑚1 = 𝑚2
• Alternate Hypothesis: HA : 𝑚1 ≠ 𝑚2.

Population 1: All Rural Households 𝑚1

• Take random sample: n1 = X(arth mean)

Population 2: All Urban Households 𝑚2:

• Take random sample: n2 = X(arth mean)

Are the sample means consistent with H0?

Summary Rural:

• x1 = 6299
• s1 = 3412

Summary Urban:

• x2 = 7034
• s2 = 2467

Difference in means = €735 We have heteroscedasticity.

How likely is it to get a difference of €735 or greater if Ho is true? =>This probability is the p-value.

If small then reject Ho.

Question 30

Selected Statistical Tests

Answer 30

• Parametric Tests
  
  • F-test
    
    • Compares the equivalence of variances of two samples
    • Often used as a pre-test for the t-test
  • The family of t-tests
    
    • Compares two sample means or tests a single mean
• Non-parametric Tests
  
  • Wilcoxon signed-rank test
    
    • Independence of two means for 2 paired i.i.d samples, when normality cannot be assumed.
    • Mann-Whitney-U test is used for 2 independent samples
  • ANOVA
    
    • Equivalence of multiple means in case of several i.i.d samples (normally distributed)
  • Kruskal-Wallis-Test
    
    • Equivalence of multiple means in case of several i.i.d non-normally distributed samples
• Tests of the Probability Distribution
  
  • Kolmogorov-Smirnov and Chi-square test
    
    • used to determine whether two underlying probability distributions differ, or whether an underlying probability distribution differs from a hypothesized distribution