Flashcards in Chapter 3 ML estimation Deck (8)
Loading flashcards...
1
Q
Identification condition in ML estimation
A
There is no set of parameters observationally equivalent to the true set of parameters.
Inconsistency of the ML estimator can arise if the likelihood is flat arount the true value => curvature of the likelihood can be interpreted as a measure of the precision of the ML estimate
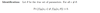
2
Q
Asymptotic distribution of ML
A
Random sampling is assumed.
- When the likelihood is well specified the information equality applies, as a result the asymptotic variance is simplified.
- The information matrix just measures the curvature of the likelihood function and as such it is a measure of the precision of the estimates
3
Q
Consistency of ML
A
- Identification condition is required.
- Random sampling also, so that LLN applies.
4
Q
Definition of MLE
A
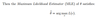
5
Q
Wald test
A
H0: h(theta)=0
H1: h(theta)<>0
- We use the unrestricted estimator.
- In the case of the ML we replace the estimator of the variance by the -1*hessian of the log-likelihood
- The result is true even for mispecified likelihoods
- Notice we just need to compute the unrestricted model
6
Q
LM test
A
Delta tilde is the maximizer of the log likelihood subject to the restriction
- Under the null, its distribution is given by the one below
- Notice for the LM test we just need to compute the restricted estimator
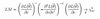
7
Q
LR test
A
Againt theta tilde is the restricted estimator
- Notice that to perform this test we have to compute both the restricted and unrestricted models
- Asymtotic distribution requires a well specified likelihood
8
Q
Nominal size
A
Supposed size of an asymptotic test different of true size of the thest
