Chapter 6 - The Normal Probability Distribution Flashcards
Variables can assume values in an uncountable set (e.g., an interval in real line).
Continuous Random Variables
A __ __ describes the probability distribution of a continuous random variable.
smooth curve
The depth or density of the probability, which varies with x, may be described by a mathematical formula f (x ), called the __ __ or__ __ __ for the random variable x.
probability distribution or probability density function
The area under the curve is equal to __.
1
P(a ≤ x ≤ b) =
area under the curve between a and b.
There is no probability attached to any single value of x. That is, P(x = a) = ?
0
Thus, P(x ≤ a) =
P(x < a)
One important continuous random variable is the __ __ __
normal random variable
Uniform Distribution The probability density function of a uniform random variable is flat:
.
Variables can assume values in an uncountable set (e.g., an interval in real line).
Continuous Random Variables
A __ __ describes the probability distribution of a continuous random variable.
smooth curve
The depth or density of the probability, which varies with x, may be described by a mathematical formula f (x ), called the __ __ or__ __ __ for the random variable x.
probability distribution or probability density function
The area under the curve is equal to __.
1
P(a ≤ x ≤ b) =
area under the curve between a and b.
There is no probability attached to any single value of x. That is, P(x = a) = ?
0
Thus, P(x ≤ a) =
P(x < a)
One important continuous random variable is the __ __ __
normal random variable
Uniform Distribution The probability density function of a uniform random variable is flat:
.
Exponential Distribution
The probability density function of an exponential random variable is:
where __ is the mean.
where µ is the mean.
__ __ variable is often used to model the lifetime of electric components
Exponential random
Survival probability:
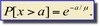
Memoryless Property:
The Normal Distribution
The formula that generates the normal probability distribution is:
To find P(a < x < b), we need to find..
the area under the appropriate normal curve.
To simpify the tabulation of these areas, we __ each value of x by expressing it as a __
Standardize
z-score
the number of standard deviations (s) it lies from the mean (m)
z-score
The Standard Normal (z) Distribution
Mean = ?; Standard deviation = ?
When x = m, z = ?
Symmetric about z = ?
Values of z to the left of center are __
Values of z to the right of center are__
Total are under the curve is __.
Mean = 0; Standard deviation = 1
When x = m, z = 0
Symmetric about z = 0
Values of z to the left of center are negative
Values of z to the right of center are positive
Total area under the curve is 1.
The four digit probability in a particular row and column of Table 3 gives the__ __ __ __ to the __ that particular value of z.
area under the z curve
left
To find an area to the left of a z-value,.
To find an area to the right of a z-value,
To find the area between two values of z,
find the area directly from the table
find the area in Table 3 and subtract from 1.
find the two areas in Table 3, and subtract one from the other.
To find an area for a normal random variable x with mean µ and standard deviation σ, __ or __ the interval in terms of __.
standardize or rescale
z
When n is large, and p is not too close to zero or one, areas under the normal curve with
mean np and variance npq
can be used to __ __ __.
approximate binomial probabilities
Make sure to include the entire rectangle for the values of x in the interval of interest. This is called the __ __.
Continuity Correction.
Approximating the Binomial
Continuity Correction
Standardize the values of x using:
We must make sure of what before approximating the binomial with normal approximation?
np > 5
nq > 5
